Файл: Курсовая работа по дисциплине Общая теория связи Разработка основных блоков цифровой системы связи.docx
Добавлен: 06.12.2023
Просмотров: 178
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица1–заданныйисходныйИКМсигнал
Итоговый ИКМ сигнал по символам:
01111 01110 01111 01011 00000 00010 10001 01010 00000 11111 00101 01010 00000 10010 00101 10000 01000 01101 00000 01110 01011 00101 00011 01110 00010 01101 00000
Или же в виде единой последовательности импульсов:
01111011100111101011011110111001111010110000000010100010101000000111110010101010000001001000101100000100001101000000111001011001010001101110000100110100000
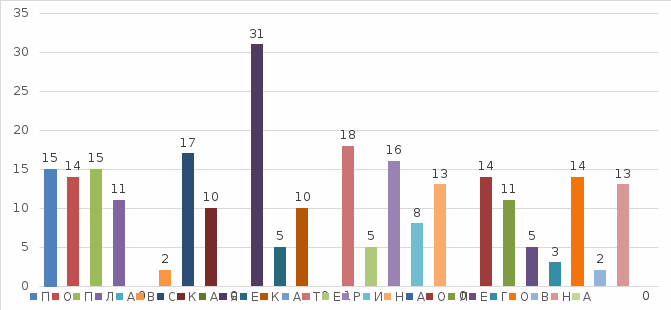
Рис.8-Квантованныйсигналпередаваемойпоследовательности
-
Рассчитать дисперсию шума
Количество букв фамилии в «Поплавская» равно 10, т.е. Umax = 10В; Количество необходимых уровней квантования L = 25 = 32; Тогда дисперсия шума 2 равна:
 2 = ????2????????????
2 = ????2????????????12(????−1)2
= 102
 12(32−1)2
12(32−1)2= 0,00867(В2)
-
Разделить сформированную в п.2 последовательность на слова из двух букв: 00,01,10,11. Получим сигнал ИКМ из п.2, разделенный на дибиты:
01.11.10.11.10.01.11.10.10.11.00.00.00.00.10.10.00.10.10.10.00.00.01.11.11.00.10.10.10.10.00.00.01.00.10.00.10.11.00.00.01.00.00.11.01.00.00.00.11.10.01.01.10.01.01.00.01.10.11.10.00.01.00.11.01.00.00.0
Предположим, что в соответствии с п.2 наш источник выдает информацию в виде случайной последовательности слов из двух букв 00, 01, 10, 11. Назовем этот исходный код—код К1. Этот код – двоичный, m=2 (1 и 0), длина кодовой комбинации n=2. Общее количество разных слов N = ????2 = 22 = 4. Между буквами в слове существуют корреляционные связи, слова – независимы.
-
Определим вероятность слов из двух букв (дибитов) 00, 01, 10, 11 в двоичной последовательности сигнала ИКМ, полученной в пункте 4. Рассчитаем
энтропию источника, т.е. кода К1, в битах на слово из двух букв и энтропию на символ (на букву). Определим избыточность источника.
Рассчитаем вероятности появления различных дибитов. Всего в передаваемой последовательности 67 дибитов. Из них дибит 00 (D0) встречается 24 раз, вероятность появления дибита (D0) равна p00=24/67=0,36, дибит 10 (D1) встречается 19 раз тогда p10=19/67=0,28, дибит 01 (D2) встречается 13 раз и p01=13/67=0,20, дибит 11 (D3) встречается 11 раз и p11=11/67=0,16. Тогда энтропия кода К1 равна:
Hсл = Н = -p(00)*log2p(00) - p(01)*log2p(01) - p(10)*log2p(10) - p(11)*log2p(11)= -
-0,36*log20,36 - 0,28*log20,28 – 0,20*log20,20 – 0,16*log20,16 = 1,93 дв.ед/слово
Энтропия:

 Н = Hсл = 1,93 = 0,97 дв.ед./букву
Н = Hсл = 1,93 = 0,97 дв.ед./буквуИзбыточность:
2
R = 1 −
2
H

Hmax
= 1 − 0,97 = 0,03
Избыточность возникла из-за наличия статистической связи между символами. Для уменьшения избыточности будем кодировать не символы, а целые слова-дибиты.
-
Закодируем сообщения кода К1 кодом К2. Для увеличения энтропии и устранения корреляционных связей кодируем не символы, а целые слова, т.е. дибиты. Код К2:
00 – кодируем символом 0; 01 – кодируем символом 1;
10 – кодируем символом 2; 11 – кодируем символом 3.
Основание кода К2 равно m = 4, длина комбинации n = 1. Энтропия кода К2 на символ равна: H p(0)*log2p(0) p(1)*log2p(1) p(2)*log2p(2) -
p(3)*log2p(3) 1,93 дв.ед./символ.
Так как p(0) = p(00); p(1) = p(01); p(2) = p(10); p(3) = p(11); то энтропия на символ кода К2 равна энтропии на слово кода К1.
Избыточность кода К2 равна:
???? = 1 −
????

????????????2????
= 1 −
1,93

2
= 0,04
Мы увеличили энтропию в 2 раза, но избыточность осталась прежней. Причины избыточности кода К2 – неравновероятность символов 0, 1, 2, 3.
-
Для уменьшения неравновероятности символов кода К2 закодируем символы кода К2 двоичным кодом К3 с префиксными свойствами, построив кодовое дерево.
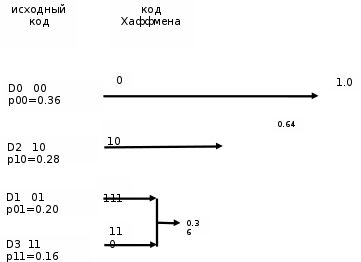




Вершина кодового
дерева
Рис.9-Построениекодовогодерева
Для кодирования сообщений идем от вершины кодового дерева к сообщению. Если в узле кодового дерева идем вверх, то в кодовую комбинацию пишем 1, а если вниз, то 0.
Таким образом имеем:
0 кодируем комбинацией "0"; 1 кодируем комбинацией "111";
2 кодируем комбинацией"10"; 3 кодируем комбинацией"110".
В результате кодирования получен неравномерный код. Наиболее вероятный символ 0 кодируется кодом минимальной длины, а наименее вероятный 3 - имеет код максимальной длины. Поэтому средняя длина комбинации кода
Хаффмена равна:
Nср = 0,36*1+0,28*2+0,20*3+0,16*3 = 2,00 бит/сообщение
После кодирования передаваемое сообщение принимает вид: Исходное сообщение в коде К2:
01.11.10.11.10.01.11.10.10.11.00.00.00.00.10.10.00.10.10.10.00.00.01.11.11.00.10.10.10.10.00.00.01.00.10.00.10.11.00.00.01.00.00.11.01.00.00.00.11.10.01.01.10.01.01.00.01.10.11.10.00.01.00.11.01.00.00.0
Закодированное сообщение кодом К3:
111.110.10.110.10.111.110.10.10.110.0.0.0.0.10.10.0.10.10.10.0.0.111.110.110.0.10.10.10.10.0.0.111.0.10.0.10.110.0.0.111.0.0.110.111.0.0.0.110.10.111.111.10.111.111.0.111.10.110.10.0.111.0.110.111.0.0.
Из 100 среднестатистических сообщений получим:
54 комбинаций "0"; 19 комбинации "10";
13 комбинаций "111"; 11 комбинаций "110". Количество "1" равно: N1 = 131 + 19 + 11*2 = 92;
Количество "0" равно: N0 = 541 + 191 + 111 = 84; Вероятность "1" равна: р(1) = 92/200 = 0,5; Вероятность "0" равна: р(0) = 84/200 = 0,5;
Энтропия кода К3 равна:
H 0,5*log20,5 0,5*log20,5 1,0 дв.ед./символ. Избыточность кода К3 равна: R 1 1,0 0.
Можно считать, что символы кода К3 равновероятен.
-
Для дальнейшего увеличения энтропии нужно закодировать дибиты кода К3 кодом К4 с основанием m = 4. Указать для кода К4 основание, энтропию, избыточность и длину комбинации.
Закодируем дибиты нового кода К3 кодом К4:
00 – кодируем символом 0; 01 – кодируем символом 1; 10 – кодируем
символом 2; 11 – кодируем символом 3.
Основание кода К4 равно m = 4, длина комбинации n = 1. Так как символы кода К3 практически равновероятны, то символы кода К4 тоже практически равновероятны. Следовательно, энтропия кода К4 максимальна и примерно равна:
H log2 m log2 4 2 дв.ед./символ.