Файл: Курсовая работа по дисциплине Общая теория связи Разработка основных блоков цифровой системы связи.docx
Добавлен: 06.12.2023
Просмотров: 180
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Избыточность же кода К4 практически нулевая.
-
Осуществить помехоустойчивое кодирование двоичных комбинаций кода К3, используя для этого код, указанный в таблице 1.
а) Задан блочный код (7,3) и строка порождающей матрицы: 0101101 Составляем порождающую матрицу G. Эта матрица должна иметь n столбцов и k строк. Левая часть матрицы – это единичная матрица размером k*k. Правая часть G – это матрица-дополнение P размером (n–k)*k. Заданная строка – верняя, т.к. начинается на 100.
| 1 | 0 | 0 . х | х | х | х |
| G = |0 | 1 | 0 . 1 | 1 | 0 | 1| |
| 0 | 0 | 1 . х | х | х | х |
Формируется матрица-дополнение Р. Она должна иметь разные столбцы и количество 1 в столбцах должно быть максимальным, возьмем такой вариант P:
| 1 | 0 | 1 | 1 |
| P = |1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 |
Тогда итоговый вид порождающей матрицы:
| 1 | 0 | 0 . 1 | 0 | 1 | 1 |
| G = |0 | 1 | 0 . 1 | 1 | 0 | 1| |
| 0 | 0 | 1 . 0 | 1 | 1 | 1 |
Формируем кодовые комбинации. Для этого сначала записываем все возможные информационные комбинации из трех символов (всего восемь комбинаций): 000, 001, 010, 011, 100, 101, 110, 111.
К информационным символам приписываем четыре проверочных символа, получающихся в результате умножения информационного вектора-строки (a1, a2, a3) на матрицу-дополнение P. Произведение есть вектор-строка (a4, a5, a6, a7):
(a1, a2, a3) * Р = (a4, a5, a6, a7).
Выразим проверочные символы через информационные при помощи операции сложения по модулю 2 (обозначается знаком ). Из вида матрицы G следует, что:
a4 = a1 a2
a5 = a2 a3
a6 = a1 a3
a7 = a1 a2 a3
| № | Комбинация символов на выходе | |||||||
| Комбинация на входе | | |||||||
| al | a2 | a3 | а4 | а5 | а6 | а7 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| 3 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | |
| 4 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | |
| 5 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | |
| 6 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 7 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |
Таблица2–разрешенныекомбинации
Алгоритмдекодирования. Составляем проверочную матрицу Н:
1 1 0 . 1 0 0 0
0 1 1 . 0 1 0 0
???? = | |
1 0 1 . 0 0 1 0
1 1 1 . 0 0 0 1
Вычисляем синдром (указателя позиции, в которой произошла ошибка) принятой кодовой комбинации. Синдром равен произведению принятого вектора-строки на транспонированную проверочную матрицу. Запишем выражение для синдрома через закодированный сигнал при помощи операции сложения по модулю 2:
С1=a1 a2 a4
С2=a2 a3 a5
С3=a1 a3 a6
С4=a1 a2a3a7
где a1, a2… a7 – принятый кодовый символ, возможно искаженный помехой.
Синдром не зависит от переданной комбинации. Он зависит только от позиции, в которой произошла ошибка.
Формируем вектор ошибки V, т.е. кодовую комбинацию, которая содержит единицу на той позиции, где произошла ошибка. Соответствие между значением синдрома и вектором ошибки устанавливает таблица 3.
| Вектор ошибки | 00000 00 | 00000 01 | 00000 10 | 00001 00 | 00010 00 | 00100 00 | 01000 00 | 10000 00 |
| Синдром | 0000 | 0001 | 0010 | 0100 | 1000 | 1101 | 0111 | 1011 |
Таблица3–Связьсиндромовивекторов ошибок
Рассмотрим пример коррекции одиночной ошибки.
Пусть передавали некоторую комбинацию
; приняли комбинацию (1101001) – это запрещенная комбинация (смотря в таблицу 1, очевидно, что ошибка в символе a3). Ее синдром: (С1С2С3С4) = 1111. Из таблицы 2 находим вектор ошибки (0010000), т.е. ошибка действительно произошла именно в третьем символе. Следовательно, исправив третий символ (0 на 1), получим правильную исходную передаваемую комбинацию: 1111001.
Изобразим структурные схемы кодера и декодера (рисунки 10 и 11):
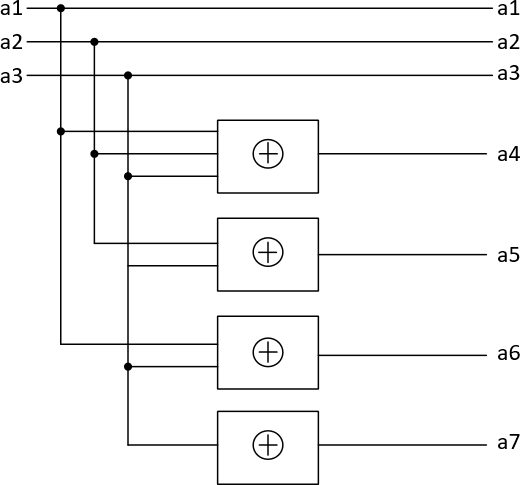
Рис.10–Структурнаясхемакодера
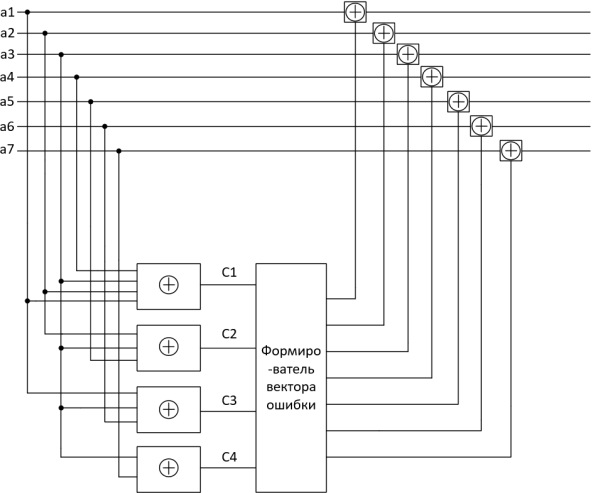
Рис.11–Структурнаясхемадекодера
-
Выберите короткую кодовую комбинацию: 01 или 10. Нарисуйте временную диаграмму двоичной комбинации. Изобразите временные диаграммы сигналов ДАМ, ДЧМ и ДФМ, соответствующие выбранной двоичной комбинации.
Выберем комбинацию 10 и построим для неё все требуемые диаграммы.
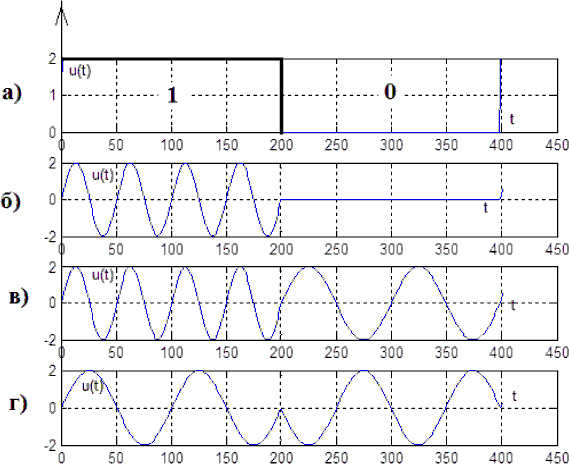
Рис.12-Временныедиаграммы:
а)двоичныйсигнал;б)сигналДАМ;в)сигналДЧМ;г)сигналДФМ.
-
Начертить структурные схемы модулятора и демодулятора для передачи и приема многопозиционных сигналов. Указать назначение блоков схемы. Зарисовать векторные диаграммы многопозиционных сигналов. Требуемые схемы представлены ниже:
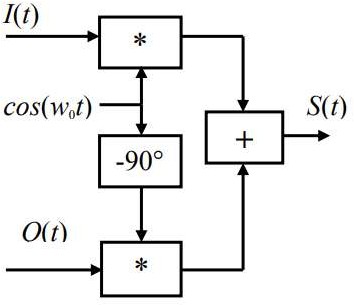
Рис.13-Структурнаясхема