Министерство образования и науки РФ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра экономики

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине «Финансовые вычисления»

Вариант № 2

студент гр. оз-Ф882П8-4

Коноплева Ксения Сергеевна

«27» апреля 2023 г.

ТОМСК 2023

Задание 1

Клиент поместил в банк 100 тыс. руб. под простую процентную ставку 11% годовых. Какая сумма будет на его счете через а) 7 месяцев; б) три года; в) 4 года 3 месяца? При расчете используйте формулу обычного процента с приближенным числом дней.

Решение

Формула расчета обычного процента:

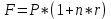(1.1)

P – первоначальная сумма

n - количество лет

r - процентная ставка

a) F = 100 ⋅ (1 + 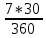⋅ 0,11) = 106,4 тыс. руб.

Через три года на счете накопится 106,4 тыс. рублей.

Величина начисленных за три года процентов составит:

106,4 − 100 = 6,4 тыс. руб.

б) F = 100 ⋅ (1 + 3 ⋅ 0,11) = 133 тыс. руб.

Через три года на счете накопится 133 тыс. рублей.

Величина начисленных за три года процентов составит:

133 − 100 = 33 тыс. руб.

в) n= 4 года 3 месяца= (360*4+3*30)/360=4,25

F = 100 ⋅ (1 + 4,25 ⋅ 0,11) = 146,7 тыс. руб.

Через четыре года три месяца на счете накопится 146,7 тыс. рублей.

Величина начисленных за четыре года три месяца процентов составит:

146,7 − 100 = 46,7 тыс. руб.

Задание 2

Предприниматель получил ссуду в 600 тыс. руб. на полгода. Банк предоставляет ссуду на условиях начисления простых учетных процентов по ставке 16% годовых. Какую сумму предприниматель будет должен банку?

Решение

Для определения наращения капитала по простой ставке ссудного процента, используем формулу:

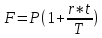(1.2)

По формуле (1.2) при P = 600 тыс. руб., n = 30*60=180 дней, r = 0,16, получаем:

F = 600 ⋅ (1 + 0,16 ⋅ 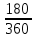) = 648 тыс. руб.

Предприниматель будет должен вернуть банку сумму 648 тыс.руб.

Задание 3

В банк вложены деньги в сумме 800 тыс. руб. на полтора года под 10% годовых с ежеквартальным начислением сложных процентов. Определите доход клиента в этой финансовой операции.

Решение

Размер возвращаемой суммы рассчитаем по формуле начисления сложных процентов:

---

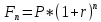(1.3)

Где n - количество лет

P= 800 тыс.руб.

n= 1,5 года

r=10%=0,1



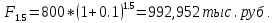
Тогда доход получим:

992,952 – 800 = 192,952 тыс. руб.

Задание 4

Определите дисконтированную сумму при учете 100 тыс. руб. по простой и сложной учетной ставкам, если годовая ставка равна 18% годовых и учет происходит за 30 дней, 180 дней, 1 год, 3 года, 5 лет. Полагать год равным 360 дней.

Решение

Для определения суммы, получаемой заемщиком, для простой учётной ставки формула:

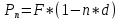(1.4)

Дисконт – доход, полученный по учетной ставке, т.е. разница между размером предоставляемого кредита и непосредственно выдаваемой суммой, считаем дисконт = F-P

F=100000 руб.

d=0,18

а) n=30 дней=0,083(3)

б) n=180 дней=0,5

в) n=1 год =1

г) n= 3 года =3

д) n= 5 лет =5

Применяем показатели у формуле (1.4):

а)

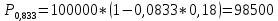
F – P = 100000 – 98500 = 1500

б)

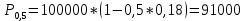
F – P = 100000 – 91000 = 9000

в)

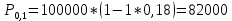
F – P = 100000 – 82000 = 18000

г)

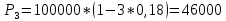
F – P = 100000 – 46000 = 54000

д)

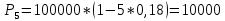
F – P = 100000 – 10000 = 90000

Для определения суммы, получаемой заемщиком, для сложной учётной ставки формула:

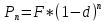(1.5)

По формуле (1.5) определяем суммы, получаемой заемщиком, для сложной учётной ставки:

а)

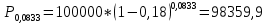
F – P = 100000 – 98359,9 = 1640,09

б)

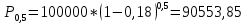
F – P = 100000 – 90553,85 = 9446,14

в)

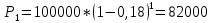
F – P = 100000 – 82000 = 18000

г)

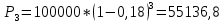
F – P = 100000 – 55136,8 = 44863,2

д)

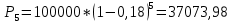
F – P = 100000 – 37073,98 = 62926,02

Получим таблицу сравнения дисконта:

Способ дисконтирования	30 дней	180 дней	1 год	3 года	5 лет
Простая ставка	1500	9000	18000	54000	90000
Сложная ставка	1640,09	9446,14	18000	44863,2	62926,02

---

Задание 5

Банк выдает ссуду под сложную процентную ставку 20% годовых. Какую простую годовую процентную ставку должен установить банк, чтобы его доход не изменился, если начисление процентов происходит а) по полугодиям; б) каждые 2 месяца; в) каждую неделю.

Решение

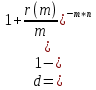(1.6)

По формуле (1.6) при: а) n = 0,5; б) n = 0,17; в) n = 0,02, r = 0,2 находим требуемую величину простой учётной ставки:

а)

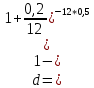
искомое значение простой учётной ставки составляет 22,41% годовых.

б)

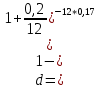
искомое значение простой учётной ставки составляет 23,29% годовых.

в)

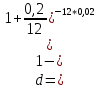
искомое значение простой учётной ставки составляет 23,71% годовых.

Задание 6

Контракт на выплату 10 000 долл. 1 ноября и выплату 5000 долл. 1 января следующего года необходимо заменить новым контрактом, в соответствии с которым 1 декабря выплачивается 6000 долл., оставшаяся сумма погашается 1 марта. Определить сумму второго платежа на основе простой ссудной ставки (следующий год не високосный).

Решение

Величину неизвестного платежа находим из условия эквивалентности контрактов. Приведенные стоимости платежей по старому контракту необходимо приравнять к приведенным стоимостям потоков платежей по новому контракту и из полученного уравнения определить неизвестную величину нового платежа:

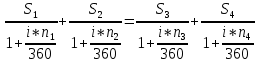(1.7)

Решение

S1 = 10000 долл. S2 = 5000 долл. S3 = 6000 долл.

Задание 7

Номинальная процентная ставка, компенсирующая при наращении инфляцию, составляет 48% годовых. Определите инфляцию за квартал, если начисление сложных процентов осуществляется каждый месяц.

Решение

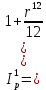(1.8)

Приравняем годовой индекс инфляции к множителю наращения за год. Полагаем r12 = 0,48, получим:



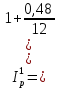
Поэтому индекс инфляции за квартал (0,25) составит:

---

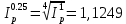
Следовательно, темп инфляции за квартал в среднем равен 12,49%.

Задание 8

В банк на депозит внесено 7000 долл., срок депозита — квартал, простая ссудная ставка равна 8% годовых. Ставка налога на начисленные проценты равна 2%. Определить наращенную сумму с учетом налога на проценты и реальную доходность финансовой операции.

Решение

Определим наращенную сумму с учетом налога на проценты:

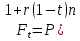(1.9)

где P – первоначальная сумма депозита;

r – ставка процента;

t – ставка налога;

n – число лет.

Используем формулу (1.9) при P = 7000; n = 0,25; t = 0,02; r = 0,08:



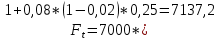
Наращенная сумма с учетом налога на проценты составит 7137,2 долларов.

Задание 9

Анализируются два плана накопления денежных средств по схеме аннуитета пренумерандо: 1) класть на депозит 200 тыс. руб. каждые полгода при условии, что банк начисляет сложные проценты по ставке 8% с ежеквартальным начислением процентов; 2) делать ежегодный вклад в размере 420 тыс. руб. при условии, что банк начисляет сложные проценты по ставке 7% с ежемесячным начислением процентов. Какая сумма будет на счете через 5 лет при реализации каждого плана?

Решение

Используем формулы оценки постоянного аннуитета:
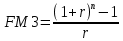(1.10)

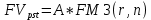(1.11)

План 1:

Принимая за базовый период полгода, воспользуемся формулами (1.10) и (1.11) при A = 200; r = 2%; n = 20:





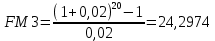
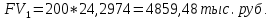
План 2:

Принимая за базовый период год, воспользуемся формулами (1.10) и (1.11) при A = 420; r = 0,00583%; n = 10:





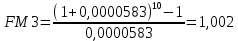
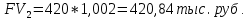
В данной задаче более предпочтительным является план 1, так как в этом случае будущая стоимость денежного потока выше.

Задание 10

Банк предлагает ренту постнумерандо на 15 лет с полугодовой выплатой 100 тыс. руб. Годовая процентная ставка 9% в течение всего периода остается постоянной, сложные проценты начисляются по полугодиям. По какой цене имеет смысл приобретать эту ренту?

---

Решение

Приведенная стоимость ренты постнумерандо равна:

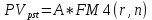(1.12)

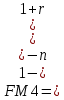(1.13)
Используем формулы (1.12) и (1.13), считая полугодие базовым периодом:





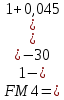
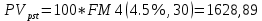
Ренту можно приобрести за 1 628 890 руб.

---

Смотрите также файлы

• 8 сентября 1802 года Александром Павловичем был подписан Манифест о создании министерств, что стало заметным шагом в направлении улучшения государственной структуры управления.docx

• План урока физкультуры 3 3 класс Раздел.docx

• Доклад по биологии на тему Луи Пастер выполнил Мальцев Андрей кадет 9 а класса Истомино 2022 Введение.docx

• Тема Определение, структура и виды общения Задание 1.docx

• У меня есть для вас видеоблог. У нас сейчас обеденный перерыв. У меня сейчас фотосессия. Фотограф и его ассистенты едят на заднем дворе. Но мне нельзя сейчас есть, потому что я хочу продолжить фотосессию после перерыва.docx