Добавлен: 07.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Отчет по лабораторной работе №13
По дисциплине ФИЗИКА
(наименование учебной дисциплины согласно учебному плану)
Тема: Измерение параметров емкостей в цепи переменного тока
Автор: студент гр. ПМК-22 Николаев А. А.
(шифр группы) (подпись) (Ф.И.О.)
ОЦЕНКА:
Дата:
ПРОВЕРИЛ
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2023 год
Цель работы: Определение импеданса, сдвига фаз и измерение ёмкости на разных частотах в резистивно-ёмкостной цепи.
Краткое теоретическое содержание
Изучаемое явление - явление импеданса.
Определения основных физических понятий, объектов, процессов и величин
Переменный ток – это электрический ток, изменяющийся по времени.
Реактивный элемент – устройство, способное накопить электрическую энергию, подведенную к нему в виде напряжения или тока от генератора, и затем отдать её в нагрузку.
Индуктивность – коэффициент пропорциональности между магнитным потоком и величиной этого тока.
Виды сопротивлений: ёмкостное (создаваемое конденсатором), индуктивное (создаваемое катушкой), активное (электрической цепи или её участка), реактивное (элемента схемы, вызванное изменением тока или напряжения из-за индуктивности или ёмкости того элемента) и импеданс.
Ёмкостное сопротивление – величина,
характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка).
Импеданс – комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала, аналог электрического сопротивления для гармоничных процессов.
Электрическая ёмкость – характеристика проводника, мера его способности накапливать электрический заряд.
Фазовый сдвиг – разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
Закон Ома – физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника.
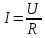 ,
,где I – сила тока (А), U – напряжение (В), R – сопротивление (Ом).
Связь циклической частоты и частоты сигнала:
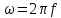
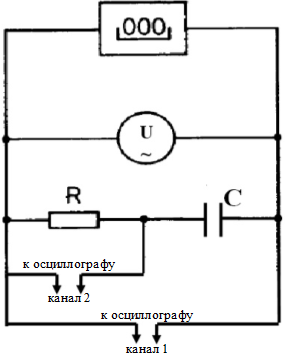
Схема установки

Схема представлена в виде последовательно соединённых резистора R и конденсатора C, замкнутых на источнике переменного тока U. А с учётом подключённых к этой схеме измерительных приборов окончательный вид схемы, где выходы 1 и 2 идут соответственно с резистора и блока питания на осциллограф. К источнику тока (функциональному генератору) параллельно подключён цифровой счётчик.
Основные расчётные формулы
-
Циклическая частота:
-
Емкостное сопротивление:
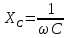
-
Ёмкость конденсатора:
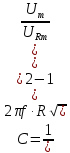
где f – частота (Гц), R – сопротивление резистора (Ом), Um – амплитудное напряжение (В), URm – амплитудное напряжение на резисторе (В).
-
Импеданс (полное сопротивление):
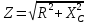
где R – сопротивление резистора (Ом), XC – реактивное сопротивление конденсатора (Ом).
-
Амплитудно-частотная характеристика (действующее значение силы тока в цепи):
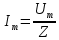
где Um – амплитудное напряжение (В), Z – импеданс цепи (Ом).
-
Теоретический фазовый сдвиг:
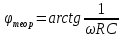
где - циклическая частота (Гц), R – сопротивление цепи (Ом), C – емкость конденсатора (Ф).
-
Измеренный фазовый сдвиг:
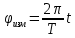
где T – период (с), t – время (с).
где - циклическая частота (Гц), C – измеренная емкость конденсатора (Ф).
где f – частота сигнала (Гц).
Формулы для расчёта погрешностей косвенных измерений
Абсолютная погрешность измерений емкости конденсатора:
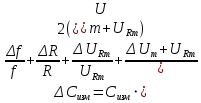
Абсолютная погрешность измерений фазового сдвига
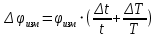
Абсолютная погрешность измерений циклической частоты:
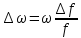
Абсолютная погрешность измерений емкостного сопротивления:
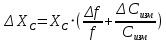
Абсолютная погрешность измерений силы тока:
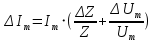
Абсолютная погрешность измерений импеданса:
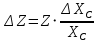
Погрешности прямых измерений
∆t=∆T=0,1 мс
∆Um=∆URm=0,2 В
∆f=1 Гц
Исходные данные:
R=200 Ом,
C=1 мкФ
Обработка результатов
Таблица 1 - Измерение напряжений и емкостей в RC-цепи
| f, кГц | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 |
| Um, В | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 |
| URm, В | 0,50 | 1,00 | 1,40 | 1,70 | 2,00 | 2,10 | 2,60 | 2,80 | 3,00 | 3,10 |
| Cизм, мкФ | 1,00 | 1,03 | 0,99 | 0,93 | 0,92 | 0,82 | 0,97 | 0,98 | 1,00 | 0,98 |
| Z, Ом | 1604,07 | 820,52 | 566,96 | 445,32 | 375,93 | 332,21 | 302,81 | 282,10 | 266,97 | 255,60 |
Пример вычисления для опыта 1:
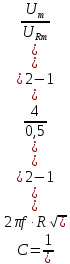
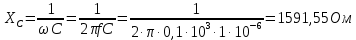
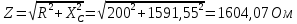
Таблица 2 - Измерение фазового сдвига в RC-цепи
| f, кГц | 0,05 | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 |
| t, с | 5,00 | 2,20 | 0,70 | 0,40 | 0,20 | 0,10 | 0,08 | 0,04 | 0,03 | 0,02 | 0,01 |
| T, с | 19,00 | 10,00 | 5,00 | 3,30 | 2,50 | 2,00 | 1,70 | 1,40 | 1,20 | 1,10 | 1,00 |
| φизм, рад | 1,65 | 1,38 | 0,88 | 0,76 | 0,50 | 0,31 | 0,30 | 0,18 | 0,16 | 0,11 | 0,06 |
| φтеор, рад | 1,51 | 1,45 | 1,32 | 1,21 | 1,11 | 1,01 | 0,92 | 0,85 | 0,78 | 0,72 | 0,67 |
Пример вычисления для опыта 1:
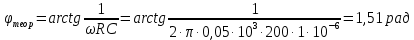
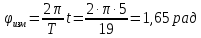
Вычисление косвенных погрешностей:
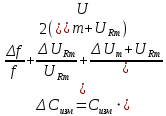
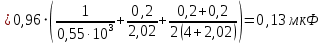
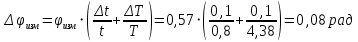
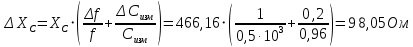
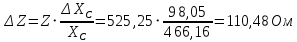
Графический материал
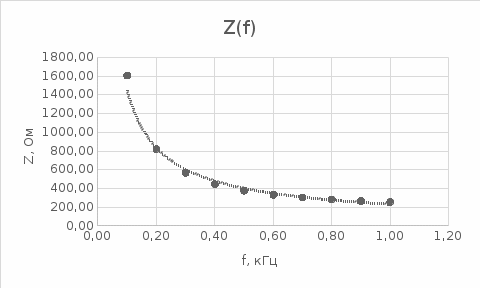
Рис. 1 - Зависимость импеданса от частоты сигнала
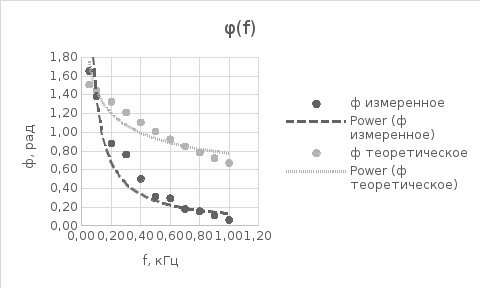
Рис.2 Зависимость сдвига фаз от частоты
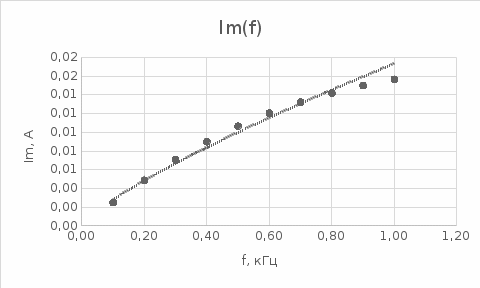
Рис. 2 - Зависимость силы тока от частоты сигнала
Конечные результаты
Емкость конденсатора с учётом абсолютной погрешности
C=0,96±0,13 мкФ
Вывод
Вычисленное среднее значение емкости конденсатора С=0,96мкФ отличается от заданной емкости в 1 мкФ на 4%
Построенные графики зависимостей полного сопротивления цепи, фазового сдвига, силы тока в цепи от частоты отражающие следующие зависимости:
-
при увеличении частоты импеданс уменьшается; -
при увеличении частоты фазовый сдвиг уменьшается -
при увеличении частоты сила тока возрастает.