Лекция 12

Интегрирование уравнений Лапласа в цилиндрических координатах
Ключевые слова: уравнение Лапласа,цилиндрические координаты,метод разделения переменных,уравнение Бесселя,цилиндрические функции, функция Бесселя, функция Неймана.
Уравнение Лапласа в цилиндрических координатах имеет следующий вид:

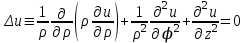. (4.1)

Решение этого уравнения ищем методом Фурье. Положим, что

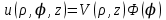(4.2)

и подставим это произведение в уравнение (4.1). Тогда получим два уравнения

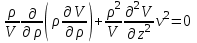, (4.3)

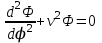. (4.4)

К первому уравнению еще раз применим метод Фурье. Пусть

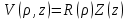. (4.5)

Для функций 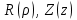получим следующие обыкновенные дифференциальные уравнения

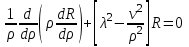, (4.6)

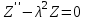. (4.7)

Общие решения уравнений (4.4) и (4.7) имеют вид:

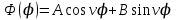, (4.8)

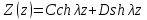. (4.9)

Уравнение (4.6) можно представить в виде



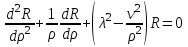
Это уравнение называется уравнением Бесселя. Интегралы этого уравнения называются цилиндрическими функциями или функциями Бесселя:

,

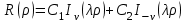где 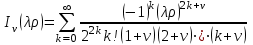- бесселева функция первого рода порядка .

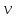Если 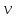есть целое число (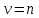

---

), то решение уравнения Бесселя выражается формулой

,

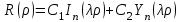где 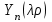- функция Бесселя второго рода, которую еще называют функцией Неймана.

---

Смотрите также файлы

• T meBeauty of the soul.pdf

• Расчёт параметров посадки.docx

• Наземные съеМКи местности общие сведения о съемке местности Топографической съемкой.doc

• Ядерная медицина.pdf

• Что такое онтогенез и филогенез Какова их взаимосвязь Сущность онтогенеза.odt