«Формирование универсальных учебных действий на уроках математики в 5 классе»

Деятельность формируется в деятельности.

Л.С. Выготский.

Современное информационное общество запрашивает человека обучаемого, способного самостоятельно учиться и многократно переучиваться в течение жизни, готового к самостоятельным действиям и принятию решений. Для жизни человека важно не наличие у него накопленного впрок, запаса какого-то внутреннего багажа всего усвоенного, а проявление и возможность использовать его функциональные, деятельностные качества. Вот почему в настоящее время проблема самостоятельного успешного усвоения обучающимися новых знаний, умений и компетенций, включая умение учиться, приоритетна.

Большие возможности для этого представляет освоение универсальных учебных действий. Именно поэтому «Планируемые результаты» Федерального государственного образовательного стандарта (ФГОС) определяют не только предметные, но и метапредметные (умственные действия учащихся, направленные на анализ и управление своей познавательной деятельностью), а также личностные результаты.

Разработка концепции развития универсальных учебных действий в системе российского образования отвечает новым социальным запросам,

отражающим переход к информационному обществу, основанному на знаниях и высоком инновационном потенциале.

Целью образования становится общекультурное, личностное и познавательное развитие обучающихся, обеспечивающее такую ключевую компетенцию, как умение учиться.

Безусловно, в формировании учебных универсальных действий (УУД) ведущую роль играет учитель. Учитель призван осуществлять скрытое управление процессом обучения, быть вдохновителем обучающихся.

Ученик из присутствующего и пассивно исполняющего указания учителя на уроке традиционного типа теперь становится главным деятелем.    А современному учителю необходимо искать новые подходы к организации учебного процесса, нацеленного на формирование УУД, используя различные методики и технологии обучения.

---

Логика развития универсальных учебных действий строится по формуле: от действия к мысли.Развитие личности в системе образования обеспечивается через формирование универсальных учебных действий. Овладение обучающимися универсальными учебными действиями создает возможность самостоятельного успешного усвоения новых знаний, умений и компетентностей, включая организацию усвоения, т.е. умения учиться.

Для успешного освоения обучающимися образовательных программ необходимо сформировать у учащихся следующие виды УУД:

1. 
   Личностные. Система ценностных ориентаций школьника, отражающих личностные смыслы, мотивы, отношения к различным сферам окружающего мира. Личностные УУД выражаются формулами «Я и природа», «Я и другие люди», «Я и общество», «Я и познание», «Я и я».
   

В математике: смыслообразование.

2. 
   Регулятивные. Отражают способность обучающегося строить учебно-познавательную деятельность, учитывая все ее компоненты (цель, мотив, прогноз, средства, контроль, оценка).
   

В математике: целеполагание, планирование, прогнозирование, контроль, оценка, алгоритмизация действий.

3. 
   Познавательные. Система способов познания окружающего мира, построение самостоятельного процесса поиска, исследования и совокупность операций по обработке, систематизации, обобщению и использованию полученной информации.
   

В математике:

общеучебные – моделирование, выбор наиболее эффективного способа решения задач;

познавательно-логические – анализ, синтез, сравнение, группировка, причинно-следственные связи, логические рассуждения, доказательства, практические действия.

4. 
   Коммуникативные. Способность обучающегося осуществлять коммуникативную деятельность, использования правил общения в конкретных учебных и внеурочных ситуациях; самостоятельная организация речевой деятельности в устной и письменной форме.
   

В математике: использование средств языка и речи для получения информации, участия в продуктивном диалоге, самовыражение, монологические высказывания разного типа.

Для формирования универсальных учебных действий на уроках математики можно выделить 4 этапа:

• 1 этап — вводно-мотивационный.

Чтобы ученик начал «действовать», необходимы определенные мотивы. На уроках математики необходимо создать проблемные ситуации

---

, где ученик проявляет умение комбинировать элементы для решения проблемы. На этом этапе ученики должны осознать, почему и для чего им нужно изучать данную тему, и изучить, какова основная учебная задача предстоящей работы. (Используется технология проблемного обучения.)

• 2 этап — открытие математических знаний.

На данном этапе решающее значение имеют приемы, требующие самостоятельных исследований, стимулирующие рост познавательной потребности.

• 3 этап — формализация знаний.

Основное назначение приемов на этом этапе - организация деятельности обучающихся, направленная на всестороннее изучение установленного математического факта.

• 4 этап — обобщение и систематизация.

На этом этапе применяют приемы, которые устанавливают связь между изученными математическими фактами, приводят знания в систему.

Формирование и развитие УУД на уроках математики происходит с помощью различных видов заданий.

Виды заданий для формирования УУД:

личностные:

• 
  Участие в проектах
  
• 
  Подведение итогов урока
  
• 
  Творческие задания
  
• 
  Мысленное воспроизведение ситуации
  
• 
  Самооценка событий
  
• 
  Дневники достижений
  

регулятивные:

• 
  Преднамеренные ошибки
  
• 
  Поиск информации в предложенных источниках
  
• 
  Взаимоконтроль
  
• 
  «Найди ошибку»
  

познавательные:

• 
  Упорядочивание
  
• 
  «Цепочки»
  
• 
  Составление схем-опор
  
• 
  Работа с разного вида таблицами
  
• 
  Составление и распознавание диаграмм
  
• 
  Поиск лишнего
  

коммуникативные:

• 
  Составь задание однокласснику
  
• 
  Оцени работу товарища
  
• 
  Работа в группах
  
• 
  «расскажи …», «объясни…», «прокомментируй…» и другое
  

Именно математика в ряду других учебных дисциплин занимает одну из лидирующих позиций в формировании учебно-познавательной компетенции обучающихся. Поскольку в первую очередь, при обучении математике у учащихся развиваются такие свойства интеллекта, как:

• 
  математическая интуиция (на методы решения задач, на образы, свойства, способы доказательства, построения);
  
• 
  логическое мышление (понятия и общепонятийные связи, владение правилами логического вывода, понимание и сохранение в памяти важных доказательств);
  
• 
  понимание логического строения математической теории (на примере ознакомления в общих чертах с аксиоматическим строением евклидовой геометрии);
  
• 
  пространственное мышление (пространственные абстракции, анализ и синтез геометрических образов, пространственное воображение);
  
• 
  техническое мышление, способность к конструктивно-математической деятельности(понимание сущности скалярных величин, умение определять, измерять и вычислять длины, площади, объемы геометрических фигур, умение изображать геометрические фигуры и выполнять геометрические построения, моделировать и конструировать геометрические объекты);
  
• 
  комбинаторный стиль мышления (поиск решения проводится на основе целенаправленного перебора возможностей, круг которых ограничен определенным образом);
  
• 
  алгоритмическое мышления, необходимое для профессиональной деятельности в современном обществе;
  
• 
  владение символическим языком математики (понимание математических символов, умение записывать в символической форме решения и доказательства);
  
• 
  математические способности школьников (способности к абстрагированию и оперированию формальными структурами, обобщению).
  

---

• 
  Результаты формирования универсальных учебных действий
  
• 
  Результатом формирования личностных УУД следует считать:
  
  • 
    уровень развития морального сознания;
    
  • 
    присвоение моральных норм, выступающим регулятором морального поведения;
    
  • 
    полноту ориентации учащихся на моральное содержание ситуации.
    
• 
  Критериями сформированности у учащегося регулятивных УУД может стать способность:
  
  • 
    выбирать средства для своего поведения;
    
  • 
    планировать, контролировать и выполнять действие по заданному образцу, правилу, с использованием норм;
    
  • 
    планировать результаты своей деятельности и предвосхищать свои ошибки;
    
  • 
    начинать и заканчивать свои действия в нужный момент.
    
• 
  Результатом формирования познавательных УУД будут являться умения:
  
  • 
    выделять тип задач и способы их решения;
    
  • 
    осуществлять поиск необходимой информации, которая нужна для решения задач;
    
  • 
    различать обоснованные и необоснованные суждения;
    
  • 
    обосновывать этапы решения учебной задачи;
    
  • 
    производить анализ и преобразование информации;
    
  • 
    проводить основные мыслительные операции (анализ, синтез, классификации, сравнение, аналогия и т.д.);
    
  • 
    устанавливать причинно-следственные связи;
    
  • 
    владеть общим приемом решения задач;
    
  • 
    создавать и преобразовывать схемы необходимые для решения задач;
    
  • 
    осуществлять выбор наиболее эффективного способа решения задачи исходя из конкретных условий.
    
• 
  Основным критерием сформированности коммуникативных действий можно считать коммуникативные способности ребенка, включающие в себя:
  
  • 
    желание вступать в контакт с окружающими (мотивация общения «Я хочу!»);
    
  • 
    знание норм и правил, которым необходимо следовать при общении с окружающими;
    
  • 
    умение организовывать общение, включающее умение слушать собеседника, умение решать конфликтные ситуации.
    

Примеры заданий для формирования УУД на уроках математики в 5 классе

Задания	Содержание учебной деятельности
Познавательные УУД
1. В велогонке Дима, Саша, Андрей и Вася заняли со второго по пятое места. Саша обогнал Диму на 39с., но отстал от Васи на 41с. Андрей был впереди Васи на 12., но отстал от победителя на 13с. В каком порядке финишировали мальчики, и с каким отставанием от победителя? Д С В А 39с. 41с. 12с. 13с. В задаче сказано, что «Саша обогнал Диму», значит, Дима отстал на 39 с. и т.д. по рисунку видно, что первым финишировал Андрей, за ним Вася, Саша и Дима. Андрей отстал от победителя на 13(с.); Вася на 13+12=25 (с.); Саша на 25+41=66(с.)=1мин.6с.; Дима на 66+39=105 (с.)=1мин 45с.	Установление причинно-следственных связей; построение логической цепи рассуждений; моделирование.
2. Найдите выражения, значения которых равны: (128+57)∙36; 43∙25+62∙25; (1355-955)∙68; (43+62)∙25; 1355∙68-955∙68; 128∙36+57∙36. Объясните, как их искали: а) Назовите математическое свойство, на основании которого равны эти выражения; б) запишите это свойство в виде равенства; в) сравните свою запись с такой: (a+b)∙c = a∙c+b∙c. Сделайте вывод.	Происходит поиск и выделение необходимой информации; анализ с целью выделения общих признаков; синтез, как составление целого из частей; знаково-символическое моделирование.
3. С двух яблонь собрали 67 кг. яблок, причем с одной яблони собрали на 19 кг. больше, чем с другой. Сколько килограммов яблок собрали с каждой яблони? Масса яблок 1-я яблоня 67 кг. 2-я яблоня	Поиск и выделение информации; выбор критериев для сравнения; знаково-символическое моделирование.
	Общеучебные действия: поиск и выделение информации; формирование умения выделять закономерность. Логические действия: построение логической цепи рассуждений.
5.Цена одного волейбольного мяча х р., а баскетбольного мяча у р. Что обозначают выражения: 3х, 4у, 5х+2у, 15х-2у, 4(х+у)?	Знаково-символическое моделирование. Постепенно обучающиеся учатся соотносить буквенные выражения с реальной ситуацией, описываемой в задаче.
6. Привезли 12 кг яблок, по 30кг в каждом, и 8 ящиков груш, по 40 кг в в каждом. Какой смысл имеют следующие выражения а) 30∙12 в) 40∙8 д) 30∙12+40∙8 б) 12-8 г) 40-30 е)30∙8-40∙8?	Поиск и выделение необходимой информации; анализ с целью выделения общих признаков; синтез, как составление целого из частей; моделирование.
7. Дополните каждый треугольник, изображенный на рисунке , до прямоугольника и найдите площадьи треугольников. 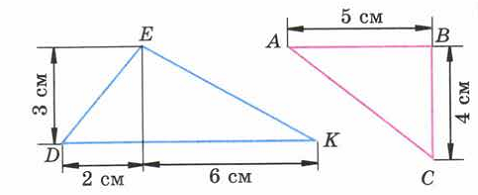8. Постройте фигуру, равную фигуре, изображенной на рисунке	Решение данных задач является подготовкой к изучению геометрии. Они формируют у учащихся понятие плоской фигуры, а так же умение строить эти фигуры и использовать их свойства при ре-шении задач. Общеучебные: - умение самостоятельно применять свои знания на практике; - поиск и выделе-ние необходимой информации; - моделирование. Логические: - анализ с целью выделения признаков (существенных, несущественных); - синтез как составление целого, восполняя недостающие компоненты. Действия постановки и решения проблем: - самостоятельное создание способов решения проблем творческого и поискового характера.
Регулятивные
9. Запишите цифрами числа, встречающиеся в тексте: «Миллиард – очень большле число. За тридцать лет с первого января тысяча девятьсотсемидесятого года по тридцать первое декабря тысяча девятьсот девяносто девятого года прошло днсять тысяч девятьсот пятьдесят семь суток, что составляет двести шестьдесят две тысячи девятьсот шестьдесят восемь часов, или девятьсот сорок шести миллионов шестьсот восемьдесят четыре тысячи восемьсот секунд. Значит, за тридцать лет не проходит и миллиарда секунд».	Анализ текста, нахождение в тексте нужной информации. Анализ собственной работы.
10. Верно ли, что: а) 341+569=910; г) 98∙57=23 790:78 б) 25∙42=10 500 д) 23∙27<630 в) 192:32=38-32 е) 1 288:56>40	Контроль в форме сравнения способа действия и его результата с целью обнаружения ошибок , и внесения необходимых корректив.
11. Согласны ли вы с утверждением: а) равные фигуры имеют равные площади; б) неравные фигуры имеют различные площади; в) любой квадрат есть прямоугольник; г) некоторые прямоугольники являются квадратами; д) если периметры прямоугольников равны, то равны и эти прямоугольники?	Контроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив.
12. На вершину холма ведут пять тропинок. Сколько существует способов подняться на холм и спустится с него, если подниматься и спускаться по разным тропинкам?	Составление плана и последовательности действий; способность к волевому усилию в преодолении препятствий.
13. Саша любит решать трудные задачи. Он рассказал, что за четыре дня смог решить 23 задачи. В каждый следующий день он решал больше задач, чем в предыдущий, и в четвертый деньрешил вчетверо больше, чем в первый. Сколько задач решил Саша в каждый из этих четырех дней?	Определение последовательности промежуточных целей с учетом конечного результата, составление плана и последовательности действий
14.Подумайте, по какому правилу составлен ряд чисел, и найдите три следующих числа: а) 20,22,24,… г) 1,4,9,16,… б) 2,4,8,16,… д) 2,5,4,8,6,11,… в) 1,3,9,… е) 1,8,27,…	Формирование целевых установок учебной деятельности, выстраивание последовательности, необходимых операций (алгоритм действий)
15. Подумайте,какие из чисел могут быть точными, какие приближенными: а) в классе 32 ученика; б) расстояние от Москвы до Киева 900км; в) у параллелепипеда 12 ребер; г) длина стола 1,3 м; д) население Москвы 8 млн человек; в) пакете0,5 кг муки; ж) площадь острова Куба 105 000 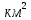; з) в школьной библиотеке 10 000 книг; и) одна пядь равна 4 вершкам, а вершок равен4,45см (вершок – длина фаланги указательного пальца).	Контроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив.

---

Личностные УУД

---

Смотрите также файлы

• Руководство для учителей 1 класса общеобразовательной школы Рекомендовано Министерством образования и науки.docx

• Календарнотематический план По предмету "Алгебра и начала анализа","Алгебра жне анализ бастамалары".docx

• Картотека подвижных игр с мячом в детском саду подвижная игра мяч в кругу для детей 34 года Цель.docx

• выбор поставщика.doc

• Протокол заседания цк рсдрп(б) от 21 октября (3 ноября) 1917 г.odt