Министерство образования Российской Федерации

Красноярский государственный университет

Кафедра общей физики

ОБЩАЯ ФИЗИКА

МОЛЕКУЛЯРНАЯ ФИЗИКА

План-конспект семинарских занятий

Часть 1

Красноярск 2006

Молекулярная физика преподается студентам физических специальностей как курс современной физики, демонстрирующий возможности таких универсальных методов, как термодинамический и статистический. Эти методы находят широкое применение не только в различных областях физики, но также в химии, биологии, биофизике, медицине, экономике и сфере гуманитарных наук. Раскрытие сущности статистического подхода на материале собственно молекулярной физики и примерах-аналогах из других областей реальной жизни является одной из главных задач семинарских занятий первой половины семестра.

Молекулярная статистика требует определенной математической подготовки студентов. Если в области дифференциального и интегрального исчисления стартовые знания, умения и навыки обнадеживают, то в области теории вероятностей они полностью отсутствуют. Поэтому основные понятия, аксиомы и правила теории вероятностей включены в «План-конспект»а кроме того в тексте приведены ссылки на дополнительные источники информации.

Многие задачи молекулярной физики имеют формализованные решения. Способ решения – действие по процедуре. Знание процедуры и умение ее выполнять позволяют с вероятностью, близкой к единице, решить задачу. И наоборот, незнание делает задачу для студента неразрешимой. План-конспект по каждой из восьми тем раздела «Статистический подход к описанию молекулярных явлений» содержит установочную теоретическую часть (физические идеи, проблематика, список определений и процедур), методические указания и набор задач.

Целевое назначение данного методического пособия – обеспечить максимальную согласованность содержания лекционного курса и семинарских занятий.

3

Список литературы

1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высш. шк., 2000.

2. Иродов И.Е. Задачи по общей физике. – М.: Бином, 1998.

3. Матвеев А.Н. Молекулярная физика. – М.: Высш. шк., 1987.

4. Москвич О.И., Бомбенко О.Н. Общая физика. Молекулярная физика: Структурированный конспект лекций. Ч.1. – Красноярск, РИС КрасГУ, 2006.

5. Рейф Ф. Статистическая физика. Берклеевский курс физики. Т.5. – М.: Наука, 1986.

6. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. /Под ред. Д.В.Сивухина. – М.: Наука, 1976.

7. Сивухин Д.В. Общий курс физики. Т.2. – М.: Наука, 1979.

40

Основные формулы элементарной комбинаторики

Число способов размещения m различных предметов по n местам:

(1.3)

Число способов размещения n различных предметов по n местам (число перестановок):

Г₂=n! (1.4)

Число способов размещения m неразличимых предметов по n местам:

---

. (1.5)

Число способов, которыми можно выбрать m различных предметов из n различных предметов, называется числом сочетаний и определяется выражением

(1.6)

Непрерывное распределение вероятности. Плотность вероятности. Условие нормировки вероятности

Если состояние физической системы характеризуется параметром , случайно принимающим любые значения от ₀ до ₁, то определение вероятности (1.1) лишено смысла, поскольку множество значений параметра не является счетным. В этом случае вероятность определяется в дифференциальной форме:

(1.7)

Утверждается, что dP() пропорциональна величине достаточно малого интервала изменений переменной d, а коэффициент пропорциональности f() не зависит от величины этого интервала и называется плотностью вероятности [1,5]:

5

диаметр молекулы CO₂. Атмосферное давление P₂ = 735 мм. рт. ст. Процесс считать изотермическим при температуре 15C.

О т в е т ы

9.1. , .

9.2. .

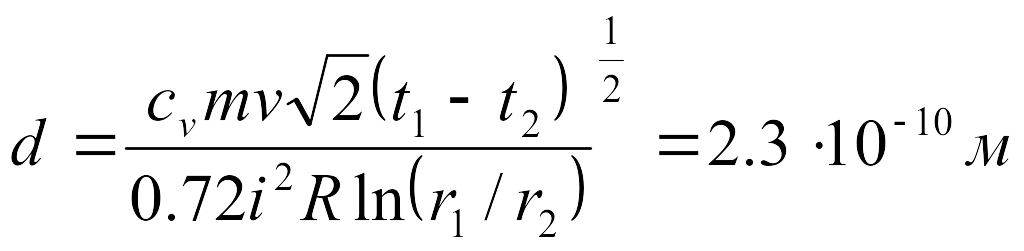9.3.

для плоскопараллельного слоя =

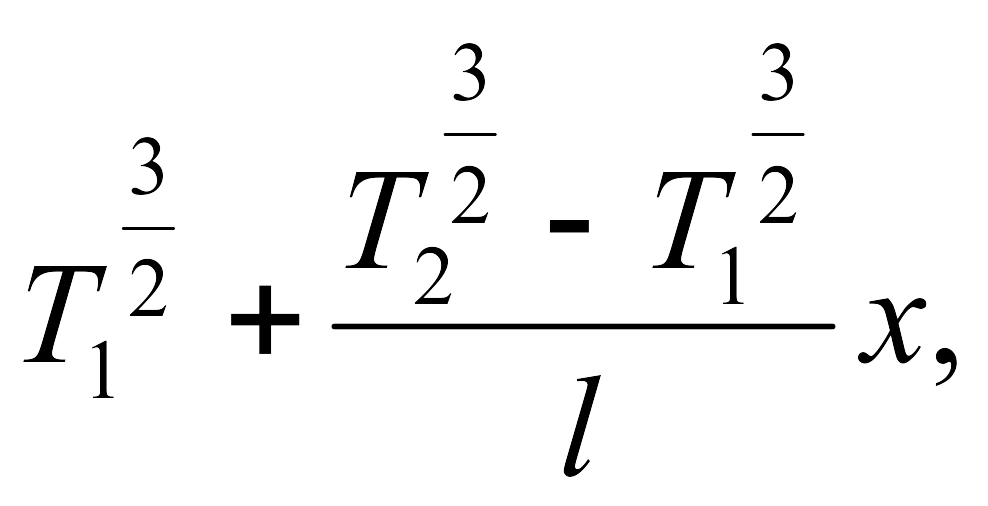
для сферического слоя ,

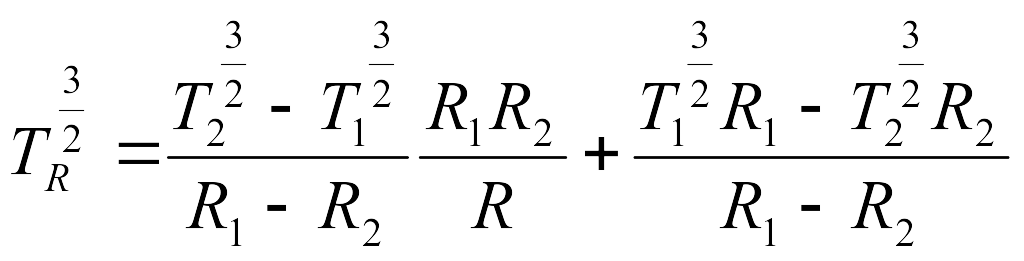для цилиндрического слоя .

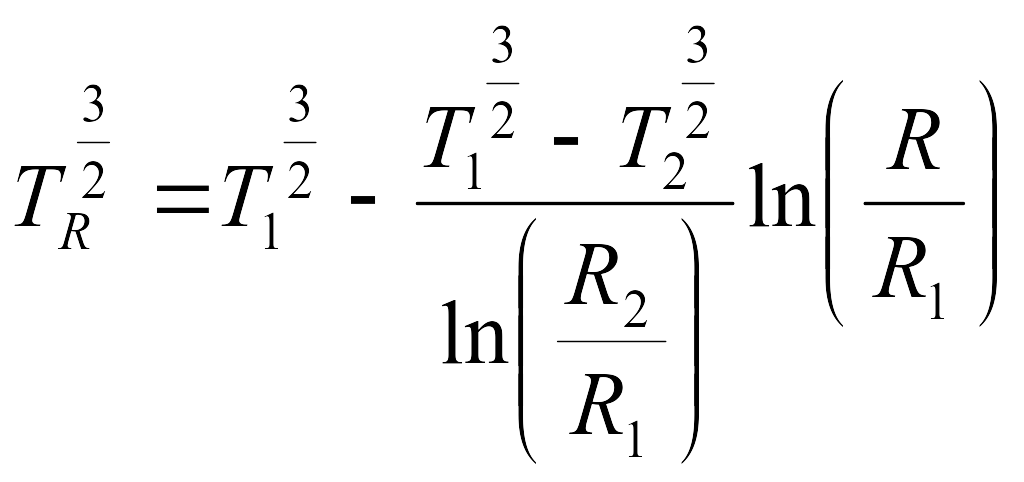9.4. .

9.5. .

9.6. .

9.7. .

38

Условие нормировки есть математическая запись утверждения, что если физическая система существует, то она находится в каком-либо из доступных ей состояний, характеризующихся параметром . Это событие является достоверным и его вероятность равна единице.

З а д а ч и

1.1. В сосуде находятся 5 молекул газа. Мысленно разобьем сосуд на две равные части. Каждая из молекул может находиться в выделенной половине объема или не находиться в ней. Рассмотреть "макроскопическое" состояние, когда m молекул газа находятся в выделенной половине сосуда, и найти число микроскопических состояний Г_m, с помощью которых оно реализуется. Принять m равным 0, 1, 2, 3, 4, 5. Определить также общее число микросостояний Г₀ и частоту реализации всех рассмотренных «макросостояний». Термин «макроскопическое состояние» здесь использован условно, поскольку в системе всего 5 частиц, и она, строго говоря, не является статистической. По этой же причине вместо «вероятность» употребляется термин «частота».

1.2. В системе из n частиц со спином 1/2 в отсутствии внешнего магнитного поля спин каждой частицы может быть равновероятно ориентирован либо вверх, либо вниз.

а) Найти вероятность P_n(m) реализации состояния, когда m спинов направлены вверх.

б) Построить гистограмму зависимости P(m) для n=6. Как будет изменяться вид распределения P(m) при увеличении чисел n и m? Чему равно наивероятнейшее значение m?

1.3. Состояние системы характеризуется случайной величиной x с известным распределением вероятности:

а) б)

в) г)

7

, (9.5)

где Q – масса ежесекундно протекающего через сечение трубы газа, r – радиус трубы,  - плотность газа,  - вязкость, P – давление газа;

б) кнудсеновское течение (для ультраразреженного газа, >> 2r, через капилляры) описывается уравнением

, (9.6)

где N – поток молекул через сечение трубки S, n – концентрация разреженного газа.

---

З а д а ч и

9.1. На основе обобщённого уравнения переноса получить зависимость коэффициентов переноса (D,,) от микроскопических и макроскопических параметров системы.

9.2. Для измерения теплопроводности азота им наполнили пространство между двумя длинными коаксиальными цилиндрами, радиусы которых r₁ = 0,5 см и r₂ = 2 см. Внутренний цилиндр равномерно нагревается спиралью, по которой проходит ток силой i = 0,1 А. Сопротивление спирали, приходящееся на единицу длины цилиндра, равно R = 0,1 Ом. Внешний цилиндр поддерживается при температуре t₂ = 0C. При установившемся процессе оказалось, что температура первого цилиндра t₁ = 93C. Найти газокинетический диаметр молекулы азота. Давление газа таково, что конвекцией можно пренебречь.

9.3. Пользуясь полученной в задаче 9.1. зависимостью (T), найти стационарное распределение температуры в плоско-параллельном слое газа толщины l, на границах которого поддерживаются постоянные температуры T₁ и T₂. Нагревание производят таким образом, что конвекции не возникает. Найти также стационарное распределение температуры для сферичес-

36

б)

С ростом числа частиц в системе n гистограмма переходит в график непрерывного распределения вероятности. Кривая представляет собой очень высокий и узкий пик, максимум которого находится при m_н=n/2.

1.3. а) б) А=2; в) г)

1.5. Площади под кривыми f(x) во всех случаях одинаковы и равны единице. Это условие нормировки плотности вероятности.

Семинар 2. Средние значения физических величин

и их флуктуации [1,4]

Среднее значение непрерывно изменяющейся случайной величины  определяют по формуле

(2.1)

здесь  может принимать значения в интервале (+ (смотри примечание к формуле (1.8)).

Среднее значение дискретно изменяющейся случайной величины

(2.2)

9

молекул газа, можно регистрировать на шкале. Положению покоя соответствует угол поворота =0. а) Как изменится средний квадрат угловой скорости , если момент инерции зеркальца увеличить в раз, температуру воздуха в комнате уменьшить в раз. б) Как изменится средний квадрат углового отклонения , если длину и диаметр нити увеличить соответственно в и раз, а температуру воздуха уменьшить в раз.

О т в е т ы

8.1. К=5/2PV= .

8.2. а) ,б) .

8.3. , .

8.4.

8.5. NaCl: , .

6. .

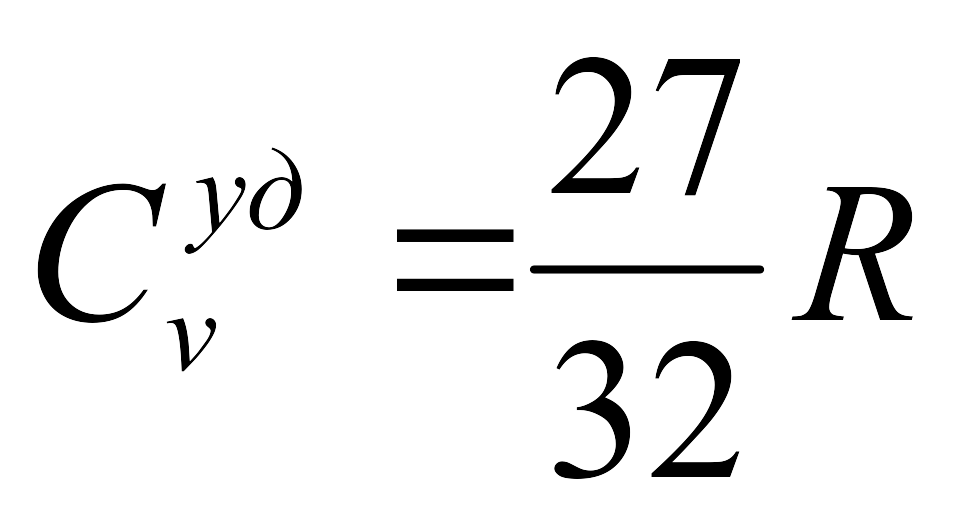7. а) Уменьшится в ². б) Увеличится в 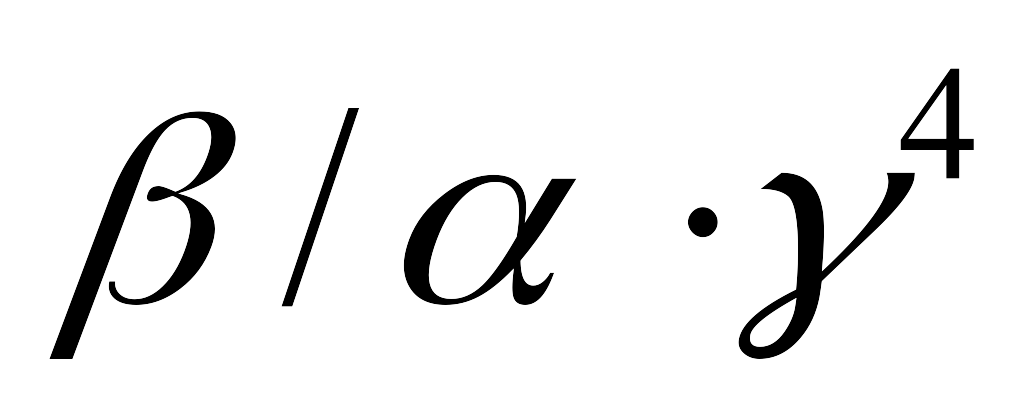раз.

Семинары 9, 10. Явления переноса

В состоянии термодинамического равновесия макроскопические параметры молекулярной системы не зависят от координат. Если система не изолирована, то макроскопические параметры (давление, температура, концентрация, электрический потенциал и др.) могут меняться от точки к точке. При наличии градиентов этих параметров в системе возникают потоки молекулярных свойств (внутренней энергии, импульса, концентрации), стремящиеся вернуть её в равновесное состояние.

34

2.4. Рассмотрим ядро со спином 1. Проекция магнитного момента этого ядра вдоль направления магнитного поля может иметь три возможных значения, а именно +_, 0 и -_. Пусть вероятность того, что  = + _ будет р, и вероятность того, что  = - _, также р.

---

а) Из условия нормировки определить вероятность того, что  = 0.

б) Вычислить  , ² , ²().

2.5. Пусть F – какая-либо аддитивная физическая величина, характеризующая систему N молекул идеального газа, так что , где f_i значение f для i-ой частицы газа. Выразить абсолютную и относительную меры флуктуаций ( и ) величины F через средний квадрат флуктуации величины f.

Примечание: Величины f и g называют статистически независимыми, если . Для них справедливо равенство .

2.6. Предположим, что твердое тело содержит N ядер, удовлетворяющих условию задачи 2.3, и их взаимодействием с другими ядрами можно пренебречь. Обозначим через М полную проекцию магнитного момента вдоль заданного направления. Выразить М и его стандартное отклонение через N, р и _, используя результаты задачи 2.5. В случае затруднения адресуем к [4].

2.7. Используя условие задачи 1.5,

а) определить, на какое среднее расстояние х от начала координат смещается радиоактивный атом за время t;

б) получить формулу для стандартного отклонения смещения (х) радиоактивного атома за время t .

11

принимает вид

. (8.6)

Для идеальных твердых тел , согласно (8.2), так как , . Кроме того,

. (8.7)

В случае моноатомных твердых тел, т.е. состоящих из одного сорта атомов, например, металлов

, (8.8)

что соответствует закону Дюлонга-Пти. Для многокомпонент-ных кристаллов различны и определяются формулой (8.6).

Достаточно мелкие частицы вещества, являющиеся, тем не менее, макроскопическими, т.е. состоящими из большого числа молекул, взвешенные в жидкости или газе, находятся в хаотическом непрерывном движении или дрожании. Такое движение называют броуновским.

Поскольку энергия броуновской частицы много меньше энергии молекул окружающей среды, и вся система находится в термодинамическом равновесии, то на каждую степень свободы броуновской частицы приходится одна и та же средняя величина энергии, равная . Различают поступательное и вращательное броуновское движение. Вращательное броуновское движение играет большую роль в измерительных приборах, накладывает определенные ограничения на максимально достижимую точность измерений реакции прибора на внешние воздействия.

З а д а ч и

8.1. Найти суммарную кинетическую энергию теплового движения всех молекул кислорода , занимающих объем V =

32

производстве и имеет следующее математическое выражение:

, (3.1)

где – число способов, которыми можно выбрать m различных предметов из n различных предметов (число сочетаний).

Для расчета среднего значения m и дисперсии необходимо вычислить <m^k>, где k = 1, 2 согласно (2.3). В силу трудоемкости вычислений подобного рода, процедура суммирования заменяется эквивалентной по результату, но более простой по форме дифференциальной процедурой:

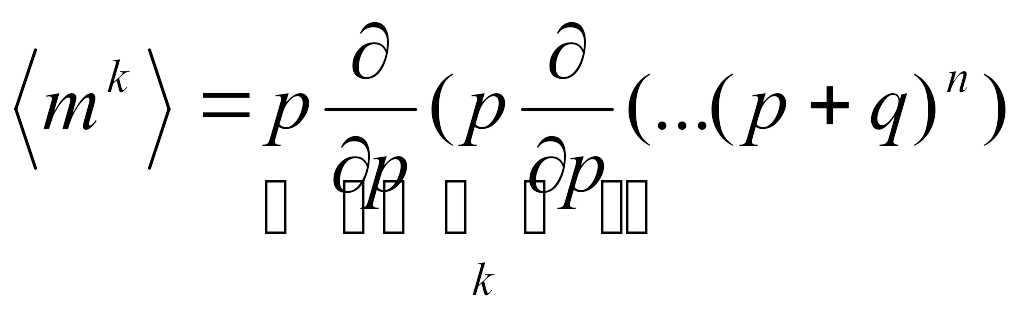. (3.2)

Существуют два важнейших предельных случая биномиального распределения.

---

Распределение Гаусса (другое его название - нормальное распределение). При и p = const, распределение плотности вероятности имеет вид

. (3.3)

В этом предельном случае m является непрерывно изменяющейся величиной (m>>1). Примерами нормального распределения являются: закон ошибок в метрологии, распределение попаданий в мишень (прицельная стрельба), распределение молекул по компонентам скорости в состоянии теплового равновесия.

Распределение Пуассона (закон редких событий).

П ри и np = const (p<<1)

(3.4)

13

7.6. Число молекул dN с координатами между r и r+dr, z и z+dz равно

,

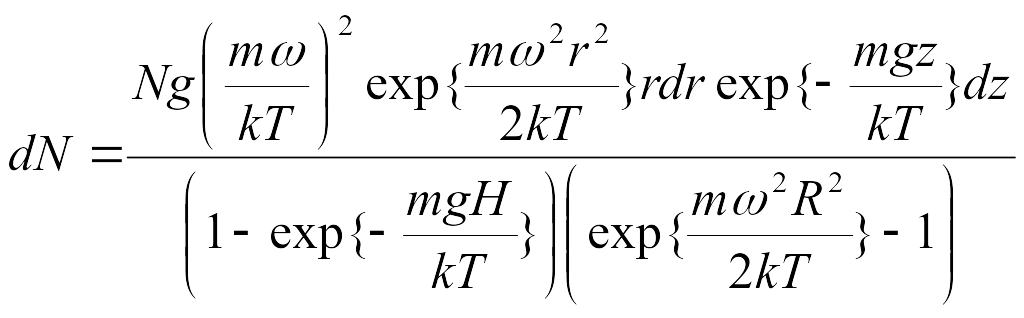где N- общее число молекул в сосуде.

Семинар 8. Равнораспределение энергии по степеням свободы. Теплоемкость многоатомных идеальных газов

и твердых тел. Броуновское движение

Число степеней свободы - это число независимых переменных, которыми определяется состояние системы. Для того чтобы полностью охарактеризовать состояние материальной точки в некоторый момент времени, необходимо задать три координаты. Для описания состояния многоатомной молекулы, содержащей N атомов, необходимо задать 3N чисел, т.е.

. (8.1)

Это полное число механических степеней свободы многоатомной системы. В молекулярной физике используют понятие статистических степеней свободы. Их число для многоатомной молекулы больше, чем число механических степеней свободы и может быть выражено через последнее. Число статистических степеней свободы равно числу квадратичных форм типа , с помощью которых записывают энергию многоатомной молекулы. Различают поступательные ( ), вращательные ( ) и колебательные ( ) степени свободы. Максимальное число статистических степеней свободы многоатомной молекулы определяют следующим образом:

30

водород вытекает из тонкостенного сосуда в вакуум. Принять температуру, при которой происходит эффузия, равной Т=300 К, давление в сосуде р=10^-6атм, площадь отверстия S=0.1 мм².

а) Показать, что количество атомов N, покидающих сосуд за

время t = 10^-3 с, подчиняется закону редких событий (p<<1).

б) Найти относительную флуктуацию потока атомов .

Примечание: число частиц эффузионного потока определяется выражением – средняя скорость теплового движения молекул,  - молярная масса газа. Давление водорода в сосуде остается постоянным.

О т в е т ы

3.1.

3.2. (применимо распределение Гаусса)

3.4.

3.5. а) p=10^-4, если объем сосуда ~ 10^-3м³;

б)

Семинар 4. Распределение Гиббса

Одной из важных проблем молекулярной физики является распределение энергии _о между различными частями изолированной системы. Совокупность незамкнутых систем, имеющих возможность обмениваться энергией только между собой, называется каноническим ансамблем. На вопрос, какова вероятность того, что система имеет некоторую энергию , при условии что _<<_о, отвечает распределение Гиббса, или каноническое распределение:

---

Смотрите также файлы

• Дискретная математика- задания.pdf

• Английский язык вопросы с ответами.pdf

• Курсовая Прочность конструкций.docx

• Экономика 11-21 Алиса.doc

• 21 Производственное освещение. Классификация производственного освещения..docx