Добавлен: 06.02.2019
Просмотров: 1045
Скачиваний: 45
, (9.1)
где In – плотность потока «меченых» частиц, D – коэффициент самодиффузии, n – концентрация «меченых» частиц.
Уравнение теплопроводности:
, (9.2)
где IQ – плотность потока внутренней энергии, - коэффициент теплопроводности, Т – температура.
Уравнение вязкости:
, (9.3)
где Imu – плотность потока импульса, - коэффициент вязкости, v – скорость слоя газа (жидкости).
Эти уравнения могут быть получены из обобщённого уравнения переноса для газов:
, (9.4)
где IG – поток молекулярного свойства G, n0 – концентрация, <v> - средняя скорость, - средняя длина свободного пробега молекул газа.
Течение газа через трубки описывается уравнениями, имеющими такую же математическую структуру, как и уравнения переноса.
Наиболее важными из них являются
а)
течение Пуазейля (для плотного газа
<<
2r),
которое описывается уравнением
35
Ответы
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
а)
б)
Семинар 3. Биномиальное распределение
Если случайное событие имеет только два исхода, причем вероятность реализации p одного из исходов в единичном испытании постоянна, то распределение вероятностей называется биномиальным. Условие нормировки в этом случае отражает альтернативный характер исхода: p + q = 1, где q – вероятность того, что событие не произошло. Биномиальное распределение отвечает на вопрос: какова вероятность реализации m определенных исходов в n независимых испытаниях при известном значении p? В статистике этот вопрос часто формулируется так: Какова вероятность обнаружить у m объектов (частиц) из n определенный признак?
Биномиальное распределение справедливо для описания случайных событий, имеющих две возможности исхода, в различных областях повседневной жизни, медицине, науке:
12
5,5 л при давлении р = 2 атм. Считать что температура газа настолько низка, что колебания атомов в молекулах еще не возбуждены, а вращения возбуждены полностью.
8.2.
Подсчитать по классической теории
удельную теплоемкость при постоянном
давлении газа следующего молярного
состава:
%,
%,
%.
Рассмот-реть два случая: а) температура
смеси такова, что колеба-тельные степени
свободы у молекул водорода не возбуждены,
а у молекул метана возбуждены полностью;
б) все степени свободы возбуждены.
8.3.
Найти значения средней энергии
,приходящейся,
согласно классической теории газов, на
одну степень свободы вращательного
движения молекулы газа при t
= 27C.
Найти значения средней квадратичной
частоты вращения молекулы кислорода
при этих условиях. Момент инерции
молекулы кислорода вокруг оси,
перпендикулярной к оси симметрии
молекулы,
.
8.4.
Удельные теплоемкости кобальта и золота
соответственно
и
.
Определить их атомные теплоемкости С1
и С2.
8.5.
Определить молярную и удельную
теплоемкости соединений: NaCl,
,
,
считая их идеальными твердыми телами.
8.6. Определить удельную теплоемкость при постоянном объеме кислорода при очень высокой температуре, когда он находится в состоянии полностью ионизированной плазмы.
8.7. Зеркальце висит на кварцевой нити, модуль кручения которой равен D. Повороты, вызванные ударами окружающих
33
Распределение
Пуассона описывает вероятности редких
событий, когда
невелико по сравнению с 1. Такими
событиями могут быть технические
катастрофы, биологические мутации,
молекулярное истечение - эффузия, вылет
частиц при радиоактивном распаде ядра.
Расчет флуктуаций в этом предельном
случае упрощается:
. (3.5)
З а д а ч и
3.1. Уровень технологии, используемый фирмой Кодак, при производстве фотопленки, гарантирует вероятность брака не выше 10-2 процентов. Каждый сотый житель города с миллионным населением раз в месяц покупает пленку Кодак. Рассчитать вероятность того, что в данном городе за месяц продадут m бракованных фотопленок Кодак (m = 0, 1, 2, 4, 10). Построить график Р(m).
3.2. Два одинаковых сосуда, в которых находится по молю одного и того же идеального газа при одинаковых условиях, сообщаются между собой через отверстие. Какое число молекул n должно перейти из одного сосуда в другой, чтобы возникшее состояние стало в = e раз менее вероятным, чем исходное?
3.3.
Воспользовавшись формулой (3.2), показать,
что <m>=pn,
.
Исходя из этого, определить стандартное
отклонение и относительную флуктуацию
величины m.
3.4. Жители города N очень любят домашних животных. В каждой семье живет либо кошка, либо собака. В городе на три кошки приходится одна собака. Сколько кошек проживает в стоквартирном доме?
3.5. Медленное истечение газа из сосуда в вакуум через отверстие, размеры которого много меньше длины свободного пробега молекул газа, называется эффузией. Газообразный
14
, 
, (8.2)
=3,
соответствующая энергия -
:
=
2 (для линейной молекулы), 3 (для нелинейной
молекулы), соответствующая энергия –
.
Энергия одномерного колебания включает
в себя кинетическую и потенциальную
составляющие:
.
На
каждую степень свободы статистической
системы приходится одна и та же средняя
энергия, равная
.
Средняя энергия многоатомной молекулы
в целом равна
. (8.3)
При
сообщении системе в некотором процессе
теплоты
ee
температура изменяется на
.
Величина, равная
,
называется теплоемкостью. Теплоемкость
единицы массы вещества называется
удельной (
),
а одного моля – молярной (
).
Молярные теплоемкости идеального газа
при постоянном объеме и давлении
связаны соотношением
. (8.4)
Молярная
теплоемкость при постоянном объеме
определена как 
,
(8.5)
учитывая,
что
,
выражение
31
где
А – нормировочная константа, g
– число микросостояний системы с
энергией
(кратность вырождения),
- параметр, определяющий термодинамическую
температуру:
, (4.2)
где
–
число доступных состояний канонического
ансамбля, посредством которых
осуществляется состояние с нулевой
энергией у рассматриваемой системы.
Формула (4.2)
дает первичное статистическое
определение температуры.
В случае
непрерывного распределения энергии
вероятность того, что система находится
в состоянии с энергией в интервале между
и
равна
(4.3)
где
dg=p(
)d
– число микросостояний, лежащих в
интервале энергий между
и
.
Величина
(4.4)
называется
плотностью состояний системы в интервале
[;
].
Статистической суммой называется величина Z:
(4.5)
В случае непрерывного распределения энергии:
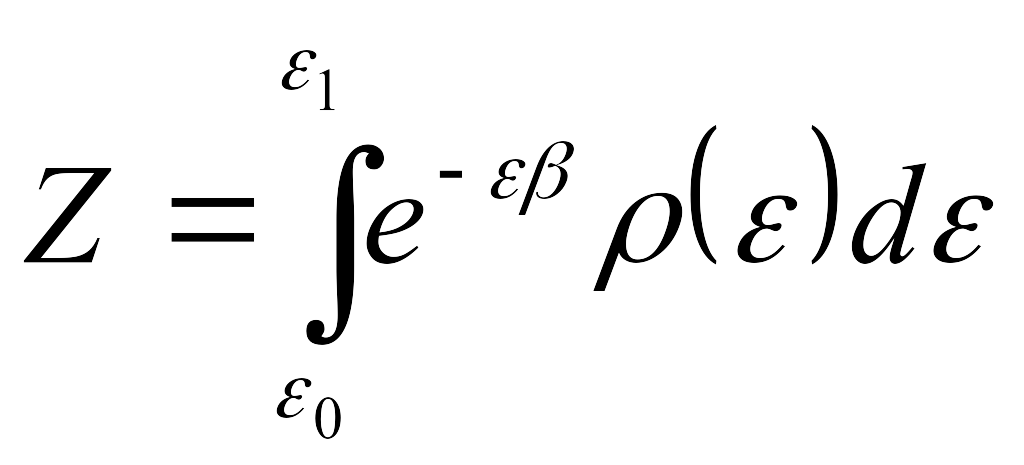(4.6)
здесь интегрирование ведется по всей области определения энергии системы.
Учитывая условие нормировки, получаем
(4.7)
16
7.4.
Для определения относительных молекулярных
масс коллоидальных частиц исследуют
распределение их концентрации в поле
центробежной силы, возникающей при
вращении центрифуги. Найти относительную
молекулярную массу
коллоидальных
частиц, если известно, что отношение их
концентраций в местах, расположенных
от оси центрифуги на расстояниях
,
равно
.
Плотности частиц -
,
растворителя -
.
Угловая скорость вращения центрифуги
.
7.5.
Найти зависимость концентрации газа
n0(0)
на оси вращения
центрифуги от ее угловой скорости
.
Построить примерный график.
7.6.
Цилиндр радиуса R
и длины H,
наполненный химически однородным газом,
равномерно вращается в однородном поле
тяжести вокруг своей геометрической
оси с угловой скоростью
.
Найти распределение молекул газа
внутри
цилиндра, если его ось направлена
вертикально.
О т в е т ы
7.1.
.
-
, -
,
.
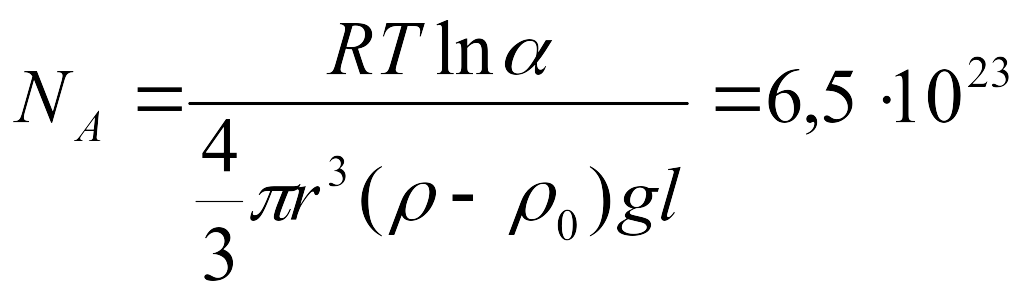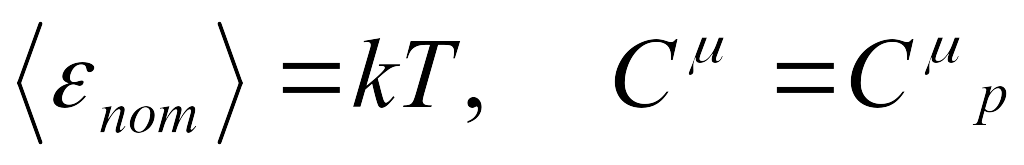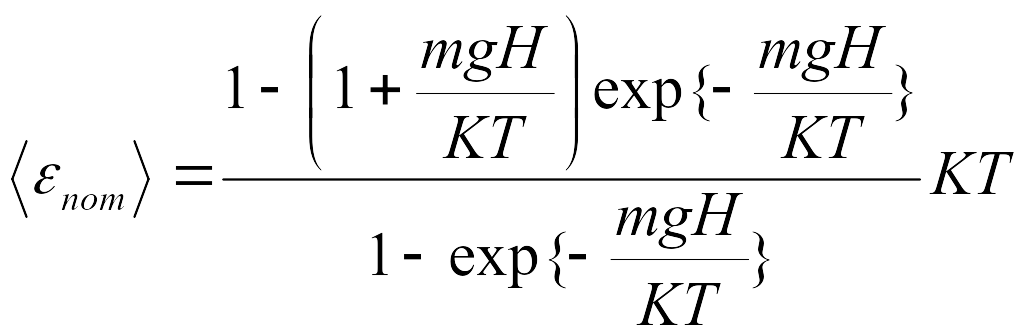7.4.
.
29
Осциллятор можно рассматривать как подсистему, находящуюся в тепловом равновесии с системой при температуре Т.
а)
Вычислить статистическую сумму такого
осциллятора. Примечание:
.
б) Рассчитать среднее значение энергии одного осциллятора.
в) Построить график зависимости средней энергии осциллятора от температуры.
г)
Получить выражение для молярной
теплоемкости
как функции от температуры. Рассмотреть
предельные случаи, когда
и
.
д)
Построить график зависимости
от температуры.
4.4.
Спин, равный 1/2, находится в контакте с
тепловым резервуаром при температуре
Т.
Спин обладает магнитным моментом
и находится во внешнем магнитном поле
В.
а) Вычислить статистическую сумму для этого спина.
б) Рассчитать среднее значение энергии спина.
в) Построить график зависимости средней энергии спина в магнитном поле.
г)
Получить выражение для молярной
теплоемкости
как функции от температуры. Рассмотреть
предельные случаи, когда
и
.
д)
Построить график зависимости
от температуры.
О т в е т ы
4.1. а) 4 %
б)
4.2.
1.4
4.3.
а)
.
18
На
основании того, что
,
из (7.2) получается выражение для
пространственной концентрации частиц
как
функции от высоты z:
, (7.3)
где
– концентрация частиц на высоте z,
-концентрация
на высоте, где потенциальная энергия
равна нулю,
– молярная масса газа, R=8,314
Дж/(мольК)
(универсальная газовая постоянная).
Выражение для
может быть получено из условия сохранения
количества частиц в газовом столбе
высотой Н
и площадью сечения S
=1
:
,
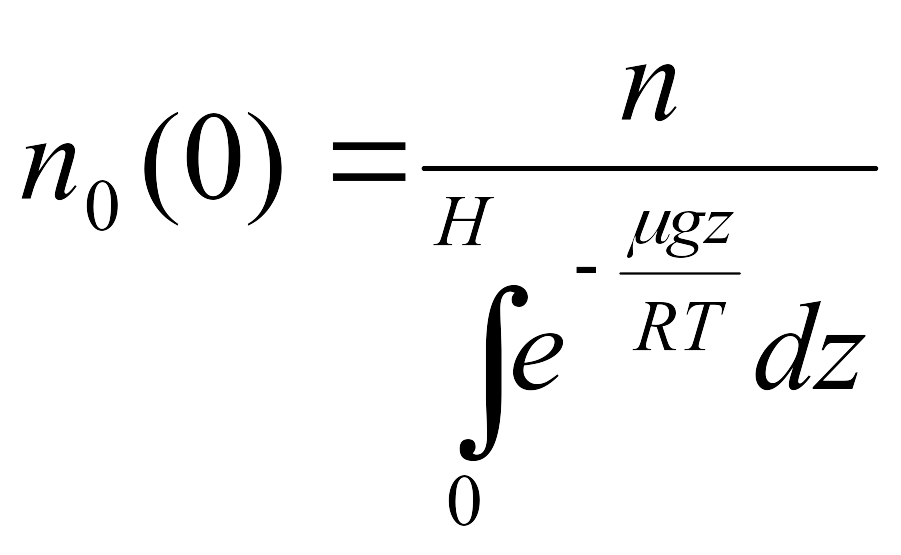. (7.4)
В
поле центробежных сил, например, во
вращающейся с угловой скоростью
центрифуге,
– потенциальная энергия молекулы
зависит от ее удаленности r
от оси вращения. В этом случае
пространственная концентрация
определяется следующим образом:
, (7.5)
где
– концентрация частиц на оси вращающегося
цилиндра. Значение этой величины можно
получить из условия сохранения полного
числа частиц в объеме
цилиндра
радиуса R
и высоты H.
. (7.6)
27
(5.2)
При решении некоторых задач удобно пользоваться распределением Максвелла по отдельным компонентам скоростей:
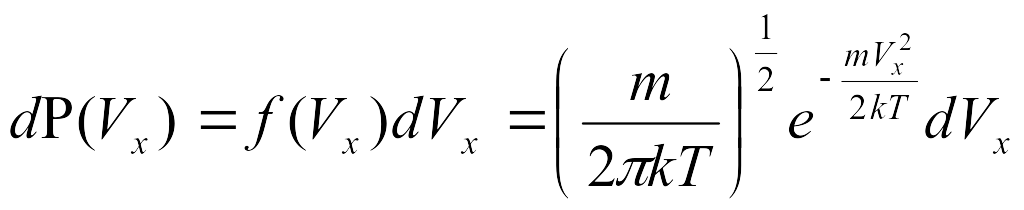(5.3)
– это
вероятность того, что значение компоненты
скорости
частицы лежит в интервале от
до
.
Аналогичные выражения справедливы для
вероятностей
и
.
Примерный вид плотности вероятности
приведен на рис.5.1.
В сферической системе координат распределение Максвелла, в случае изотропного пространства, имеет следующий вид:
. (5.4)
Оно
отвечает на вопрос какова вероятность
того, что абсолютная скорость частицы
лежит в интервале от
до
,
а также на вопрос, сколько частиц
из
имеют абсолютную скорость в заданном
интервале:
. (5.5)
Следует
отметить, что
и
– очень большие числа, но
.
Соответственно, доля частиц, имеющих
абсолютную скорость в интервале от
до
,
равна
.
(5.6)
На рис.5.2 приведен примерный вид плотностей вероятности распределения Максвелла для различных температур. Здесь же
20
(постоянная
Авогадро),
,
T=300K,
V=500
м/с,
=2
м/с, R=8,31
,
получаем
5.2. Значения всех величин равны нулю.
5.3.
.
5.4.
концентрация
идеального газа.
5.5.
a)
,
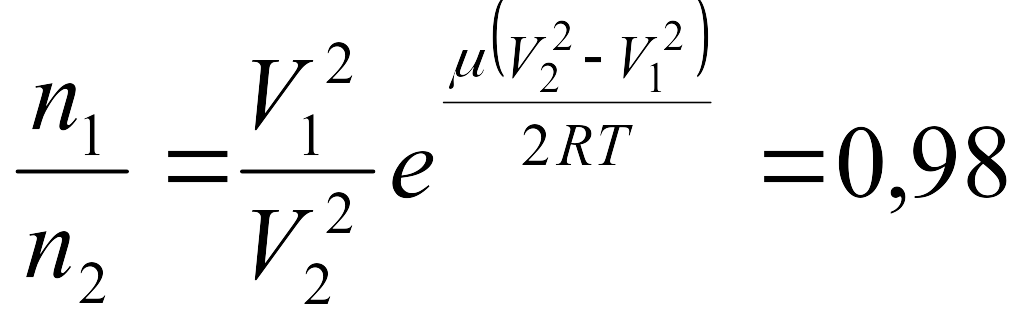б)
.
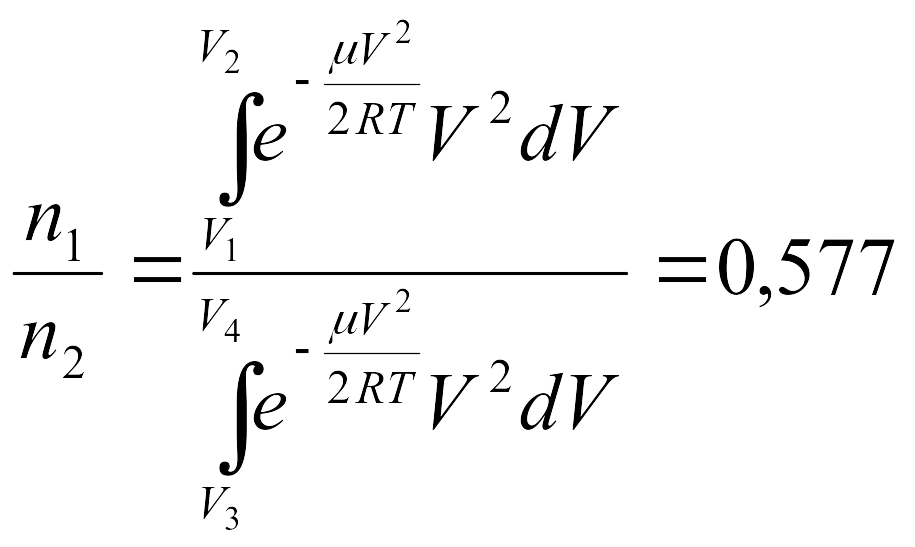5.6.
5.7.
5.8.
5.9.
5.10.
5.11.
25
Рис.5.2
. (5.8)
Среднее значение параметра, зависящего от одной компоненты скорости, вычисляется по формуле
. (5.9)
В случае, когда параметр зависит от двух или трех компонент скорости, для его усреднения следует использовать распределение (5.1).
Характерными скоростями распределения Максвелла принято называть три величины:
1.
Наивероятнейшая скорость -
.
2.
Средняя скорость -
.
3.
Средняя квадратичная скорость -
.
22
З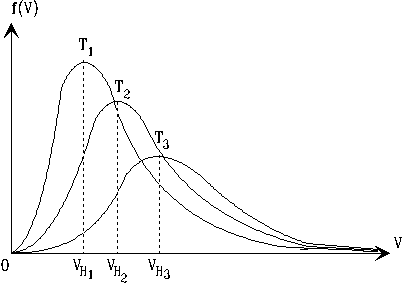
а д а ч и
5
Т1<T2<T3
T1<T2<T3
5.2. Исходя из распределения Максвелла, найти следующие величины:
,
,
.
5.3. Получить выражение для среднего квадрата x-компоненты скорости молекулы газа. Найти среднюю кинетическую энергию, приходящуюся на одну степень свободы поступательного движения молекулы газа.
5.4. Используя распределение Максвелла по одной компоненте скорости, получить выражение для давления на стенку сосуда.
5.5.
Найти отношение числа молекул
водорода
,
если температура водорода 300С:
а) число частиц
имеют скорости от 3000 м/c
до 3010 м/с, а
-
в пределах от 1500 м/c
до 1510 м/c;
б) для
интервал скоростей от 3000 м/с до 4000 м/с,
для
– от 2000 м/c
до 3000 м/c.
5.6. Получить выражения для трех характерных скоростей распределения Максвелла.
5.7. Найти среднее значение обратной величины скорости молекулы в газе.
5.8.
Написать выражение для среднего числа
молекул
газа, кинетические энергии которых
заключены между
и
.
23