Добавлен: 06.02.2019
Просмотров: 1046
Скачиваний: 45
(4.1)
15
Так
как
,
то выражение (7.6) примет вид
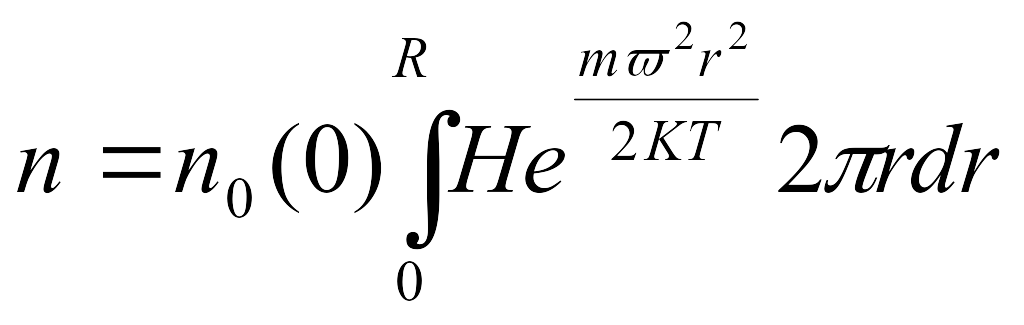, (7.7)
отсюда
получается выражение для
:
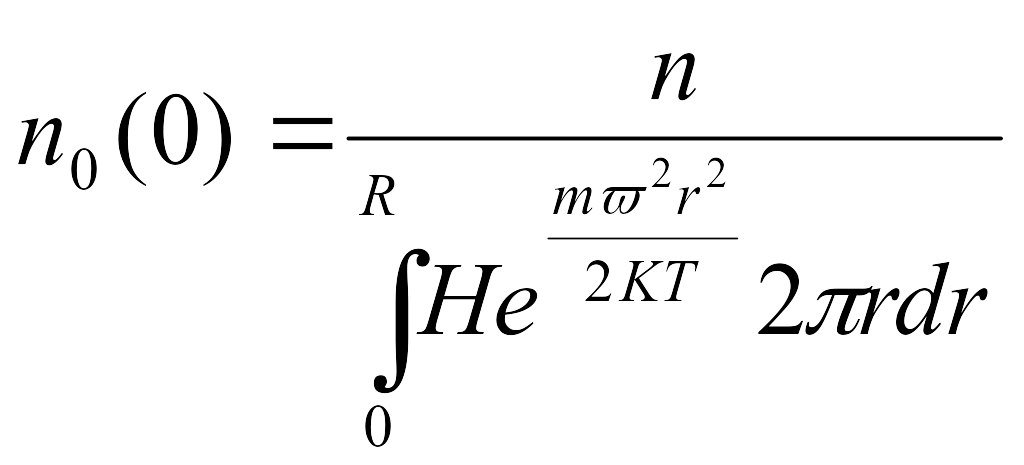. (7.8)
З а д а ч и
7.1.
Для определения числа Авогадро Перрен
измерял распределение по высоте
шарообразных частиц гуммигута, взвешенных
в воде. Он нашел, что отношение
числа
частиц в слоях, отстоящих друг от друга
на расстояние l=30 мкм, равно 2,08. Плотности
частиц
=
1,194 г/
,
воды
=1 г/
.
Радиусы частиц r = 0,212 мкм. На основании
этих данных вычислить число Авогадро.
Температура воды t=18C.
7.2. Методом статистической суммы найти среднюю потенциальную энергию молекулы воздуха в идеальной атмосфере (g=const, T=const на любой высоте). Вычислить молярную теплоемкость газа С. Считать, что молекулам газа доступна высота от нуля до бесконечности.
7.3.
В теплоизолированный цилиндрический
сосуд высоты H
помещен моль идеального газа с
относительной молекулярной массой
.
Цилиндр подвешен в вертикальном положении
в однородном поле тяжести. Температура
газа в сосуде везде одинакова и равна
T.
Найти среднюю потенциальную энергию
молекулы газа
,
теплоемкость этого газа, учитывая
влияние поля тяжести и предполагая, что
.
28
С помощью статистической суммы Z можно формализовать вычисление среднего значения энергии и ее дисперсии:
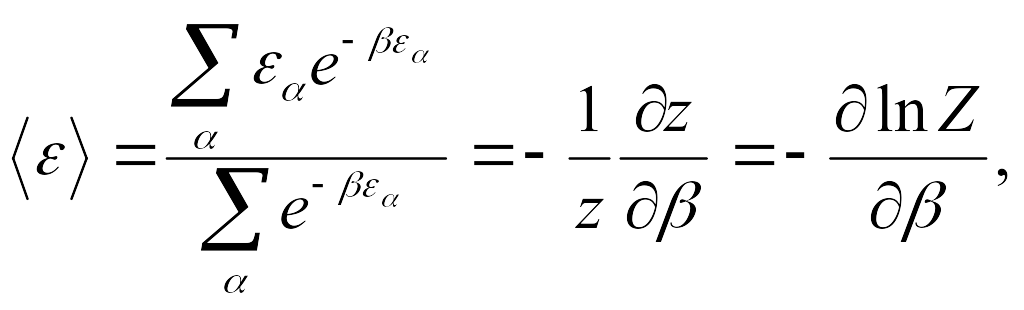(4.8)
(4.9)
З а д а ч и
4.1. Рассмотрим произвольную макроскопическую систему при комнатной температуре.
а)
Воспользовавшись определением
термодинамической температуры, найти
процентное увеличение числа микроскопических
состояний, доступных такой системе, при
возрастании ее энергии на
эВ.
б) Система поглотила единичный фотон видимого света
(
= 5
см).
Во сколько раз изменилось число доступных
системе микросостояний?
4.2. Определить отношение числа атомов газообразного натрия в состоянии 3Р к числу атомов в основном состоянии 3S
при
температуре Т=2400
К. Известно, что переходу 3Р3S
соответствует спектральная линия с
длиной волны
=589нм.
Кратности вырождения состояний 3Р
и 3S
равны соответственно 6 и 2.
4.3. Квантовый гармонический осциллятор характеризуется набором дискретных состояний с энергией
,
n
= 0,1,2,3…..,
–
частота колебаний осциллятора.
17
5.12.
5.13.
Для изотропного распределения
.
Для
распределения Максвелла
.
Семинар 7. Распределение Больцмана
Если
идеальный газ находится в силовом поле,
то его состояние может быть нестационарным,
неравновесным. Тогда распределение
Гиббса для него неприменимо. Только
некоторые потенциальные поля приводят
молекулярную систему к тепловому
равновесию и стационарному распределению
частиц в пространстве. Такими полями
являются однородное гравитационное
поле, поле центробежных сил и
электростатическое поле. В этих трех
случаях распределение Гиббса применимо.
Т.к. потенциальная энергия частицы не
зависит от ее скорости, а кинетическая
энергия не зависит от координаты частицы,
то можно рассматривать распределение
по скоростям и по координатам отдельно.
Распределение частиц по скоростям
описывается распределением Максвелла,
а пространственное распределение частиц
описывается распределением Больцмана.
В общем случае, если потенциальная
энергия частицы зависит от трех координат
-
,
то распределение Больцмана имеет
следующий вид:
(7.1).
В
однородном гравитационном поле(g=const)
потенциальная энергия частицы равна
и распределение Больцмана записывается:
. (7.2)
26
б)
г)
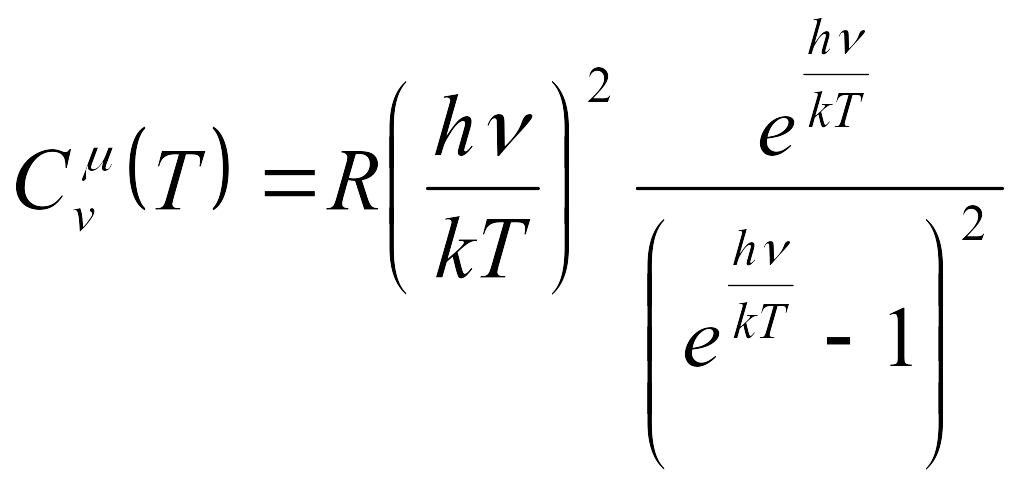
4.4.
а)
б)
г)
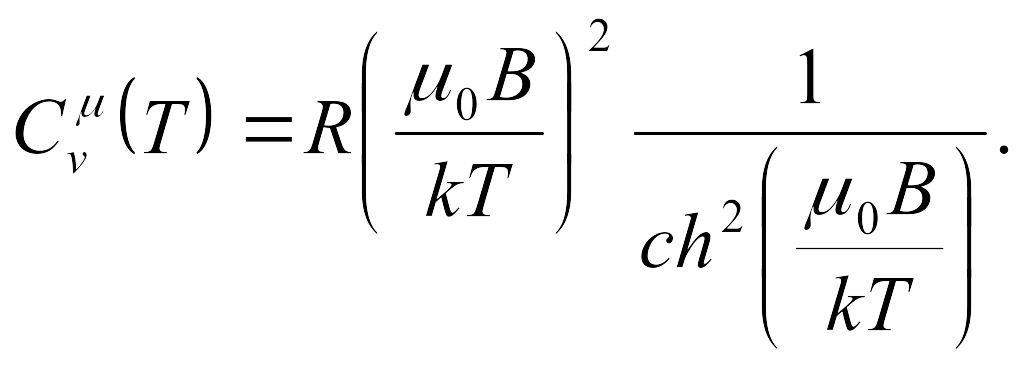
Семинары 5, 6. Распределение Максвелла
В
состоянии теплового равновесия частицы
идеального газа имеют различные
скорости, которые меняются и результате
столкновений. На вопрос какова вероятность
того, что частица обладает определенной
скоростью, отвечает распределение
Максвелла. Оно является частным случаем
распределения Гиббса, когда энергия
частицы есть только ее кинетическая
энергия:
.
В декартовой системе координат, в
пространстве скоростей
,
,
,
распределение Максвелла имеет следующий
вид:
,
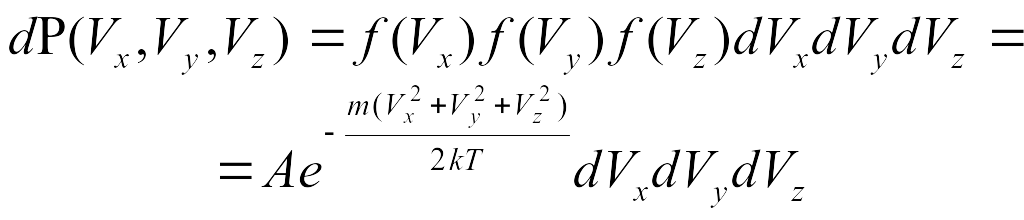(5.1)
где
- масса частицы идеального газа. Постоянная
находится из условия нормировки:
19
5.9.
Найти наивероятнейшее значение
кинетической энергии
поступательного движения молекул газа,
т.е. такое значение
,
при котором в фиксированный интервал
энергии
в
газе находится максимальное число
молекул.
5.10. Показать, что если за единицу скорости молекул газа принять наиболее вероятную скорость, то число молекул, абсолютные значения скоростей которых лежат между V и V+dV, не будет зависеть от температуры газа.
5.11.
Найти среднее число молекул, компоненты
скорости которых, параллельные некоторой
оси, лежат в интервале
,
а абсолютные значения перпендикулярной
составляющей скорости заключены между
и
.
5
Рис.5.1
5.13. Найти полную кинетическую энергию Е молекул одноатомного газа, ударяющихся о квадратный сантиметр стенки в единицу времени. Задачу решить сначала в общем виде для изотропной функции распределения, а затем применить результат к частному случаю максвелловского распределения.
О т в е т ы
5.1.
,
подставив данные
24
п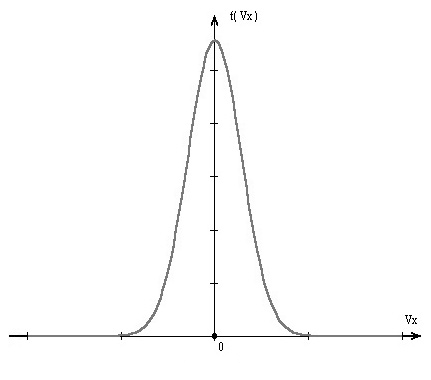
оказаны
наивероятнейшие скорости каждого
распределения. Как видно, они растут с
увеличением температуры. Их значения
можно получить, решая задачу на экстремум
функции плотности вероятности:
. (5.7)
Приведенные
формулы распределения Максвелла
позволяют находить средние значения
различных микроскопических параметров,
зависящих от скорости или ее отдельных
компонент, в соответствии с общей
процедурой усреднения. Если параметр
зависит от абсолютной скорости -
,
то его среднее значение найдется
вычислением интеграла
21
Составители О.И. Москвич, О.Ю. Селиверстова
Общая физика. Молекулярная физика: План-конспект семинарских занятий /Краснояр. гос. ун-т; сост. О.И.Москвич, О.Ю.Селиверстова. Красноярск: РИО КрасГУ, 2006. – 41 с. (Экспресс-издание)
Печатается по решению редакционно-издательского совета Красноярского государственного университета
Красноярский
государственный
университет, 2006
Москвич О.И.,
Селиверстова О.Ю.,
2006
Общая физика. Молекулярная физика
Составители Ольга Ивановна Москвич,
Оксана Юрьевна Селиверстова
Редактор И.А.Вейсиг
Оригинал-макет Г.В. Казанцевой
Подписано в печать 05.12.2006. Формат 60х84/16
Усл. печ. л.2,4. Уч.-изд. л.2,2.
Тиражируется в электронном варианте
Издательский центр
Красноярского государственного университета
660062 Красноярск, пр. Свободный,79.
«Насаждение» общей идеологии предполагает мягкий вариант прокрустова ложа и оставляет для коллег-преподавателей относительную свободу и самостоятельность, как в области методики преподавания предмета, так и в расширении содержания базы задач.
Семинар 1. Элементы теории вероятности и
физической статистики: вероятность, плотность вероятности, условие нормировки вероятности
Большинство событий в системе многих частиц (молекулярной системе) являются случайными. Закономерности, связанные со случайными величинами, изучаются теорией вероятности и математической статистикой. В теории вероятности [1,4] основным определением является частотное определение вероятности Р случайного события А:
(1.1)
где Ni – количество случаев, в которых наблюдается интересующий результат, N – общее число всех возможных случаев. Вероятность достоверного события (Ni = N) равна единице. Вероятность невозможного события равна нулю.
В статистической физике вероятностью макроскопического состояния системы называется величина Р [3,4]:
(1.2)
где Г0 – общее число микросостояний, доступных для системы, Г - число микросостояний, приводящих к данному макросостоянию . Г называют термодинамической вероятностью макроскопического состояния. Величины Г0 и Г в ряде задач могут быть вычислены с помощью методов комбинаторики. Подробный вывод основных формул элементарной комбинаторики приведен в [3].
4
О г л а в л е н и е
Введение ……………………………………………………………3
Семинар 1. Элементы теории вероятности и
физической статистики: вероятность, плотность
вероятности, условие нормировки вероятности …………… 4
Семинар 2. Средние значения физических величин
и их флуктуации ……………………………………………….9
Семинар 3. Биномиальное распределение …………………..12
Семинар 4. Распределение Гиббса …………………………. 15
Семинары 5, 6. Распределение Максвелла …………………18
Семинар 7 Распределение Больцмана ……………………….26
Семинар 8. Равнораспределение энергии по
степеням свободы. Теплоемкость многоатомных
идеальных газов и твердых тел.
Броуновское движение .………………………...……………30
Семинары 9, 10. Явления переноса …..……………………34
Справочный материал ………………..………………………….39
41
(1.8)
Знание плотности вероятности позволяет найти вероятность для любой области, в которой определена плотность.
Рис.1
На
рис.1 п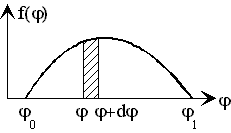
редставлен
пример графического изображения
плотности вероятности. Площадь
заштрихованной полоски на рисунке равна
вероятности dP()
нахождения величины
в интервале [;
d].
Площадь под всей кривой f()
есть вероятность нахождения величины
в интервале [0;1],
которая всегда постоянна, равна 1 или
100% и определяет условие нормировки
плотности вероятности.
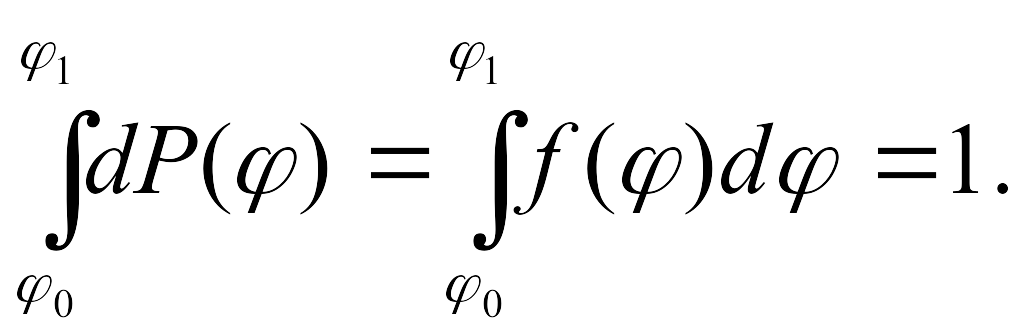(1.9)
Часто условие нормировки записывают для интервала значений [0, ∞) или (-∞, +∞), полагая, что за пределами конечного интервала [,] плотность вероятности равна нулю.
Условие нормировки вероятности дискретно изменяющейся переменной , которая может принимать n различных значений i с соответствующей вероятностью Pi , записывается так:
(1.10)
Выражения (1.9) и (1.10) являются следствием теоремы сложения вероятностей для несовместных событий [1,4].
6
9.8.
,
.
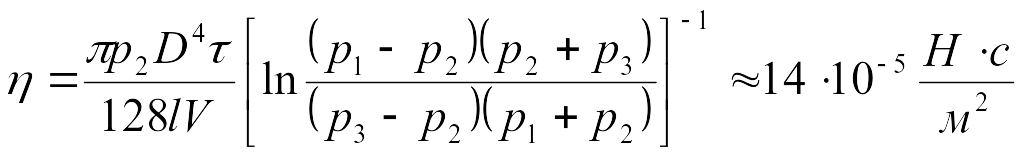Справочный материал
Постоянная Планка
.
Масса
электрона
.
Заряд
электрона
.
Число
Авогадро
.
Постоянная
Больцмана
.
Универсальная
газовая постоянная
.
Объем моля идеального
газа при нормальных условиях
.
Постоянная
Лошмидта (число молекул в одном кубическом
метре вещества, находящегося в состоянии
идеального газа при нормальных условиях)
.
(интеграл
Пуассона)
39
Найти нормировочную константу А для каждого случая. Построить соответствующие графики плотности вероятности.
1.4. Проверить выполнение условия нормировки вероятности в задаче 1.1.
1.5. Представим себе тонкую медную проволоку, натянутую вдоль оси Х. Несколько атомов меди, расположенных вблизи х=0, сделали "мечеными" (радиоактивными). При увеличении температуры нити подвижность атомов возрастает. При этом каждый атом может перескочить на соседнее место в кристаллической решетке либо направо, либо налево. Параметр решетки равен l.
Предположим, что в момент времени t=0 температура нити быстро возрастает до некоторого большого значения и в дальнейшем остается неизменной, т.е. до момента t=0 атомы "не прыгали", а покоились в узлах решетки, в том числе и "меченые" атомы в окрестности x=0.
Вероятность того, что радиоактивный атом будет обнаружен по истечении времени t при условии, что t>> ( - время нахождения атома в узлах решетки), в интервале [x, x+dx] определяется плотностью вероятности f(x), dP(x) = f(x)dx. Изобразить на графике примерный ход плотности вероятности в зависимости от x, исходя из соображений симметрии и условия нормировки, для следующих трех случаев:
а) вскоре после t=0,
б) по прошествии относительно большого времени t,
в) по прошествии очень большого времени t.
О т в е т ы
1.1.
Гm=1;
5; 10; 10; 5; 1. Г0
= 32.
1.2.
а) Pn(m)=
8
кого и цилиндрического слоёв.
9.4. Через тонкую трубку ( >> 2r) течёт ультраразреженный газ. Оценить число молекул N, ежесекундно проходящих через поперечное сечение трубки длины l, если на одном её конце концентрация молекул n1, а на другом – n2. Течение считать изотермическим.
9.5. Определить, на какой угол повернётся диск, подвешенный на упругой нити, если под ним на расстоянии h = 1 см. вращается второй такой же диск с угловой скоростью = 50 рад/с. Радиус дисков R = 10 см, модуль кручения нити f = 100 динс/см. Краевыми эффектами пренебречь. Движение воздуха между дисками считать ламинарным.
9.6. Решить предыдущую задачу в предположении, что диски помещены в сильно разреженный воздух с P = 10-4мм.рт.ст., когда молекул воздуха велика по сравнению с расстоянием между дисками. Для упрощения расчёта считать, что все молекулы движутся с одинаковыми по абсолютному значению скоростями, равными средней скорости молекул воздуха V = 450 м/с.
9.7. Определить расход массы газа Q при стационарном изотермическом пуазейлевом течении его вдоль цилиндрической трубы длины l и радиуса r, на концах которой поддерживается давление P1 и P2 (P1 > P2).
9.8. Для определения вязкости углекислого газа им наполнили колбу с объёмом V = 1 л при давлении P1 = 1600 мм.рт.ст. Затем открыли кран, позволяющий CO2 вытекать из сосуда через капилляр длиною l = 10 см и диаметром D = 0,1 мм. Через время = 22 мин давление в колбе понизилось до P3 = 1350 мм.рт.ст. Вычислить из этих данных и газокинетический
37
Абсолютной мерой флуктуации является дисперсия – средний квадрат отклонения случайной величины от ее среднего значения:
. (2.3)
Формула (2.3) может быть расписана более подробно:
а) для непрерывно изменяющейся случайной величины
; (2.4)
б) для дискретно изменяющейся случайной величины
(2.5)
Корень квадратный из дисперсии называется стандартным (среднеквадратичным) отклонением.
Мерой относительной величины флуктуации является (относительное стандартное отклонение):
(2.6)
З а д а ч и
2.1. Получить формулу (2.3) для вычисления дисперсии.
2
.2.
Фильтр радиотехнического устройства
пропускает шумы в полосе частот от
до .
Считая, что шум равномерно распределен
по частотам, построить график плотности
вероятности. Найти значения ,
и 2().
2
.3.
Рассмотрим одиночный спин, равный ½, в
магнитном поле. Его магнитный момент
с вероятностью р
может быть направлен по полю и с
вероятностью q=(1
- р) – против
поля. В
первом случае проекция магнитного момента на направление поля равна , во втором – . Определить , 2 , 2().
10
Эти процессы носят название явлений переноса. К ним, в частности, относятся диффузия, теплопроводность, вязкость. В самых простейших случаях эти явления можно описать с помощью одномерных стационарных уравнений переноса.
Уравнение самодиффузии: