ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| Институт инженерной и экологической безопасности |
| (Наименование учебного структурного подразделения) |
| 20.03.01 — Техносферная безопасность |
| (код и наименование направления подготовки / специальности) |
| Безопасность технологических процессов и производств |
| (направленность (профиль) / специализация) |
Практическое задание №2
по учебному курсу «Высшая математика»
(наименование учебного курса)
Вариант ____ (при наличии)
| Обучающегося Ю. А. Лившиц | ||
| | (И.О. Фамилия) | |
| Группа | ТБбд-2002бс | |
| | | |
| Преподаватель | Е.А. Курьянова | |
| | (И.О. Фамилия) | |
Тольятти 2023
РАЗДЕЛ № 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Задача 1
Вариант 12. Построить графики функций y= - 2x2 + 7x - 3, y ln x 1, y cos
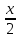 , y ln|x 1|.
, y ln|x 1|.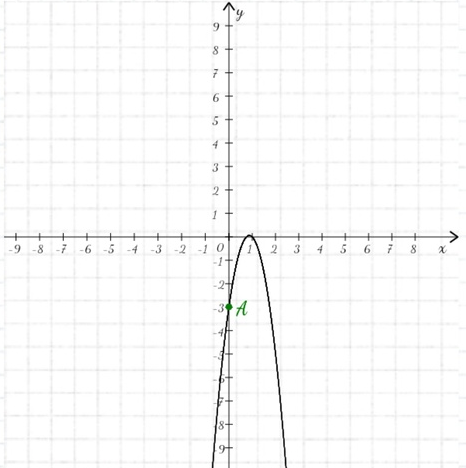
1) y= - 2x2 + 7x - 3
 2) y ln x 1
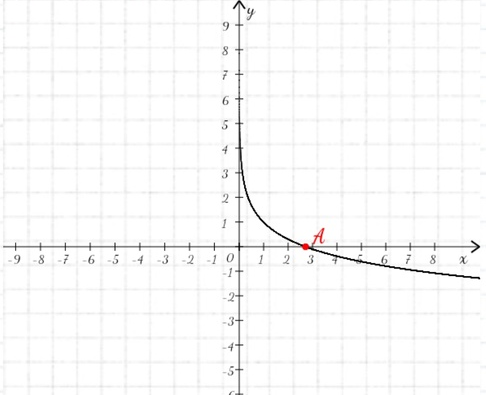
2) y ln x 1 3) y cos
3) y cos 
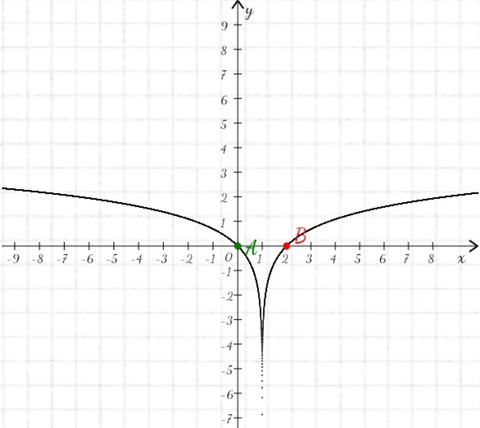 4) y ln|x 1|
4) y ln|x 1|Задача 2
Вариант 1. Записать уравнения кривых в полярных координатах и построить их.
 1) y 5x, 2) x2 + y2 =
1) y 5x, 2) x2 + y2 = 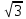 , 3) x2 + y2 = - 20x, 4) x2 + y2 = 15y
, 3) x2 + y2 = - 20x, 4) x2 + y2 = 15y1) y 5x
Вводим полярные координаты
x=r·cos φ y=r·sin φ
r≥ 0
0o ≤ φ ≤ 360o
r·sin φ=-5r·cosφ ⇒ sinφ=-5
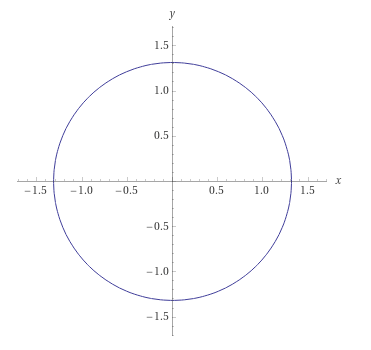
2) x2 + y2 =
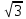
(ρ cos φ)2+( ρ sin φ)2=√3 ⇒ ρ 2·(cos2 φ +sin2 φ )=√3
ρ 2=√3
ρ = √3
ρ =4√3 – уравнение окружности с центром (0;0) и
радиусом R=4√3
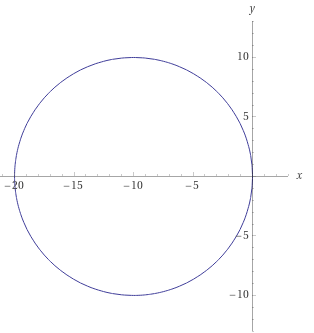
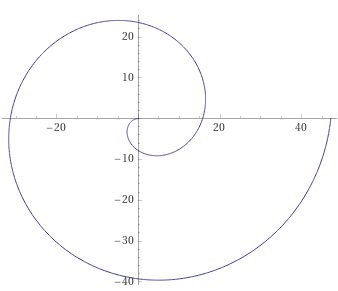
3) x2 + y2 = - 20x
x2+20x+y2=0
Выделяем полный квадрат
(x2+2·10x+102)+y2=102
(x+10)2+y2=102 – уравнение окружности
с центром (–10;0) и радиусом R=10
(ρ cos φ)2+( ρ sin φ)2=–20 ρ cos φ ⇒
⇒ρ 2·(cos2 φ +sin2 φ )=–20 ρ cos φ
ρ 2=–20 ρ cos φ
ρ=–20cos φ
ρ ≥ 0 ⇒ –20cos φ ≥ 0 ⇒ cos φ ≤ 0 ⇒
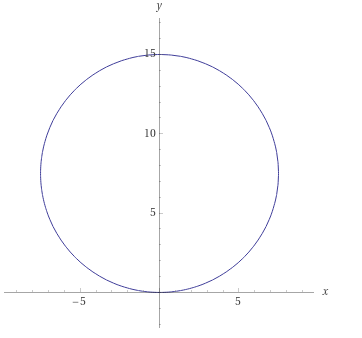
4) x2 + y2 = 15y
x2+y2–15y=0
Выделяем полный квадрат
(x2+(y2–2·7,5y+7,52) =7,52
x2+(y–7,5)2=7,52 – уравнение окружности с центром
(0;7,5) и радиусом R=7,5
(ρ cos φ)2+( ρ sin φ)2=15ρ sin φ ⇒
⇒ρ 2· (cos2 φ +sin2 φ) =15ρ sin φ
ρ 2=15ρ sin φ
ρ=15sin φ
ρ ≥ 0 ⇒ 15sin φ ≥ 0 ⇒ sin φ ≥ 0 ⇒
Задача 3
Вариант 10. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
-
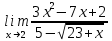 2)
2) 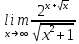 3)
3)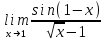 4)
4)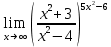
5)
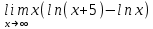
1)
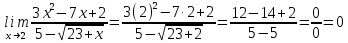
Выполняем разложение числителя на множители:
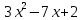
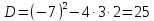
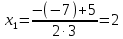
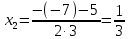
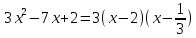
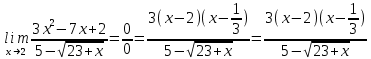
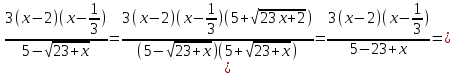
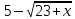
2)
 делим числитель и знаменатель на x
делим числитель и знаменатель на x 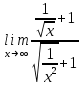
Сокращаем слагаемые
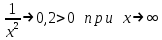
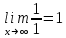
3)
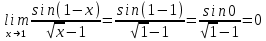
Выполним элементарные преобразования:
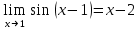
Тогда исходный предел можно представить в виде:
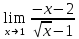
Используя свойство первого замечательного предела, выполним элементарные преобразования:
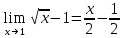
Тогда исходный предел можно представить в виде:
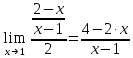
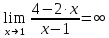
4)

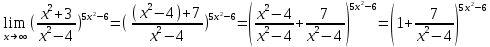
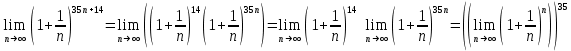
Предел
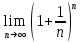 и 2 замечательный предел, который равен
и 2 замечательный предел, который равен 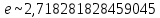 , тогда
, тогда 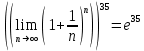
5)
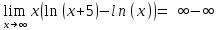
Применим формулу
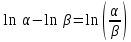 тогда
тогда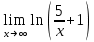
подставим значение x в функцию
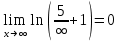
5)
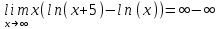
Применим формулу
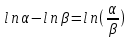 тогда
тогда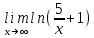 подставим значение x в функцию
подставим значение x в функцию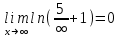
Задача 4
Вариант 12. Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.
-
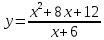 2)
2) 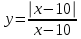 3)
3) 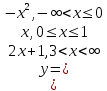
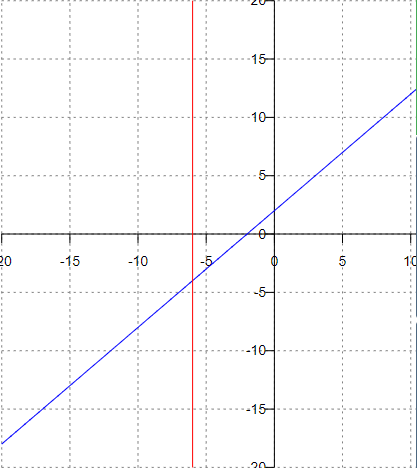 1)
1) 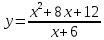
Исследуем данную функцию на непрерывность:
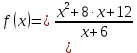
Найдем точки разрыва функции внутри указанной области. Находим переделы в точке x=-6
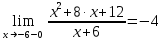
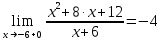
В этой точке функция имеет равные пределы, поэтому непрерывна.
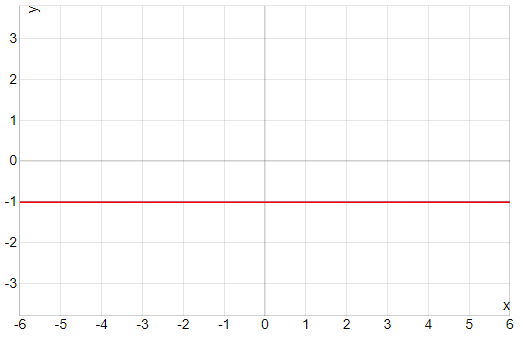 2)
2)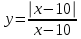
Область определения x-10≠ 0
Функция непрерывна во всех точках,
кроме х=–10
Находим предел слева, т.е. при х+10 < 0
|x-10|= –(x-10)
Тогда
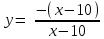
Находим переделы в точке x=10
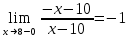
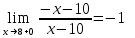
В этой точке функция имеет равные пределы, поэтому непрерывна.
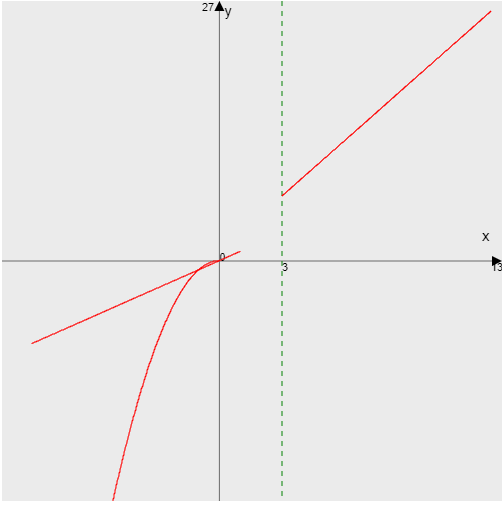 3)
3)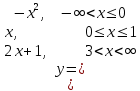
Исследуем точку стыка промежутков x=-∞
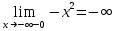
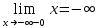
В этой точке функция терпит разрыв.
Предел равен ∞, поэтому это точка разрыва II-го рода.
Исследуем поведение функции на отрезке (-∞;1).
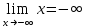
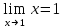
Пределы существуют, на указанном промежутке функция непрерывна.
Исследуем точку стыка промежутков x=3
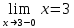
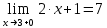
В этой точке пределы существуют, но они разные, поэтому это точка разрыва I-го рода.
Исследуем поведение функции на отрезке (3;∞).
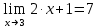

Пределы существуют, на указанном промежутке функция непрерывна.
Точка x1=-∞ является точкой разрыва II-го рода.
Точка x2=3 является точкой разрыва I-го рода.