Файл: Лабораторная работа 1 Определение места расположения распределительного склада на обслуживаемой территории. Теоретическая часть.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 355
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №1
«Определение места расположения распределительного склада на обслуживаемой территории».
1. Теоретическая часть
Задача определения места расположения распределительного центра на обслуживаемой территории может формулироваться как поиск оптимального решения или как поиск субоптимального (близкого к оптимальному) решения. Наукой и практикой выработаны различные методы решения задач обоих видов.
Задача выбора оптимального места расположения решается полным перебором и оценкой всех возможных вариантов размещения распределительных центров и выполняется на ЭВМ методами математического программирования. Однако на практике в условиях разветвленных транспортных сетей данный метод может оказаться неприменимым, так как число возможных вариантов по мере увеличения масштабов сети, а с ними и трудоемкость решения, растут по экспоненте.
Гораздо менее трудоемки субоптимальные методы определения места размещения распределительных центров. Эти методы эффективны для решения больших практических задач. Они не обеспечивают отыскивания оптимального решения, однако дают хорошие, близкие к оптимальным результаты при невысокой сложности вычислений.
1.1 Определение места расположения склада методом центра тяжести. Задание 1.
На территории района (рис.1) имеется 8 магазинов, торгующих продовольственными товарами. Методом определения центра тяжести грузопотоков найти ориентировочное место для расположения склада, снабжающего магазины.
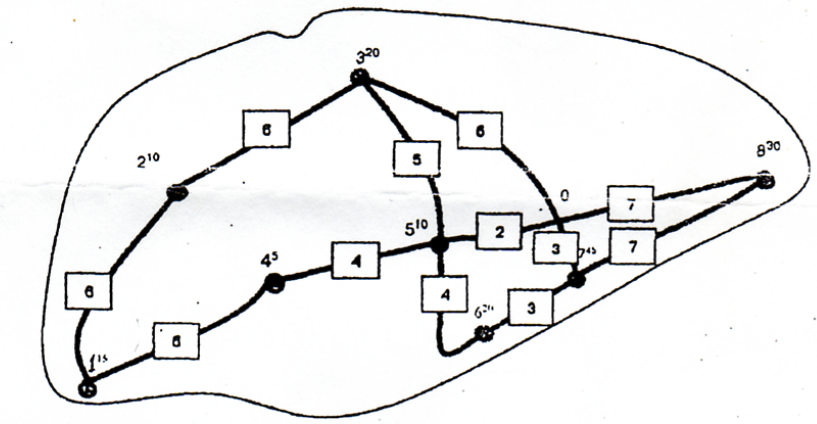
Рис. 1. Карта района обслуживания:
Методические указания к выполнению лабораторной работы.
В табл. 1 и 2 приведены координаты обслуживаемых магазинов (в прямоугольной системе координат), а также их месячный объем перевозок.
Таблица 1 - Объем перевозок и координаты обслуживаемых магазинов (Вариант №1 -8).
| № магазина | Координата Х, км | Координата Y, км | Объем перевозок, т/мес. (по вариантам) | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 1 | 10 | 10 | 15 | 10 | 45 | 10 | 20 | 10 | 10 | 15 |
| 2 | 23 | 41 | 10 | 15 | 5 | 15 | 15 | 10 | 15 | 5 |
| 3 | 48 | 59 | 20 | 40 | 10 | 20 | 10 | 15 | 20 | 20 |
| 4 | 36 | 27 | 5 | 20 | 15 | 25 | 20 | 20 | 5 | 25 |
| 5 | 60 | 34 | 10 | 10 | 20 | 30 | 25 | 30 | 15 | 30 |
| 6 | 67 | 20 | 20 | 5 | 30 | 5 | 30 | 25 | 25 | 40 |
| 7 | 81 | 29 | 45 | 30 | 10 | 10 | 5 | 5 | 20 | 45 |
| 8 | 106 | 45 | 30 | 25 | 15 | 20 | 10 | 30 | 40 | 15 |
Таблица 2 - Объем перевозок и координаты обслуживаемых магазинов (Вариант №9 -16).
| № магазина | Координата Х, км | Координата Y, км | Объем перевозок, т/мес. (по вариантам) | |||||||
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |||
| 1 | 10 | 10 | 15 | 20 | 45 | 40 | 25 | 15 | 20 | 10 |
| 2 | 23 | 41 | 15 | 35 | 5 | 15 | 15 | 10 | 15 | 5 |
| 3 | 48 | 59 | 10 | 30 | 15 | 50 | 15 | 15 | 10 | 10 |
| 4 | 36 | 27 | 25 | 20 | 15 | 25 | 20 | 15 | 5 | 25 |
| 5 | 60 | 34 | 25 | 10 | 15 | 35 | 25 | 30 | 20 | 15 |
| 6 | 67 | 20 | 20 | 10 | 30 | 5 | 40 | 15 | 25 | 35 |
| 7 | 81 | 29 | 45 | 30 | 45 | 20 | 5 | 5 | 15 | 45 |
| 8 | 106 | 45 | 15 | 20 | 15 | 20 | 10 | 30 | 40 | 40 |
Пользуясь приведенными в теоретических пояснениях к заданию формулам
, необходимо найти координаты точки (Хсклад, Yсклад), в окрестностях которой рекомендуется организовать работу распределительного склада, а также указать эту точку на чертеже.
Прежде чем приступить к расчетам, необходимо выполнить чертеж к зданию. Для этого следует нанести координатные оси, а затем точки, в которых размещены магазины. Рекомендуемый масштаб: одно миллиметровое деление – 1 км.
Задачу выбора места расположения склада решим для распределительной системы, включающей один склад. Основным (но не единственным) фактором, влияющим на выбор места расположения склада, является размер затрат на доставку товаров со склада. Минимизировать эти затраты можно, разместив склад в окрестностях центра тяжести грузопотоков.
В качестве примера решения задачи рассмотрим распределительную систему, обслуживающую четырех потребителей. Нанесем на нашу карту координатные оси таким образом, чтобы обслуживаемый район разместился в первой четверти системы координат (рис. 2). Найдем координаты точек, в которых расположены магазины – потребители материального потока.
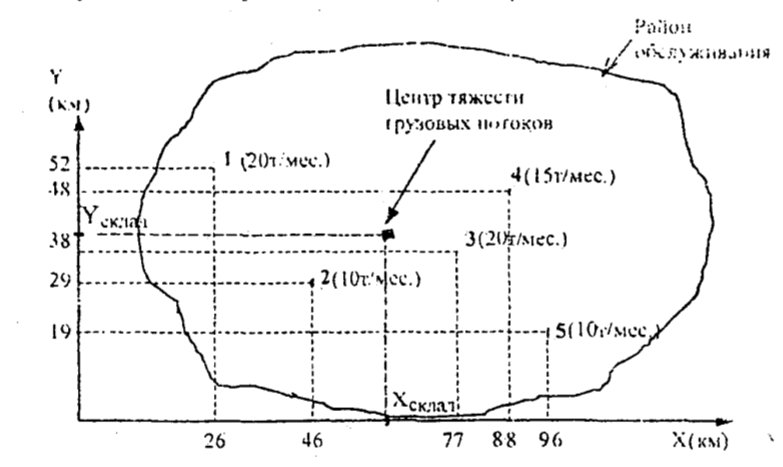
Рис. 2. Определение места расположения склада методом поиска центра тяжести грузовых потоков (в скобках рядом с номером магазина указан его месячный объем перевозок).
Координаты центра тяжести грузовых потоков (Хсклад, Yсклад), т.е. точки, в окрестностях которой может быть размещен распределительный склад, определятся по формуле:
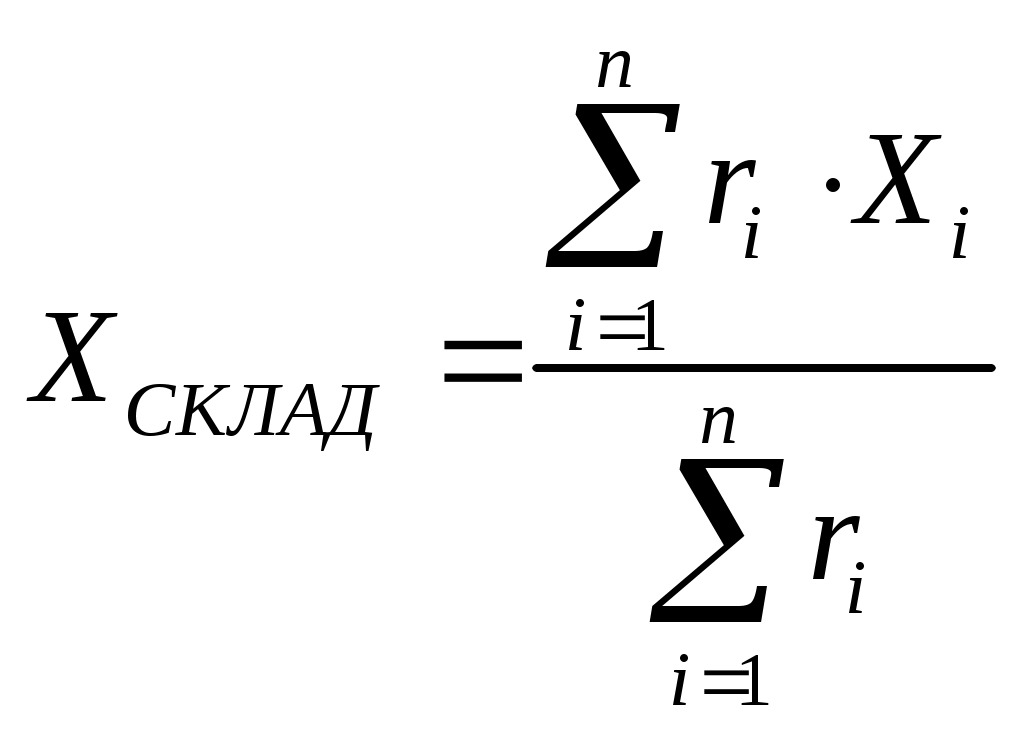 (1)
(1)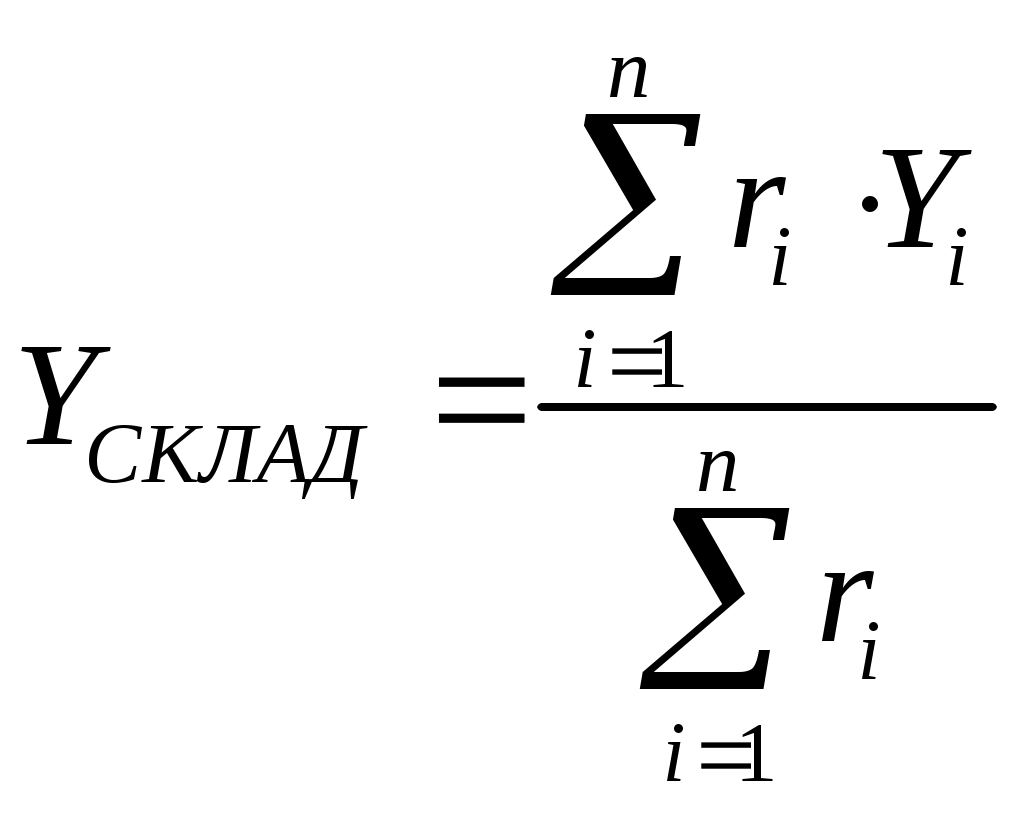 (2)
(2)где r1 – Объем перевозок i-го потребителя; Х1 Y1- координаты i-го потребителя; n – число потребителей.
Применение описанного метода имеет ограничение. На модели расстояние от пункта потребления материального потока до места размещения распределительного центра учитывается по прямой. В связи с этим моделируемый район должен иметь развитую сеть дорог, так как в противном случае будет нарушен основной принцип моделирования – принцип подобия модели и моделируемого объекта.
1.2 Определение места расположения склада методом пробной точки.
Задание 2.
На территории района (рис.1) имеется 8 магазинов, торгующих продовольственными товарами. Определите узел транспортной сети прямоугольной конфигурации, в которой размещение распределительного склада обеспечить минимум грузооборота транспорта по доставке грузов в обслуживаемую сеть.
Методические указания
Задание выполняется на чертеже, сделанном при выполнении задания 1. Изучив следующие теоретические пояснения к заданию 2, найдите и укажите на чертеже рекомендуемую точку размещения склада (точка М). Основой выполнения задания 2 является изучение метода определения оптимального места размещения распределительного склада в случае прямоугольной конфигурации сети автомобильных дорог (метод пробной точки).
Сначала на примере отдельного участка транспортной сети разберем суть метода. Пусть на участке дороги, длиной 30 км (участок AD на рис. 3), имеем четыре потребителя материального потока: A, B, C и D. Месячный объем перевозок каждого из них указан в скобках. Оптимальное место расположения распределительного склада легко определить методом, который можно назвать как «метод пробной точки».

Рис. 3. Определение оптимального места расположения распределительного склада на участке обслуживания
Суть метода состоит в последовательной проверке каждого отрезка обслуживаемого участка. Введем понятие пробной точки отрезка, а также понятия левого и правого объема перевозок пробной точки.
Пробной точкой отрезка назовем любую точку, находящуюся на этом отрезке и не принадлежащую его концам (т.е. пробная точка не совпадает с точками A, B, C и D).
Левый объем пробной точки – объем перевозок потребителей, расположенных на всем участке обслуживания слева от пробной точки.
Правый объем пробной точки – объем перевозок потребителей, расположенных справа.
Участок обслуживания проверяют с крайнего левого конца. Сначала анализируют первый отрезок участка (в нашем случае – отрезок АВ). На данном отрезке ставится пробная точка и подсчитывается сумма грузооборотов потребителей, находящихся слева и справа от поставленной точки. Если грузооборот потребителей, находящихся справа, больше, то проверяется следующий отрезок. Если меньше, то принимается решение о размещении склада в начале анализируемого отрезка.
Проверка пробных точек продолжается до тех пор, пока не появится точка, для которой сумма объемов перевозок потребителей с левой стороны не превысит сумму объемов перевозок потребителей с правой стороны. Решение принимается о размещении склада в начале этого отрезка, т.е. слева от пробной точки. В нашем примере – это точка С.
Рассмотрим вариант, когда сумма объемов перевозок слева и справа от пробной точки очередного отрезка становится одинаковой. Начало этого отрезка (точка М, рис. 4), является первым, а конец (точка N) последним из возможных мест расположения распределительного склада на участке обслуживания. Распределительный центр может быть расположен в любой из точек отрезка MN участка обслуживания.

Рис. 4. Определение оптимального расположения распределительного склада при равенстве «левого» и «правого» объемов перевозок пробной точки
Для определения методом пробной точки оптимального узла прямоугольной транспортной сети (для размещения распределительного склада) следует нанести на карту района координатные оси, сориентированные параллельно дорогам. Определив координаты потребителей, необходимо на каждой координатной оси найти методом пробной точки оптимальное место расположения координаты X и координаты Y искомого узла.
В качестве примера рассмотрим обслуживаемую систему, состоящую из 4 потребителей (рис. 5). Сеть дорог прямоугольная. Присваивая ординатам и абсциссам потребителей соответствующие значения объемов перевозок, найдем методом пробной точки ординату и абсциссу оптимального узла транспортной сети. Размещение распределительного склада в найденном узле обеспечит минимальный грузооборот по доставке товаров со складов.
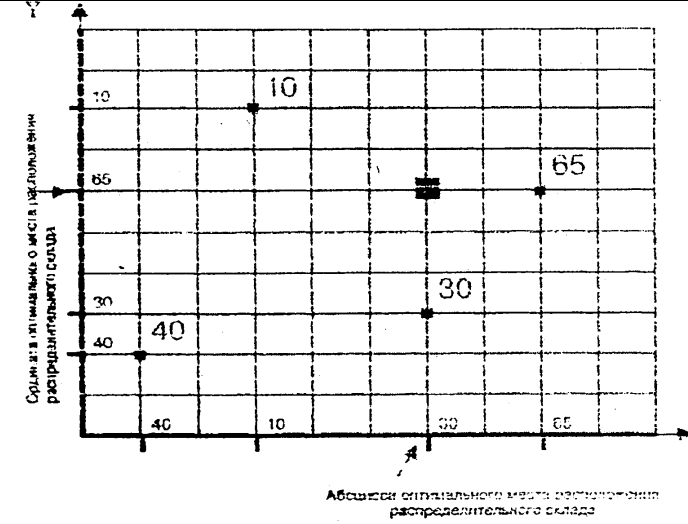
Рис. 5. Определение оптимального места расположения распределительного склада в условиях прямоугольной сети автомобильных дорог:
Точками на схеме обозначены потребители материального потока, числами – объем перевозок потребителей, т/мес.
1.3 Определение места расположения склада методом частичного перебора. Задание 3.
На территории района (рис. 1) имеется 8 магазинов, торгующих продовольственными товарами. Методом частичного перебора найти узел транспортной сети, рекомендуемый для размещения склад, снабжающего магазины.