Файл: Лабораторная работа 4 По теме Численное интегрирования по дисциплине Численные методы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 13

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»
Кафедра «Информатика»

Лабораторная работа №4
По теме

«Численное интегрирования»
по дисциплине

«Численные методы»

Выполнил: студент гр. БИК2106 Михайлов А.В.

Вариант №13
Проверил: _________

Москва, 2023 г.

1. Задание для численного интегрирования

F(x) = (5 e-x + 4 x + x3/3) – подынтегральная функция, a= -1 и b=3 – пределы интегрирования, методы интегрирования для выполнения задания – средних прямоугольников и трапеций, а начальный шаг интегрирования h0=1.

2. Ручной расчет интеграла

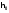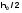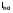Рассчитаем интеграл с шагом =1 и ( и 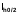), и оценка его погрешности по правилу Рунге, при использовании MathCad

Рассмотрим вычисление интеграла

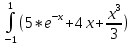
с шагом h0 = 1 и 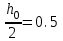методами средних прямоугольников и трапеций

Правило Рунге применяют для вычисления погрешности путём двойного просчёта интеграла с шагами h/2 и h, при этом погрешность вычисляется по формуле 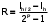. Считается, что интеграл вычислен с точностью Е, если 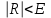, тогда 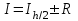, где I – уточненное значение интеграла
, p – порядок метода.

Вычислим 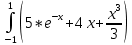с шагом h0=1 и по формулам:

  1. Средних прямоугольников и оценим погрешность интегрирования методом двойного просчёта:



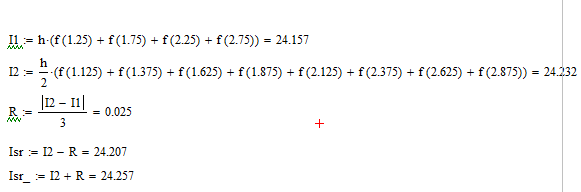
Рисунок 1 – Расчеты методом средних прямоугольников


  1. Трапеций и оценим погрешность интегрирования методом двойного просчета:



Рисунок 2 – Расчеты методом трапеций

Смотрите также файлы