Файл: Курсовая работа по дисциплине Общая теория связи Вариант 17 студент группы бин2107 Рукавицын М. Д.docx

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

Кафедра общей теории связи

КУРСОВАЯ РАБОТА

по дисциплине «Общая теория связи»

Вариант №17

Выполнил: студент группы БИН2107 Рукавицын М.Д.

Проверил: доцент кафедры ОТС
Терехов А.Н.

Москва 2023

Оглавление

Исходные данные:
Таблица 1 Исходные данные

№ в групповом журнале

ИС, АЦП; L=8

ПДУ

НКС

ПРУ

Функция корреляции сообщения BA(τ)

PA, В2

α, с-1

способ передачи

частота, МГц

G0, Вт*с

h02

способ приёма

f0

F1

17

3.4

21

ЧМ

2.6

2.65

0.0015

11

КП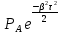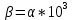

,

В условии:

P_A=σ_A² – мощность сообщения

β – показатель затухания функции корреляции

L – число уровней квантования

G₀ – постоянная энергетического спектра шума НКС

h₀² – отношение сигнал/шум (ОСШ) по мощности на выходе детектора

АМ – амплитудная модуляция

НП – некогерентный приём


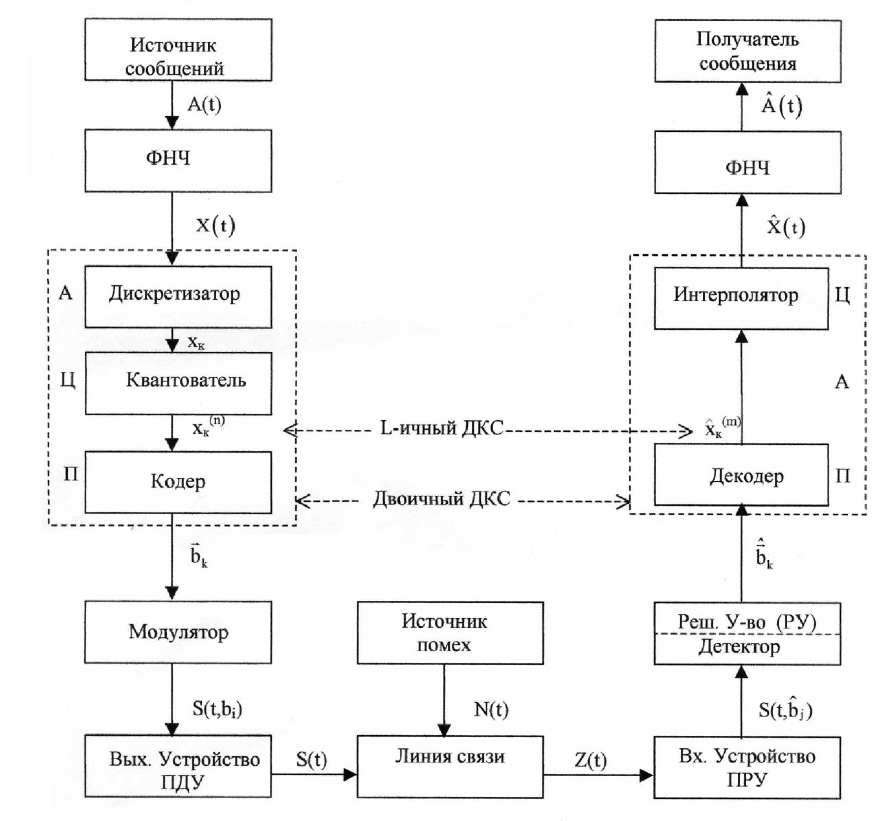
Рисунок 1 - Структурная схема системы электросвязи

Источник сообщения – некоторый объект или система, информацию о состоянии которой необходимо передать

A(t) – сообщение, несущее в себе новую информацию о состоянии источника

ФНЧ – ограничивает спектр сообщения некоторой частотой F_B

АЦП – аналогово-цифровой преобразователь, в состав которого входят:

Дискретизатор – устройство, представляющее отклик ФНЧ в виде отсчётов x_k

Квантователь – устройство, преобразующее отсчёты в квантованные уровни x_k⁽ⁿ⁾; k=0,1,2..; n=0,L; L – число уровней квантования

Кодер – устройство, преобразующее квантованные уровни в последовательность ИКМ b_k⁽ⁿ⁾

Модулятор – устройство, формирующее сигнал, амплитуда, фаза или частота которого меняется в соответствии с сигналом b_k⁽ⁿ⁾

Выходное устройство ПДУ – осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений, и обеспечения требуемого соотношения сигнал/шум на входе приёмника

Линия связи – среда или технические сооружения, по которым сигнал поступает от передатчика к приёмнику. В линии связи на сигнал налагается помеха.

Входное устройство ПРУ – осуществляет фильтрацию принятой смеси сигнал + шум

Детектор – преобразует принятый сигнал в ИКМ b_k⁽ⁿ⁾

ЦАП – цифро-аналоговый преобразователь, включающий:

Декодер – преобразует кодовые комбинации в импульсы

Интерполятор и ФНЧ – устройства, восстанавливающие непрерывный сигнал из импульсов – отсчётов

Получатель – объект или система, которому передаётся информация

Временные диаграммы


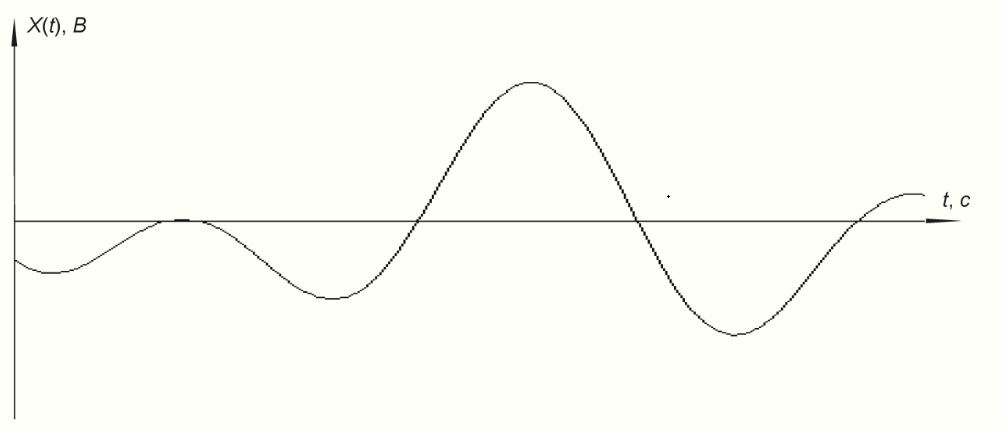
Рисунок 2 - Исходное сообщение



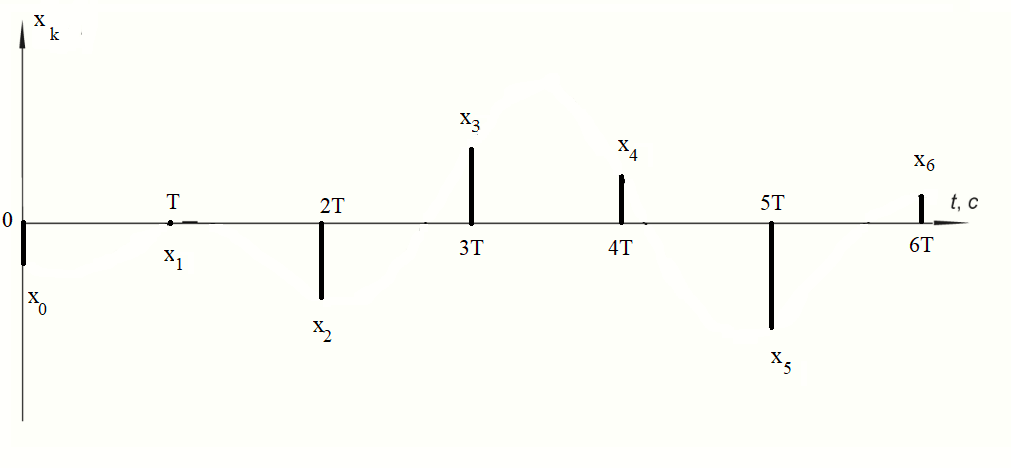
Рисунок 3 - Сигнал на выходе дискретизатора


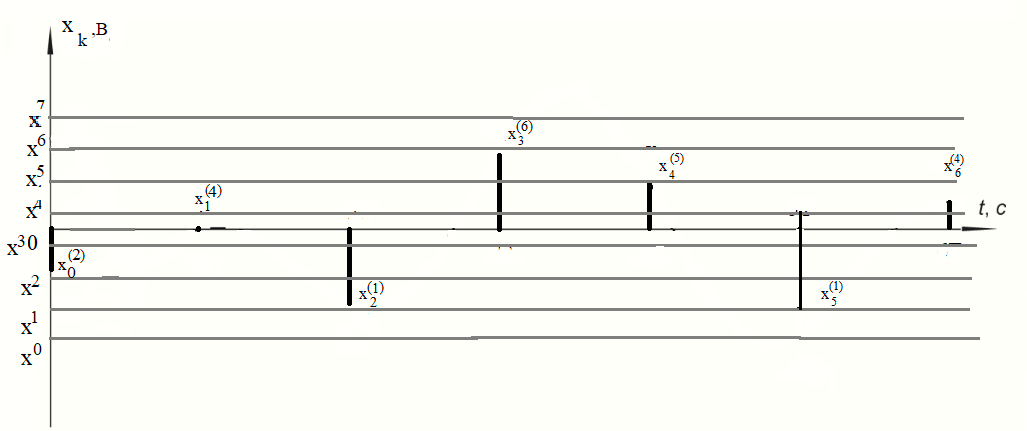
Рисунок 4 - Сигнал на выходе квантователя

Сигнал на входе кодера



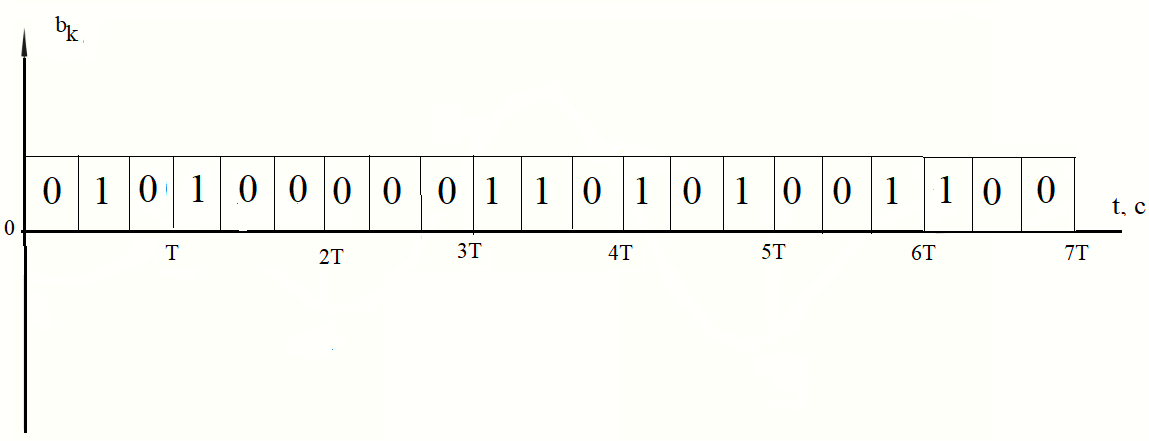
Рисунок 5 - Сигнал на выходе кодера


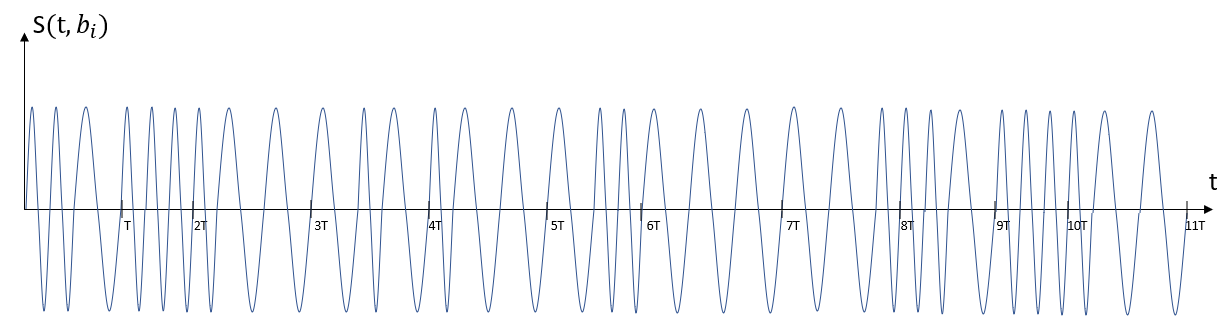
Рисунок 6 - Сигнал на выходе модулятора


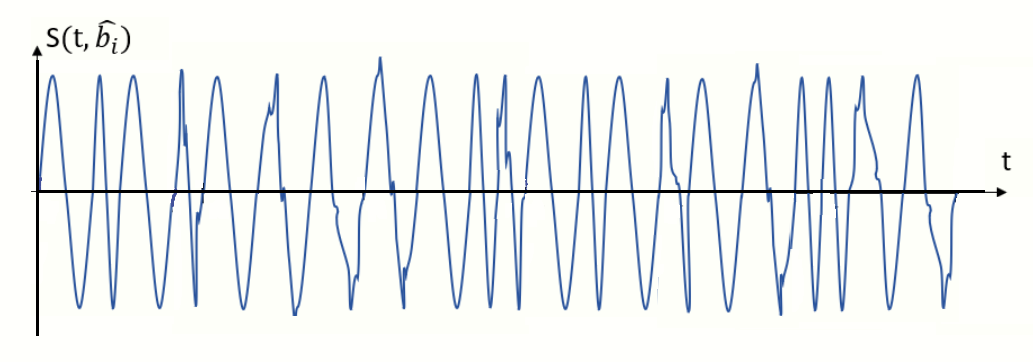
Рисунок 7 - Выход входного устройства (ПРУ) – вход детектора

В линии связи на сигнал накладывается помеха

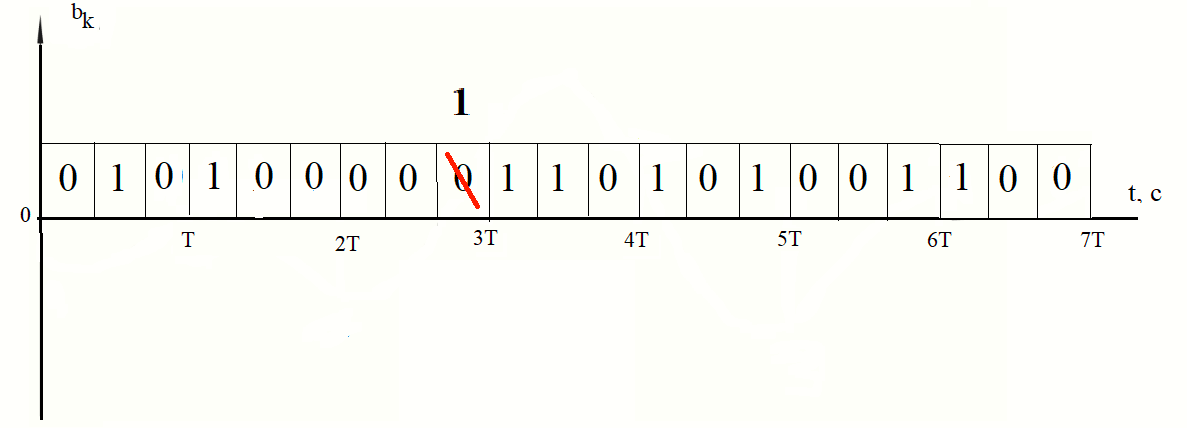
Рисунок 8 - Выход решающего устройства


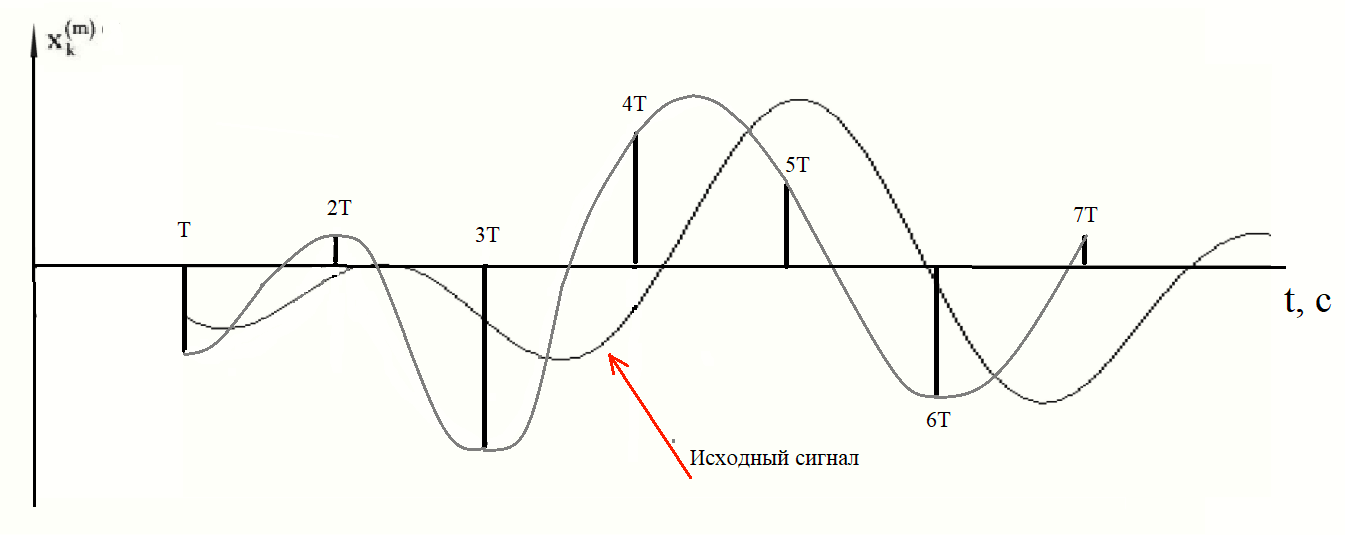
Рисунок 9 - Выход декодера

Все квантованные уровни сдвигаются на период

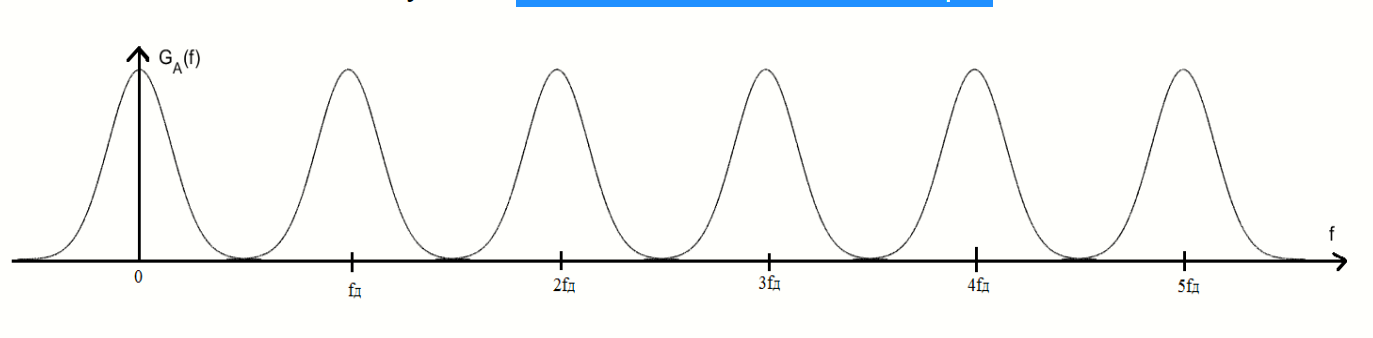
Рисунок 10 - Спектр сигнала на выходе дискретизатора

1. По заданной функции корреляции исходного сообщения:

а) рассчитать интервал корреляции, спектр плотности мощности, начальную энергитическую ширину спектра сообщения.

Рассчитаем интервал корреляции:


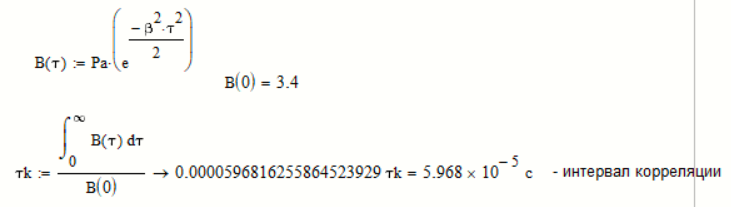
Рассчитаем энергетический спектр или спектр плотности мощности:


Найдем начальную энергетическую ширину спектра сообщения.


Для нахождения 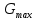возьмем производную от 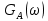и приравняем ее нулю.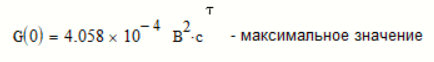

б) построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в пункте а) параметры.


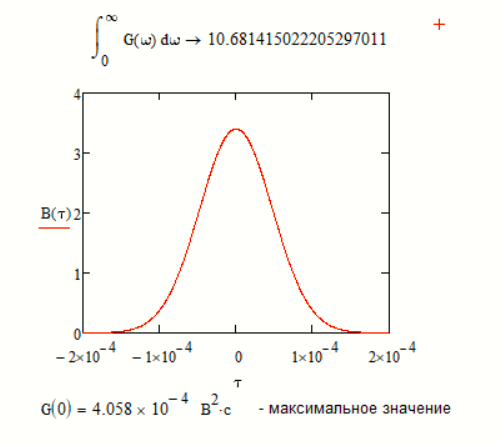
Рисунок - График функции корреляции



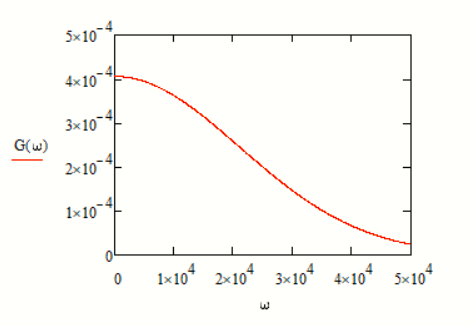
Рисунок - График спектра мощности

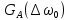
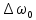
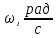
2. Считая, что исходное сообщение воздействует на идеальный фильтр нижних частот (ИФНЧ) с единичным коэффиииентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения:

а) рассчитать среднюю квадратическую погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ;

Мощность отклика ФНЧ равна:


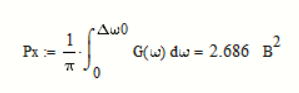
Средняя квадратическая погрешность фильтрации:


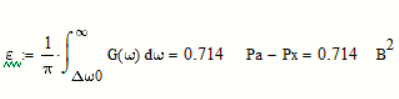
Найдем частоту и интервал временной дискретизации отклика ИФНЧ:

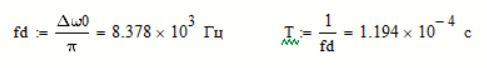
3. Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:

а) Рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК);

Рассчитаем шаг квантования:





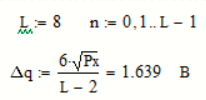
Пороги квантования находим из выражения:


Уровни квантования определяются следующими соотношениями:

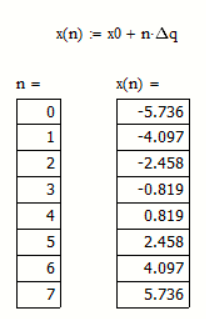
Средняя квадратическая погрешность квантования (мощность шума квантования) равна:

соответственно мощности (дисперсии) входного и выходного сигналов квантователя, а коэффициент взаимной корреляции между этими сигналами.






б) построить в масштабе характеристику квантования



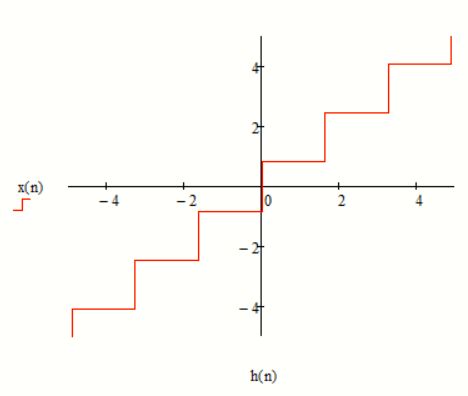
Рисунок - Характеристика квантования

4. Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L- ичного дискретного канала связи (ДКС):

а) рассчитать закон и функцию распределения вероятностей квантованного сигнала, а также энтропию, производительность и избыточность L- ичного дискретного источника;
Распределение вероятностей рассчитывается так:





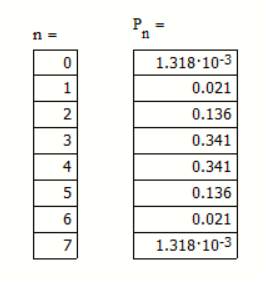
Интегральное распределение вероятностей:



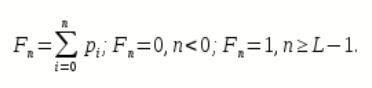
Рассчитаем энтропию.



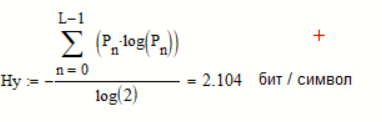
Производительность в ДКС определяется соотношением:



Избыточность последовательности источника:





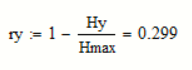
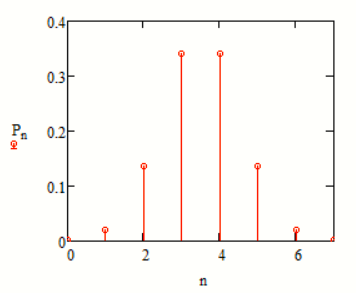
б) построить в масштабе графики рассчитанных закона и функции распределения вероятностей.

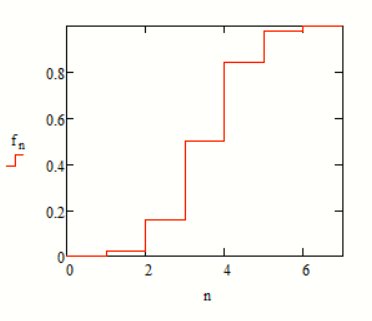
5. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода;

При организации цифровой связи широкое распространение получило двоичное кодирование, когда кодовые символы принимают только два значения 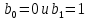. Процедура кодирования состоит в следующем.

Физические уровни 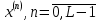, вначале пронумеровываются, т.е. заменяются их номерами 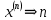. Затем эти десятичные числа представляются в двоичной системе счисления с основанием 2. Это представление имеет вид: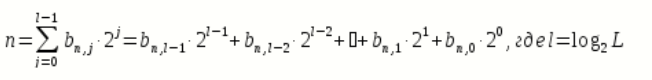


двоичный кодовый символ (0 или 1) десятичного числа 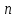, расположенный в j-ой позиции кодовой комбинации



В нашем случае



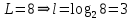
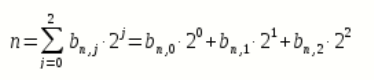
Тогда получаем:









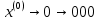
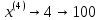
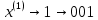
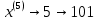
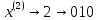
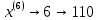
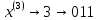
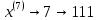
Образуется сигнал импульсно-кодовой модуляции (ИКМ)

Кодовым расстоянием 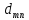между двумя двоичными кодовыми комбинациям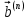и и 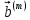называют количество позиций, в которых одна кодовая комбинация отличается от другой

Таблица кодовых расстояний:

	000	001	010	011	100	101	110	111
000	0	1	1	2	1	2	2	3
001	1	0	2	1	2	1	3	2
010	1	2	0	1	2	3	1	2
011	2	1	1	0	3	2	2	1
100	1	2	2	3	0	1	1	2
101	2	1	3	2	1	0	2	1
110	2	3	1	2	1	2	0	1
111	3	2	2	1	2	1	1	0

а) рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ:

Т.к. среднее число нулей 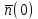и среднее число едениц 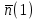в сигнале ИКМ одинаково, то и вероятность их появления одинаковы: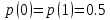



Ширина спектра сигнала ИКМ равна:

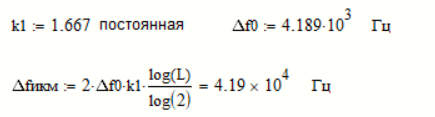
6. Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик:

а) рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра;

Сигнал ДЧМ представляется в виде:



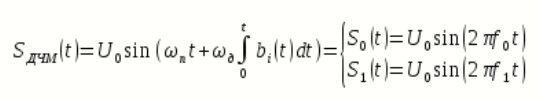
Разложение сигнала по гармоническим составляющим имеет следующий вид:





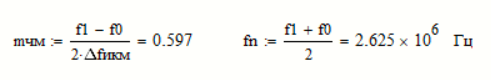
При не известной амплитуде 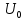вычисляют нормированный спектр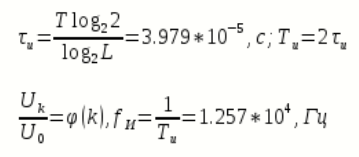



Ширина спектра сигнала ДЧМ равна:



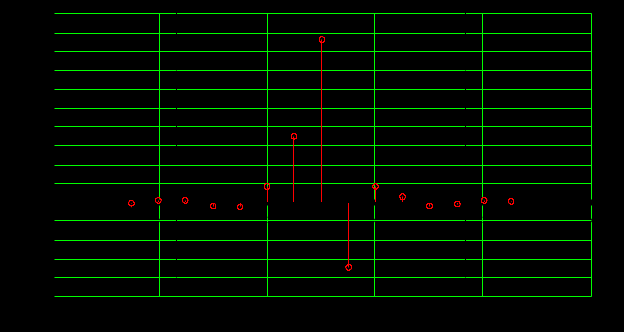
б) построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра

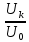
График нормированного спектра сигнала дискретной модуляции.

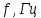
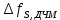
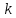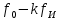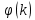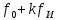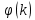0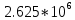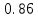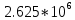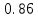
1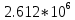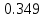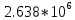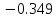
2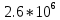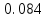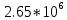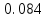
3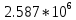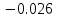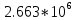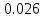
4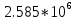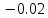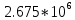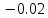
5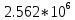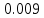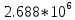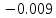
6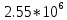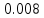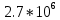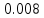
7

7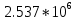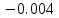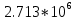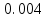. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:

а) рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС;

Мощность гауссовского белого шума 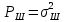в полосе пропускания ПФ геометрически определяется как площадь прямоугольника с высотой 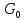и основанием :



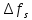Учитывая, что начальное соотношение сигнал-шум(ОСШ)

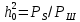на входе детектора приемника известно, находим мощность сигнала дискретной модуляции, обеспечивающей это ОСШ:



Рассчитаем приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала:



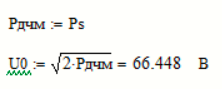
Пропускная способность НКС характеризует максимально возможную скорость передачи информации по данному каналу. Она определяется:



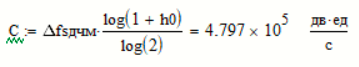
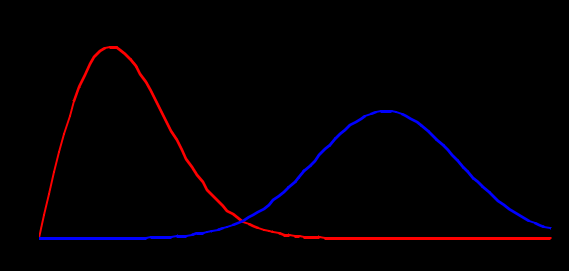
б) построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП.

ФПВ мгновенных значений УГП имеют вид гауссовского распределения с числовыми характеристиками 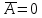— математическое ожидание,

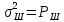— мощность.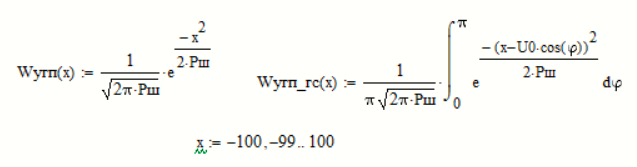






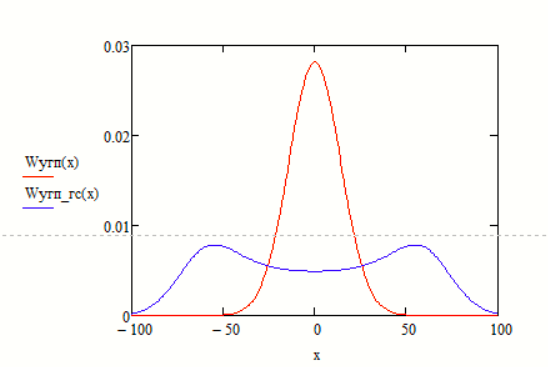
Огибающая гауссовской помехи распределена по закону Рэлея:



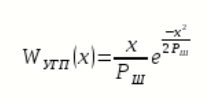
Огибающая принимаемой суммы гармонического сигнала + УГП подчиняется обобщенному распределению Рэлея:



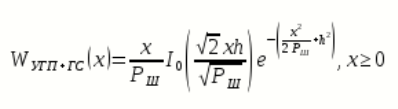
Где 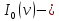модифицированная функция Бесселя нулевого порядка от мнимого аргумента

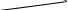
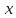
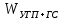
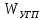
8. С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:

а) рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС;
За количественную меру помехоустойчивости в системах электросвязи принимают среднюю на бит вероятность ошибки:



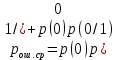
При равенствах априорных вероятностей 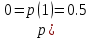, а так же условных вероятностей 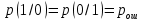(условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна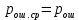


Скорость передачи информации по двоичному симметричному ДКС, когда 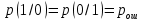определяется: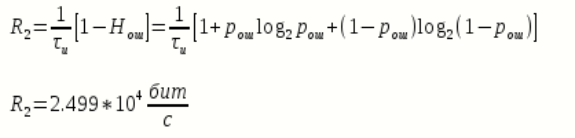



Т.к. вероятность ошибок 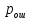для различных видов сигналов зависят от 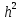на входе детектора, то и 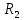зависит от ОСШ. Для сравнения скорости 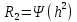при данном виде модуляции и способе приема с пропускной способностью НКС 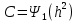вводят показатель эффективности



б) изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи, когда он выносит ошибочные решения.
Приемник сигналов ДЧМ



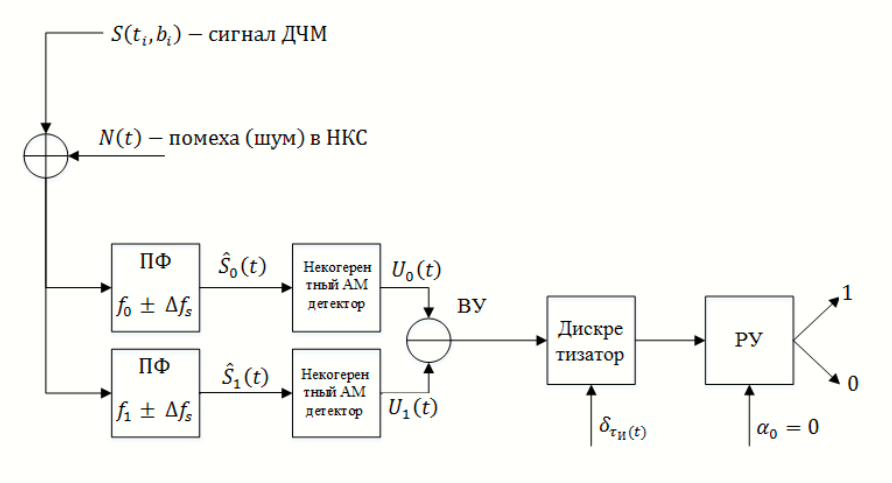
Детектор, представляющий собой линейную систему с переменными параметрами, схема детектора состоит из перемножителя и ФНЧ, прошедшего полосовой фильтр с эффективной полосой пропускания равной 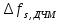к детектору подводятся опорный сигнал 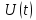и перемножается с принятым, после чего оба перемноженных сигнала поступают на вычитающее устройство, далее сигнал поступает на дисретизатор к которому подводится последовательность дискретизирующих импульсов 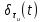с периодом 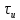, которые необходимы для взятия отсчета в середине посылки длительностью 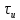. В РУ (решающем устройстве) отсчеты 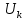сравниваются с пороговым напряжением 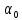и принимается решение - передана 1, если 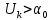, или передан 0, если 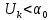. Под действием помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0.

9. Рассматривая отклик детектора ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС:

а) рассчитать распределение вероятностей дискретного сигнала на выходе детектора, скорость передачи информации по L- ичному ДКС, относительные потери в скорости передачи информации по L- ичному ДКС;

Распределение вероятностей дискретного сигнала на выходе детектора определяется выражением:

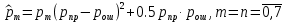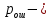, где вероятность ошибки в двоичном симметричном ДКС; 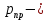вероятность правильного приема двоичного символа,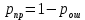

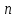	0	1	2	3	4	5	6	7
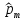	0.0017	0.022	0.136	0.341	0.341	0.136	0.022	0.0017

Для определения скорости передачи информации 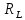по L — ичному ДКС

воспользуемся соотношением:



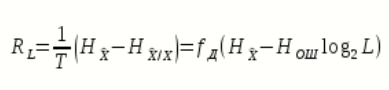
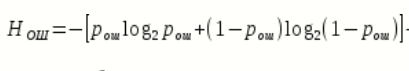
Где 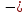энтропия ошибочных решений



Зная производительность 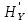L — ичного источника(скорость ввода информации в ДКС) и скорость передаваемой по ДКС информации 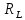находим величину относительных потерь в скорости:



б) построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя.

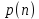
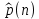
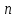
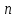
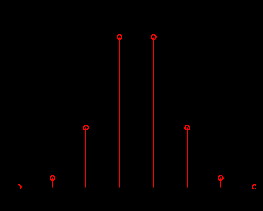
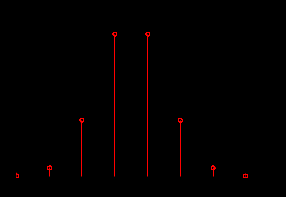
10. Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:

а) рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шумапередачи (СКПП) суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП);

Дисперсия случайных импульсов шума передачи на выходе интерполятора ЦАП определяется:



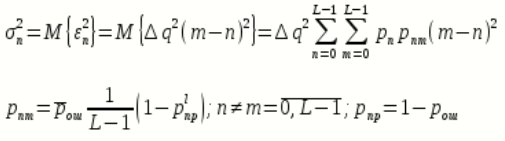
Где 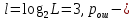вероятность ошибки в двоичном симметричном ДКС.

Найдем СКПП:



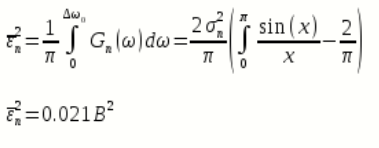
В виду того, что погрешность фильтрации 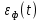шум квантования 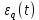и шум передачи 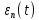- независимые случайные процессы, то суммарная СКП восстановления непрерывного сообщения 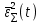будет равна сумме СКП указанных процессов: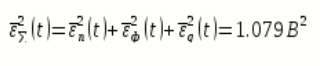



Тогда относительная суммарная СКП восстановленного сообщения, очевидно будет равна:

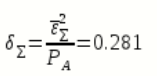
11. В виду того, что выбор начальной энергетической ширины спектра исходного сообщения не приводит к минимуму ОСКП, решить оптимизационную задачу: с помощью ЭВМ определить оптимальную энергетическую ширину спектра сообщения, доставляющую минимум относительной суммарной СКП его восстановления.

Относительная суммарная СКП восстановления сообщения равна:



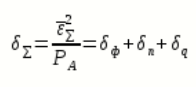
Не трудно показать, что относительные СКП фильтрации 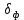, квантования 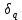и передачи 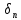зависят от энергетической ширины спектра сообщения 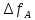различным образом: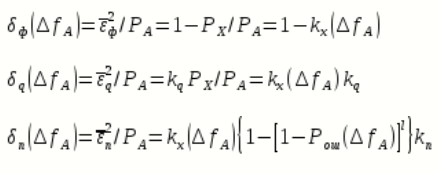



Где ;



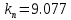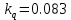
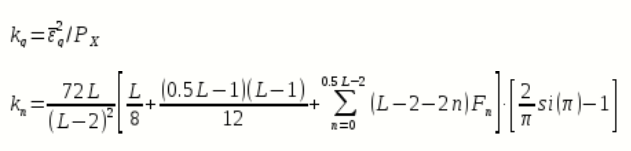
Где 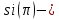интегральный синус: 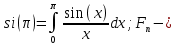интегральный закон распределения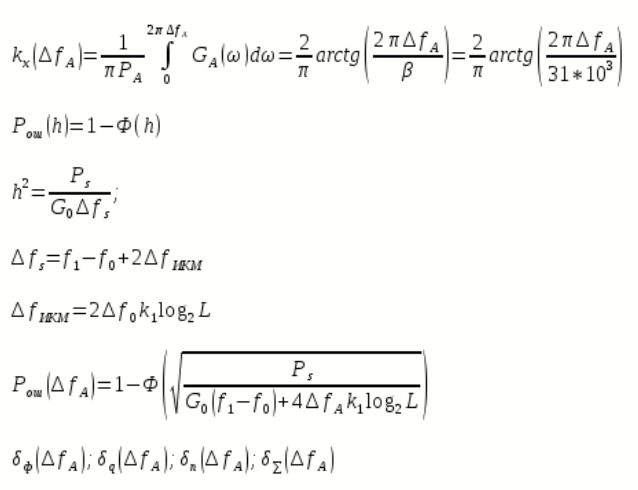













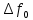
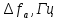
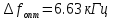
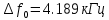
Суммарная величина относительной СКП имеет минимум при оптимально выбранной энергетической ширине спектра исходного сообщения.

Список использованной литературы.

1. 
   В.Г. Санников - Методические рекомендации по выполнению курсовой работы-М.:1996.
   
2. 
   А.Г. Зюкл, Д.Д. Кловский. ТЭС: Учебник для вузов - М.:Радио и связьБ 1998г.
   
3. 
   Конспект лекцийй