ВУЗ: Кемеровский государственный университет культуры и искусств
Категория: Лекция
Дисциплина: Статистика
Добавлен: 06.02.2019
Просмотров: 443
Скачиваний: 7
Тема 3.1. ВЫБОРОЧНЫЙ МЕТОД
План лекции:
-
Выборка
-
Статистическое распределение выборки
-
Графическое изображение вариационных рядов
-
Эмпирическая функция распределения
Список литературы:
-
Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.
-
Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. - М.: Высшая школа, 2007. - 480 с.
-
Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер - М: ЮНИТИ, 2002. – 543 с.
п.1 Выборка
Математическая статистика – это наука, занимающаяся разработкой методов сбора, регистрации и обработки результатов наблюдений (измерений) с целью познания закономерностей случайных массовых явлений.
Результаты измерений (наблюдений) называют статистическими данными.
Одним из основных способов сбора статистических данных является выборочный метод.
Во многих практических задачах, связанных с повторяющимися испытаниями, нельзя провести все возможные испытания, а можно проделать лишь доступную, выборочную их часть, а затем сделать обоснованный вывод. Например, условимся считать некоторый ноутбук стандартным, если продолжительность его работы составляет 5000 часов, в противном случае он считается нестандартным. Исследовать каждый ноутбук на продолжительность работы невозможно. Тогда как получить представление о качестве изготавливаемых ноутбуков? Для этого достаточно иметь сведения о качестве небольшого числа ноутбуков, отобранных случайно. Тогда по продолжительности работы отобранных приборов можно судить о качестве всей партии.
Совокупность всех возможных значений, или реализаций, исследуемых случайных величин называется генеральной совокупностью. Она может состоять из конечного или бесконечного множества значений, называемых элементами генеральной совокупности.
Выборочной совокупностью (или просто выборкой) называется совокупность элементов случайно отобранных из генеральной совокупности.
Объемом совокупности (генеральной или выборочной) называют число элементов этой совокупности.
Метод, основанный на том, что по данным обследования выборки, выделенной из генеральной совокупности, делается заключение о всей генеральной совокупности, называется выборочным методом.
Задача математической статистики состоит в исследовании свойств выборки и обобщении этих свойств на всю генеральную совокупность. Полученный при этом вывод называется статистическим.
Основное требование к выборке: она должна хорошо представлять генеральную совокупность, т.е. быть репрезентативной (представительной). Выборка будет репрезентативной, если её осуществлять случайным образом.
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяются на повторные и бесповторные.
Повторной называют выборку, при которой отобранный элемент (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный элемент в генеральную совокупность не возвращается.
На практике чаще используется бесповторная выборка.
Кроме того, различают следующие способы составления выборки: а) простой (случайный), б) механический, в) типический, г) серийный.
Так, если занумеровать все элементы генеральной совокупности и затем изготовить карточки с такими же номерами, тщательно перемешать их и отобрать пачку карточек, то элементы генеральной совокупности с номерами извлечённых карточек образуют простую (случайную) выборку. Здесь возможно повторная и бесповторная выборка.
Если элементы генеральной совокупности выбираются через определённый интервал, то такая выборка называется механической. Например, при анализе качества ноутбуков, сходящих с конвейера, отбирается каждый 25 ноутбук.
Предположим теперь, что генеральную совокупность разбили на несколько неперекрывающихся групп и из каждой группы отобраны в случайном порядке объекты. Это типический способ (районированная или стратифицированная выборка) составления выборки. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, при определении рейтинга кандидатов в президенты на выборах страну делят на округа и в каждом округе определяется рейтинг кандидатов в президенты.
Наконец, серийная (гнездовая или кластерная) выборка образуется следующим образом. Генеральная совокупность делится на неперекрывающиеся группы. После этого случайным образом отбираются некоторые группы. Полученная выборка будет серийной.
На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
Разумеется, если бы мы могли провести сплошное обследование всех элементов генеральной совокупности, то не нужно было бы применять никакие статистические методы, и саму математическую статистику можно было бы отнести к чисто теоретическим наукам. Однако такой полный контроль невозможен по следующим причинам. Во-первых, часто испытание сопровождается разрушением испытуемого объекта; в этом случае мы имеем выборку без повторения. Во-вторых, обычно необходимо исследовать весьма большое количество объектов, что просто невозможно физически, и т.д.
п.2 Статистическое распределение выборки
Как правило, результаты эксперимента или наблюдения дискретных случайных величин (первичные данные) сводятся в таблицу, в первой строке которой записывается номер i эксперимента, а во второй – соответствующий признак xi, называемый вариантой случайной величины. Таблицы такого вида называются статистическими рядами несгруппированных данных. Таблица может включать данные о нескольких признаках (несколько видов вариант), но часто ограничиваются данными об одном признаке.
Статистический ряд несгруппированных данных не позволяет проводить содержательный анализ. Учитывая, что нередко статистические исследования охватывают совокупность численностью десятки и сотни тысяч объектов, возникает необходимость упорядочения первичных данных. Для этого используются статистические методы ранжирования и группировки. Иногда этих приёмов обработки статистических данных достаточно для последующего анализа. Чаще приходится прибегать к более сложным методам, но и тогда предварительное упорядочение является обязательной операцией.
Ранжированием называется расположение элементов совокупности в порядке возрастания или убывания величины соответствующих им вариантов.
Статистический ряд, расположенный по возрастанию вариант, называется вариационным рядом.
Ранжированный перечень содержит список элементов совокупности упорядоченный по возрастанию. Каждому элементу (и соответствующему ему варианту) приписан ранг – номер занимаемого им места. Одинаковые варианты получают одинаковый ранг.
После ранжирования данных легко заметить, что некоторые варианты повторяются несколько раз. Если представить совокупность в виде таблицы , в которой записано сколько раз встречаются совокупности с одинаковой вариантой, она станет ещё более обозримой и удобной для анализа по сравнению с ранжированным рядом. Этот приём называется дискретной группировкой.
Дискретной группировкой называется распределение совокупности вариантов по группам, содержащим одинаковые варианты.
Число, показывающее сколько раз (как часто) некоторый вариант xi встречается в совокупности, называется частотой ni (абсолютной частотой) данного варианта. Сумма всех частот равняется количеству элементов совокупности (объему выборки), т.е.
![]() .
(1)
.
(1)
Относительной
частотой
(частостью)
![]() некоторого варианта xi
называется доля этого варианта в общем
количестве данных, т.е. отношение частоты
к объему выборки:
некоторого варианта xi
называется доля этого варианта в общем
количестве данных, т.е. отношение частоты
к объему выборки:
![]() .
(2)
.
(2)
Для удобства относительную частоту часто выражают в процентах, умножая результат на 100.
Соответствие между вариантами и их частотами (относительными частотами) называется статистическим распределением выборки.
Одновременно с понятием частоты и относительной частоты в сгруппированных совокупностях применяются понятия накопленной частоты и относительной частоты.
Накопленной
частотой
![]() некоторого варианта xi
называется количество элементов
ранжированной в порядке возрастания
совокупности, имеющих значение признака
меньше или равное данному:
некоторого варианта xi
называется количество элементов
ранжированной в порядке возрастания
совокупности, имеющих значение признака
меньше или равное данному:
![]() .
(3)
.
(3)
Накопленной
относительной частотой
![]() некоторого варианта xi
называется отношение накопленной
частоты этого варианта
некоторого варианта xi
называется отношение накопленной
частоты этого варианта
![]() к объему выборки:
к объему выборки:
![]() .
(4)
.
(4)
В тех случаях, когда число различных вариантов в совокупности велико или вариация является непрерывной при обработке статистических данных используется интервальная группировка.
Интервальной группировкой называется распределение совокупности вариантов на группы вариантов, лежащих в определённых границах.
Статистическая таблица, получаемая в результате интервальной группировки, называется интервальным вариационным рядом.
Максимальное значение варианта для конкретного интервала называется верхней границей xi(max), а минимальное – нижней границей интервала xi(min). Величина интервала – разность между верхней и нижней границами интервала:
![]() .
(5)
.
(5)
Понятия частоты, относительной частоты, накопленной частоты и накопленной относительной частоты интервального вариационного ряда аналогичны соответствующим понятиям дискретного вариационного ряда, но относятся не к отдельному признаку. А ко всему интервалу.
Ещё одним способом группировки совокупности является комбинационная группировка – распределение совокупности на группы по сочетанию (комбинации) нескольких признаков.
п. 4 Графическое изображение вариационных рядов
Для наглядности рассмотрения статистических данных ряды распределения представляются в графической форме. Наиболее широко используются следующие виды графического изображения вариационных рядов в прямоугольной системе координат: полигон, гистограмма, кумулятивная кривая.
Эти графики дают возможность представить характер варьирования значений признака, выявить состав изучаемой совокупности, её структуру и структурные сдвиги. При нанесении на единую координатную сетку, возможно сравнение нескольких вариационных рядов.
Полигоном (многоугольником) распределения называется графическое изображение вариационного ряда в прямоугольной системе координат, при котором величины признака (варианты) xi откладываются на оси абсцисс, а частоты (или относительные частоты) на оси ординат.
Таким образом, полигон частот представляет собой ломанную, отрезки которой соединяют точки M1(x1, n1), M2(x2, n2), …, Mk(xk, nk). Полигон относительных частот есть ломанная, отрезки которой соединяют точки M1(x1, ω1), M2(x2, ω 2), …, Mk(xk, ω k). Крайние точки М1 и М2, если они не лежат на оси абсцисс, обычно также соединяют со смежными точками M0(x0, 0), Mk+1(xk+1, 0).
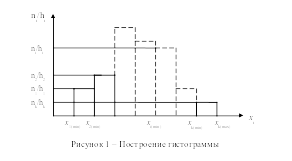
Гистограммой вариационного ряда называется графическое изображение интервального вариационного ряда в виде прямоугольников, основания которых – отрезки оси абсцисс, соответствующие интервалам изменения признака, а высоты пропорциональны плотностям частот (или относительных частот) интервалов.
В случае непрерывных
интервалов гистограмма частот строится
следующим образом (см. Рисунок 1): на оси
абсцисс наносится шкала для интервалов,
на оси ординат – для плотностей частот
интервалов
![]() .
Из всех точек на оси абсцисс восстанавливаются
перпендикуляры, на которых последовательно,
начиная с первого, откладываются значения
плотности частот интервалов.
.
Из всех точек на оси абсцисс восстанавливаются
перпендикуляры, на которых последовательно,
начиная с первого, откладываются значения
плотности частот интервалов.
Кумулятивная кривая (кумулята) это графическое изображение вариационного ряда, составленное по последовательно суммированным, т.е. накопленным частотам (или относительным частотам).
При построении кумулятивной кривой дискретного вариационного ряда на ось абсцисс наносят значения варианты, ординатами служат нарастающие итоги частот (или относительных частот). Ломаная линия, соединяющая вершины ординат образует кумулятивную кривую.
п. 3 Эмпирическая функция распределения
Пусть известно статистическое распределение частот случайной величины X.
Эмпирической
функцией распределения (или функцией
распределения выборки) называется
функция
![]() ,
определяющая для каждого значения x
относительную частоту события X<x:
,
определяющая для каждого значения x
относительную частоту события X<x:
![]() ,
(6)
,
(6)
где nx – число вариант, меньших x; n – объем выборки.
Таким образом, для
того чтобы найти, например,
![]() ,
надо число вариант, меньших x2,
разделить на объем выборки:
,
надо число вариант, меньших x2,
разделить на объем выборки:
![]() .
.
Из определения
эмпирической функции следует, что
![]() обладает всеми свойствами функции
распределения F(x),
а именно:
обладает всеми свойствами функции
распределения F(x),
а именно:
-
значения функции
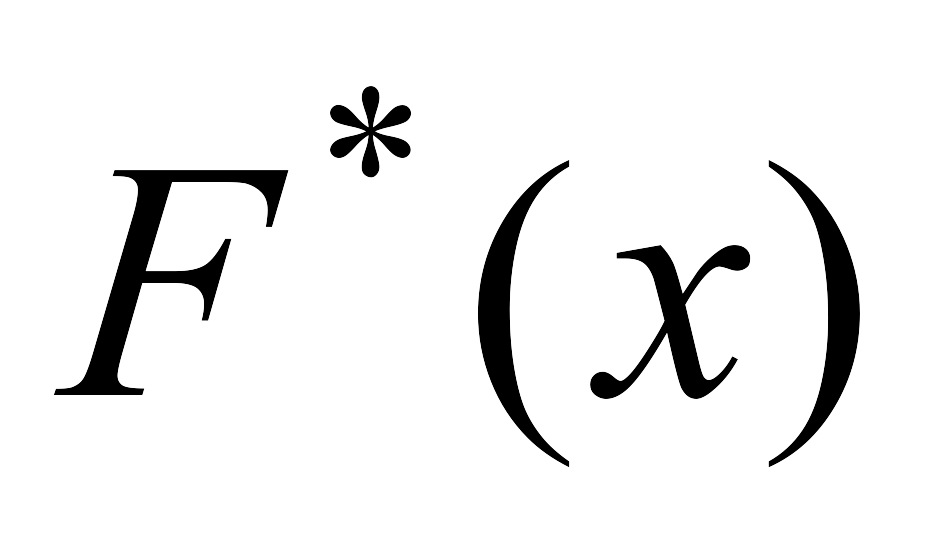 принадлежат интервалу [0,1];
принадлежат интервалу [0,1]; -
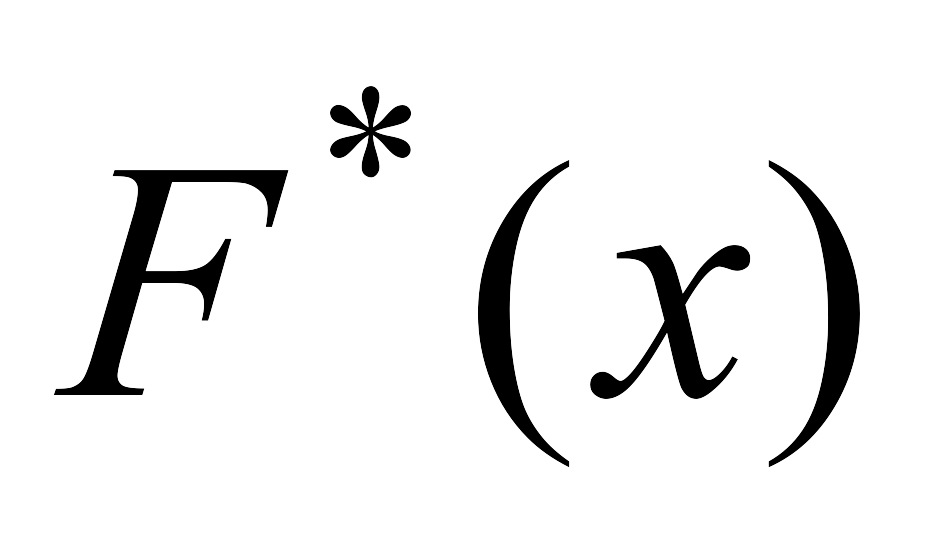 - неубывающая
функция;
- неубывающая
функция; -
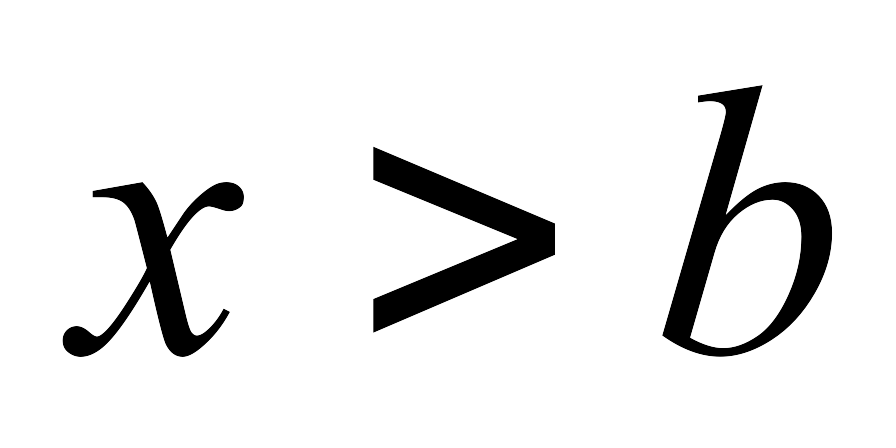
если а – наименьшая, а b – наибольшая варианта, то
 при
при
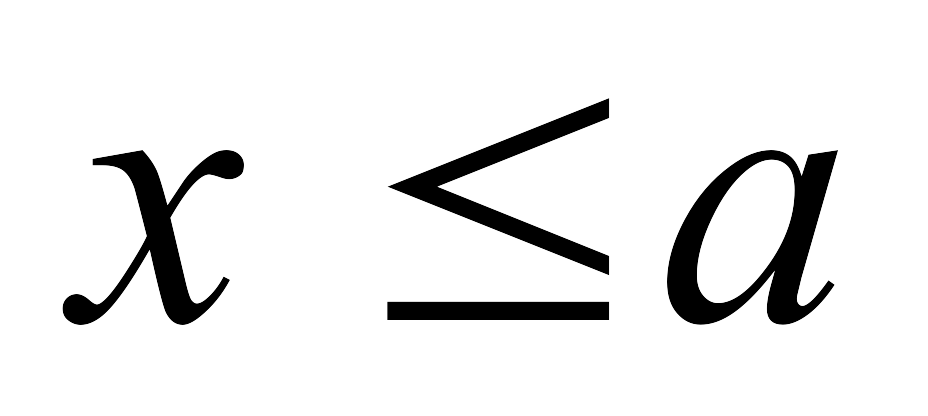 и
и
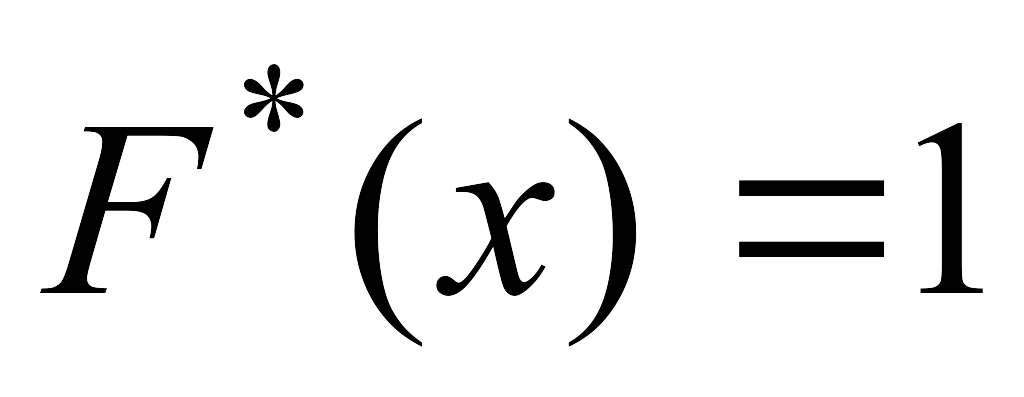 при
при
 .
.
Функцию распределения
![]() ,
в отличие от эмпирической функции
,
в отличие от эмпирической функции![]() ,
называют теоретической функцией
распределения. Различие между эмпирической
и теоретической функцией распределения
состоит в том, что первая определяет
относительную частоту события X<x,
а вторая – вероятность того же события.
,
называют теоретической функцией
распределения. Различие между эмпирической
и теоретической функцией распределения
состоит в том, что первая определяет
относительную частоту события X<x,
а вторая – вероятность того же события.
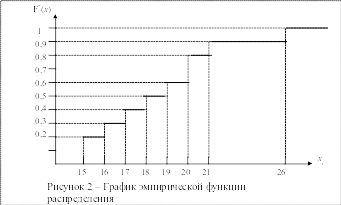
Построим эмпирическую
функцию распределения. Из свойств
функции
![]() и данных таблицы получаем:
и данных таблицы получаем:
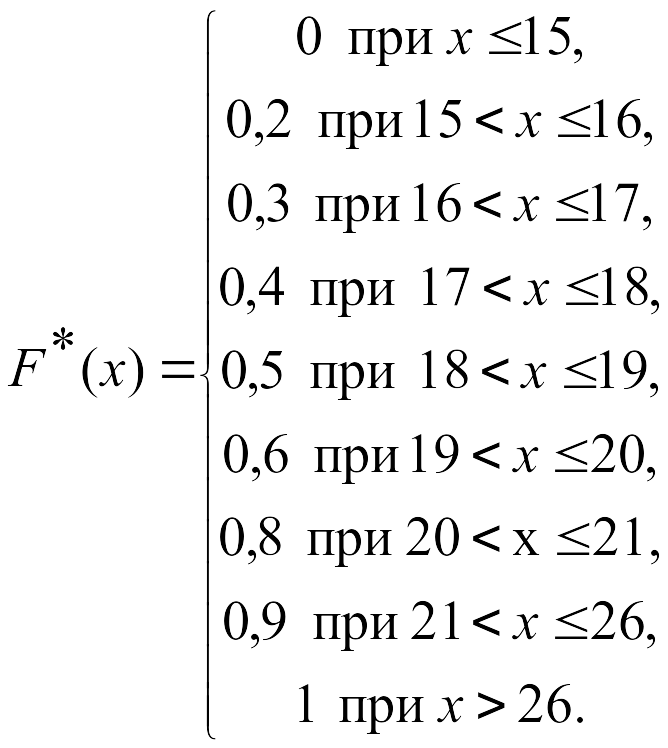
График функции
![]() изображён на рисунке 2.
изображён на рисунке 2.