Файл: Отчет по лабораторной работе по дисциплине Вычисления в инфокоммуникациях.docx
Добавлен: 07.12.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ Государственное АВТОНОМНОЕ образовательное УЧРЕЖДЕНИЕ ВЫСШЕГО образования
БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
(НИУ «БелГУ»)
ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ
Отчет по лабораторной работе
по дисциплине: «Вычисления в инфокоммуникациях»
Лабораторная работа №1. «Метод Гаусса решения системы линейных алгебраических уравнений и его модификации»
Студента заочного отделения
2 курса 12002153 группы
Пасивенко А.Ю.
Проверил:
Балабанова Татьяна Николаевна
Белгород 2023
Цель работы:
Освоить реализацию алгоритмов решения систем линейных алгебраических уравнений по методу Гаусса.
1. Задание: Реализовать метод Гаусса решения системы линейных алгебраических уравнений.
Данные:
| | 6 | 9 | 9 | 7 | 9 |
| | 8 | 4 | 9 | 2 | 5 |
| | 5 | 5 | 2 | 3 | 2 |
| | 3 | 1 | 4 | 4 | 4 |
Решение:
Необходимо поэтапно приводить систему к треугольному виду исключая из последовательно сначала
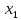из первого, второго, n-го уравнения, 
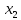из третьего, четвёртого, n-го уравнения и т.д. Все уравнения заменяются на полученные из сложенные с первым, умноженным на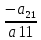 
,
… 
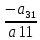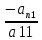, получится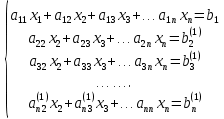
Где коэффициенты считаются
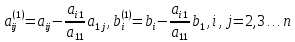
На втором этапе производятся те же операции, что и на первом, с получившейся матрицей, но с
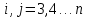. Продолжая процесс, матрица приходит к треугольному виду, этот этап называется прямым ходом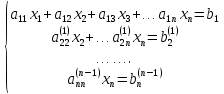
Такая матрица позволяет вычислять все элементы, начиная с последнего, этот этап называется обратным ходом, который определяется формулой
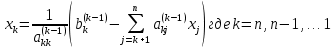
На основании этого была построена блок-схема алгоритма решения
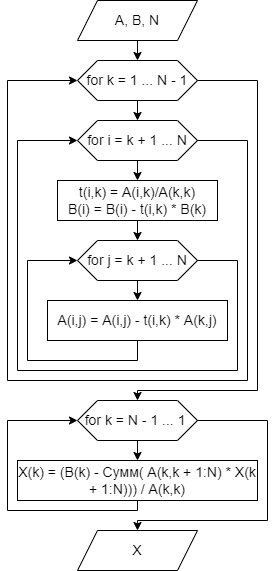
Рисунок 1 – Блок-схема программы решения СЛАУ методом Гаусса
Листинг программы
clear,clc;
A = [6,9,9,7; 8,4,9,2; 5,5,2,3; 3,1,4,4]; %коэффициенты
B = [9; 5; 2; 4]; %значения
N = 4; %число уравнений
A1 = [A B];
for k=1:1:N-1
for i=k+1:1:N
t(i,k) = A(i,k) / A(k,k);
B(i) = B(i) - t(i,k) * B(k);
for j=k+1:1:N
A(i,j) = A(i,j) - t(i,k) * A(k,j);
end
end
end
X(N) = B(N) / A(N,N);
for k=N-1:-1:1
X(k) = (B(k) - sum(A(k,k+1:N).*X(k+1:N)))/A(k,k);
end
X’
Вывод:__2._Задание'>Вывод:
2. Задание: Реализовать метод Гаусса с постолбцовым выбором главного элемента.
Данные.
| | 6 | 9 | 9 | 7 | 9 |
| | 8 | 4 | 9 | 2 | 5 |
| | 5 | 5 | 2 | 3 | 2 |
| | 3 | 1 | 4 | 4 | 4 |
Решение:
Для того чтобы уменьшить влияние ошибок округлений и исключить деление на 0, на каждом этапе прямого хода уравнения системы представляют так, чтобы деление производилось на максимальный элемент по модулю в данном столбце. Для этого необходимо модифицировать алгоритм из первого задания, добавив между вторым и третьим элементом блок-схемы поиск
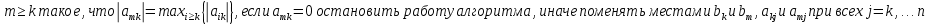
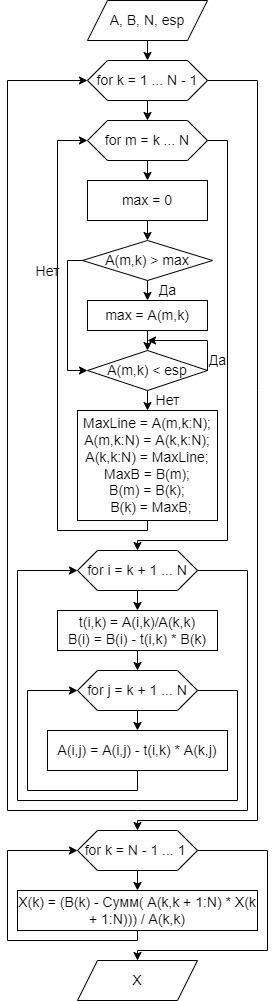
Рисунок 2 – Блок-схема программы решения СЛАУ методом Гаусса с постолбцовым выбором главного элемента
Листинг программы
clear, clc
A = [6,9,9,7; 8,4,9,2; 5,5,2,3; 3,1,4,4]; %коэффициенты
B = [9; 5; 2; 4]; %значения
N = 4; %число уравнений
esp = 0.001; %точность
for k=1:1:N-1
for m=k:1:N
max = 0;
if abs(A(m,k)) > max
max = abs(A(m,k));
end
if A(m,k) < esp continue;
else MaxLine = A(m,k:N);
A(m,k:N) = A(k,k:N);
A(k,k:N) = MaxLine;
MaxB = B(m);
B(m) = B(k);
B(k) = MaxB;
end
end
for i=k+1:1:N
t(i,k) = A(i,k) / A(k,k);
B(i) = B(i) - t(i,k) * B(k);
for j=k+1:1:N
A(i,j) = A(i,j) - t(i,k) * A(k,j);
end
end
end
X(N) = B(N) / A(N,N);
for k=N-1:-1:1
X(k) = (B(k) - sum(A(k,k+1:N).*X(k+1:N)))/A(k,k);
end
X’
Вывод:
Вывод: Был изучен и реализовал метод Гаусса решения СЛАУ, а также его модификация — решение с постолбцовым выбором главного элемента. Сущность методов заключается в прямой обработке матрицы и обратной подстановке по строкам, но в методе главных элементов для большей точности при каждой итерации строка с максимальным элементом переставляется наверх и пропускаются элементы меньшие необходимого значения точности.