Файл: Практическая работа 13. Координаты вектора. Решение задач на определение координат вектора.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 58
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа №13. Координаты вектора. Решение задач на определение координат вектора
Рассмотрим координатную плоскость и в ней единичные векторы i и j, которые сонаправлены осям координат, и длина которых равна единичному отрезку:
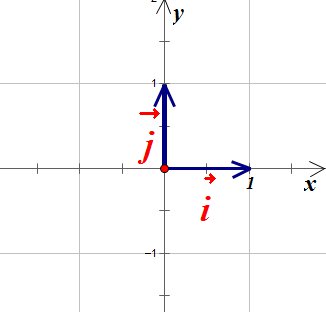
Эти векторы называются базисными. Тогда любой вектор мы можем представить в виде линейной комбинации базисных векторов:
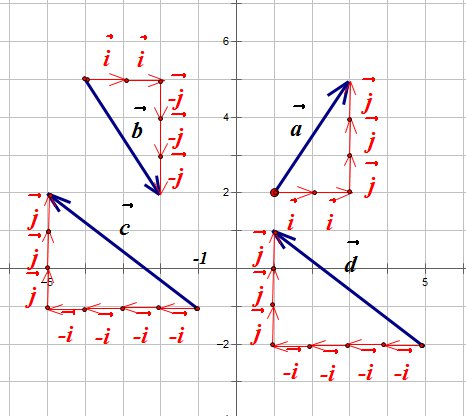
Мы видим, что
Для произвольного вектора
числа 
и 
в разложении вектора 
по базисным векторам называются координатами вектора.
Координаты векторов на рисунке выше:
Внимание! При записи координат вектора мы всегда на первом месте пишем коэффициент при i, а на втором месте коэффициент при j.
Два вектора равны
, если они имеют одинаковую длину и сонаправлены. Два равных вектора имеют одинаковые координаты. Мы видим, что
Если начало вектора совпадает с началом координат, то координаты вектора совпадают с координатами его конца:
и 
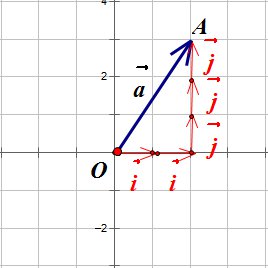
Если вектор
задан координатами его начала 
и конца 
, то чтобы найти его координаты, нужно из координат конца вектора вычесть координаты начала:
Два вектора называются противоположными, если они имеют одинаковую длину, лежат на параллельных прямых и направлены в противоположные стороны:
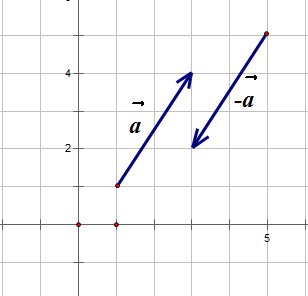
Противоположные векторы имеют противоположные координаты:
При умножении вектора на число все координаты вектора умножаются на это число:
Если
, то 
Если число k>0, то векторы
и
сонаправлены.Если число k<0, то векторы
и направлены в противоположные стороны.Вектора, которые лежат на параллельных прямых, называются коллинеарными.
Если вектора
и 
коллинеарны, то их координаты пропорциональны: 
При вычитании векторов их координаты вычитаются:
Если
, и 
, то 
При сложении векторов их координаты складываются:
Если
, , и 
, то 
Пример.
, 
. Найдите координаты вектора 
;
Длина вектора
вычисляется по формуле: 
Если вектор
задан координатами его начала 
и конца 
, то его длина вычисляется по формуле:
С помощью этой же формулы находится длина отрезка
, или расстояние между точками 
и 
.Если точка
является серединой отрезка , то ее координаты вычисляются по формуле: 
Скалярным произведением векторов
и 
называется число, равное произведению длин векторов на косинус угла между ними:
Скалярное произведение векторов
и 
равно сумме произведений одноименных координат.
Если мы приравняем правые части выражений для скалярного произведения, мы получим формулу для нахождения косинуса угла
между векторами и :
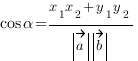
Выразим длины векторов через их координаты и получим формулу, выражающую косинус угла между векторами через координаты векторов:
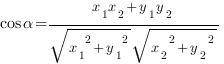
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
Пример 1 . Вектор
с началом в точке A(3; 6) имеет координаты (9; 3). Найдите сумму координат точки B.
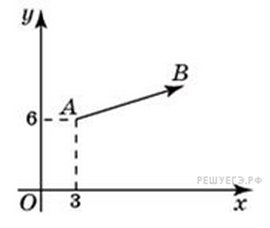Пусть координаты точки 
. Тогда 
Отсюда:
, значит, 
, значит, 