Файл: Основные представления нелинейной динамики.docx

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра МИТ


РЕФЕРАТ

Дисциплина: Физические Основы

Микро- и Наноэлектроники

Тема:

«Основные представления нелинейной динамики»

Студент гр. 1111		Федоров С.И.
Руководитель		Рассадина А.А.

Санкт-Петербург

2022

Содержание

Аннотация

Нелинейная динамика, предметом исследований которой является анализ сложных эволюционных процессов в принципиально нелинейных системах, сформировалась в качестве научного направления сравнительно недавно, примерно за последние 25-30 лет. Пока не создано четкой программы, тем более стандарта этой дисциплины, которая продолжает интенсивно развиваться.

Кратко невозможно описать предмет изучения нелинейной динамики, однако на базе даже одного примера можно полноценно проиллюстрировать важность данного ответвления в науке.

Когда мы рассматриваем электрическую цепь на начальном этапе обучения базовой электротехнике и находим по закону Ома необходимые величины (ток, напряжение или сопротивление), мы берем очень условно каждый из этих элементов, очень тривиально. Если углубляться и рассматривать цепь более сложную, содержащую C- или L-элемент, можно обнаружить, что цепь приобрела динамические свойства. Реакцию цепи n-го порядка можно найти как 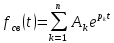, где 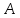– постоянный коэффициент, 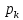– частоты собственных колебаний, которые являются корнем характеристического уравнения, получаемого из однородного дифференциального уравнения заменой

---

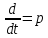. Иными словами, некоторые величины нельзя описать с помощью линейных законов сложения и умножения, необходимы более детальные и индивидуальные подходы к решению данных задач.

Введение

Цель: целью данной научной работы является изучение основных представлений нелинейной динамики и использование ее методов в прикладных науках. Нелинейная динамика является одним из основных методов в исследовании в прикладных науках, таких как радиотехника (анализ сигналов), электротехника (анализ свободных и вынужденных состояний цепей), прикладная механика (анализ маятников) и др. Бо́льшая часть нелинейной динамики вытекает из математического анализа и математической статистики. Без изучения в области нелинейной динамики невозможно было бы дать оценку некоторым физическим величинам, ведь их описание с помощью линейных (или же коммутативных) способов дает ложные результаты.

Задачи:

• 
  Дать определение нелинейной динамики и ее отличий от линейной;
  
• 
  Рассмотреть динамические системы как метод нелинейной динамики;
  
• 
  Рассмотреть переход от детерминированности к хаосу с точки зрения нелинейной динамики.
  

Определение нелинейной динамики [2]

Нелинейная динамика – раздел современной математики, занимающийся исследованием нелинейных динамических систем.

Под динамической системой условились понимать систему любой природы (физическую, химическую, биологическую, социальную, экономическую и др.), состояние которой изменяется (дискретно или непрерывно) во времени. Также основным свойством динамической системы является возможность изучаемым предсказать дальнейший ход системы с помощью математических преобразований.

Нелинейная динамика использует при изучении нелинейные модели – дифференциальные уравнения и дискретные отображения.

Следует отметить, что дать точное определение предмета изучения нелинейной динамики довольно сложно, однако, как подчеркнул один из основоположников теории колебаний и нелинейной динамики Л.И. Мандельштам, что в методе колебаний важно не дать точное понятие чем занимается этот раздел науки, но важно определить и выделить руководящие идеи и основные общие закономерности. Эту цитату можно проецировать и на понятие нелинейной динамики.

---

Одним из важных отличий нелинейной динамики от линейной является отсутствие возможности применения метода суперпозиции.

Изучение линейной динамики учеными привело их в настоящий тупик, так как, пытаясь анализировать физические процессы с его помощью, натыкались на противоречия между теорией и практикой в исследованиях. В метолах линейной динамики теория была идеализирована и понятна с помощью линейного математического аппарата. Русский ученый-физик Л.И. Мандельштам писал, что искусственная линеаризация процессов оказывалась малоэффективной, большей частью ничему не научала, а иногда бывала прямо вредной.

Однако полный отказ от принципа суперпозиции не произошел, так как, во-первых, он был полностью изучен учеными, а во-вторых, все еще остались процессы, которые с практической и философской точки зрения оставались тривиальными и описание их с помощью линейной физики оставалось верным.

Разобравшись с разницей между линейной и нелинейной динамикой, можно приступить к изучению основных методов и понятий в нелинейной динамике.

Динамические системы как метод нелинейной динамики [3]

Динамическая система была формально определена, если заданы три следующих элемента:

1. 
   Множество состояний Х, образующее полное метрическое пространство (фазовое пространство);
   
2. 
   Множество моментов времени ;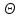
   
3. 
   Оператор эволюции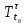 – некоторое отображение 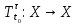, которое каждому состоянию 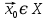в начальный момент времени 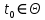однозначно ставит в соответствие некоторое состояние 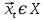в любой другой момент времени 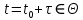. Таким образом, можно записать:
   

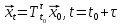(1)

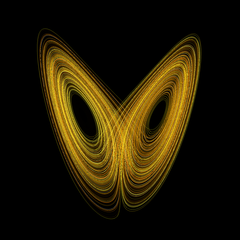
Рис. 1. Фазовая диаграмма странного аттрактора Лоренца — популярный пример нелинейной динамической системы.

---

Оператор эволюции является непрерывным в X и обладает следующими свойствами:

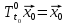	(2)
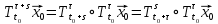	(3)

Где 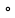означает суперпозицию операторов.

Исходя из характера множеств 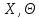и свойств оператора эволюции можно дать наиболее общую классификацию динамических систем.

Исходя из характера множеств Х, и свойств оператора эволюции можно дать наиболее общую классификацию динамических систем. Если 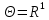, то есть время принимает непрерывное множество значений, то оператор эволюции непрерывен по 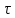и соответствующую динамическую систему называют системой с непрерывным временем или потоком, по аналогии с течением жидкости. Если множество является счетным, то динамическую систему называют системой с дискретным временем или каскадом.

Если оператор эволюции сохраняет фазовый объем, то динамическая система называется консервативной. Полная энергия консервативной системы остается постоянной. Если оператор эволюции сжимает фазовый объем, то система называется диссипативной. В такой системе происходит рассеяние (диссипация) энергии.

Нейронные сети [4]

Вычислительные машины дали очень много нелинейной динамике. Они позволили исследовать математические модели, возникающие в разных областях, и обнаружить множество интересных нелинейных эффектов.

Компьютерное моделирование играет важную роль в междисциплинарном подходе, называемом нейронаукой. Этот подход призван ответить на вопрос, как работает мозг, какие психические события определяются паттернами нервных импульсов в мозге.

Развитие нейронауки показало, что основным способом понимания протекающих в мозге процессов, осмысление имеющихся экспериментальных данных, постановки новых проблем является построение и исследование математических моделей. Модели скорее отвечают на вопрос, как могли бы работать те или иные системы, в каких-то чертах согласующиеся с данными об архитектуре, функциях, особенностях мозга. Тем не менее исследования в нейронауке уже открыли пути для создания новых компьютерных архитектур и наделению памяти наделению вычислительных систем своеобразной интуицией, ассоциативной памятью, способностью к обучению и обобщению поступающей информации, т.е. возможностями, которые раньше считались прерогативами живых систем.

---

Огромный интерес, проявляемый к этим работам в последние пятнадцать лет, обусловлен несколькими причинами. В 60-е и 70-е годы большие надежды возлагались на научное направление, называемое искусственным интеллектом. Предполагалось, что, опираясь на логику, дискретную математику, можно будет создать программное обеспечение, решающее широкий круг задач: от доказательства теорем и сочинения стихов до шахматной игры, медицинской диагностики, государственного планирования.

Во многих случаях формализация процедур оценки ситуации и выработки решения оказалась очень сложной. Их программная реализация, создание детальных инструкций для гигантского числа возможных ситуаций, с которыми может встретиться компьютерная система, также требует очень больших затрат. Ряд экспертов оценивали объем работы по созданию такой системы в сотни тысяч человеко-лет работы высококвалифицированных разработчиков.

Это заставило искать новые принципы и по-новому взглянуть на поразительную способность человеческого мозга ориентироваться в незнакомой, не встречавшейся ранее ситуации, управлять движением, принимать быстрые и достаточно точные решения, распознавать образы. В самом деле, трехлетний ребенок с легкостью отличает кошку от собаки в жизни, на картинке, при разном освещении. Для компьютерных программ это нерешенная проблема. Второе обстоятельство, способствовавшее бурному развитию нейронауки и большому интересу к ней, — успехи биологии. В последние сорок лет стало ясно, как в ряде важных случаев проходится путь от взаимодействия отдельных молекул до реакции организма как целого. На новом уровне, связанном с развитием молекулярной биологии, стала ясна универсальность многих биологических механизмов. Появилась надежда, что благодаря новым методам, инструментам, идеям этот путь может быть пройден и для процессов, связанных с восприятием, сознанием, психикой.

Наконец, развитие точных наук, успехи в исследовании нелинейных математических моделей помогли сформулировать новые идеи в этой области. Основная идея состоит в том, что восприятие, обучение, мышление, другие функции мозга обусловлены коллективным процессом, приводящим к согласованной работе ансамблей достаточно просто устроенных нервных клеток — нейронов. Самоорганизация («самопрограммирование») таких ансамблей и является ключом к объяснению функций мозга. Работы по исследованию памяти человека и животных показали, что нельзя выделить в мозге одной четко локализованной структуры, отвечающей за запоминание. Это заставляет предположить, что мы имеем дело с распределенной системой. Простым физическим прообразом ситуации, которая, вероятно, имеет место, является голограмма.

---