Добавлен: 09.12.2023
Просмотров: 61
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Рис. 2. Голограмма
Голограмма дает возможность записывать и хранить информацию с помощью когерентных пучков света. Принцип ее получения — запись на фотопластинке интерференционной картины, возникающей при наложении падающего и рассеянного фиксируемым объектом монохроматического излучения. Если осветить зафиксированную на фотопластинке интерференционную картину лучом того же лазера, то он при рассеянии даст изображение первоначального объекта. При этом информация о данной точке на поверхности объекта оказывается «рассредоточенной» по всей поверхности фотопластинки-голограммы.
Испортив часть голограммы, мы не утратим изображение объекта, а лишь сделаем его менее четким. Это кардинально отличается от организации стандартной «фотографической» памяти. Отрезав и выбросив кусок фотографии, мы утратим возможность узнать, что на нем было запечатлено.
Хаос в нелинейной динамике [5]
В мире есть порядок и упорядоченные в той или иной степени системы и структуры, есть непорядок, есть беспорядок и случайные явления, есть хаос, т.е. беспорядок в абсолюте.
Рис. 3. Символ хаоса. Символ порядка не придуман.
Порядок и хаос – это и противоположные, и взаимодополняющие понятия. Здесь имеет место единство противоположностей, равновесие (или неравновесие) между которыми определяет направление и темп развития или деградации структур в рассматриваемой системе.
Важно понимать, что во Вселенной господствует беспорядок, локально упорядоченный во времени и/или в пространстве, со случайными процессами, которые частично предопределены и даже закономерны. Но не все и не всегда: правит нами случай.
Хаос, детерминированный хаос, беспорядок, непорядок, бардак и т.п. – термины, обозначающие обычно некоторые общие свойства. Но не всегда. Часто это никак не связанные понятия: хаос к беспорядку никакого отношения может не иметь, а детерминированный (динамический) хаос - символ высшего порядка.
Под классическим (идеальным, недерминированным, статистическим, стохастическим) хаосом понимают полный (идеальный) беспорядок, полностью разупорядоченную структуру (например, аморфное тело, на рентгенограмме которого нет каких-либо рефлексов), неупорядоченное, случайное, непрогнозируемое поведение элементов системы, процесс, описываемый чисто статистическими законами (например, броуновское движение, белый шум и т.п.). Процесс статистического хаоса не помнит своей истории и его будущее не определено. Для таких процессов понятия аттрактор не существует.
Беспорядок – отсутствие или нарушение порядка, упорядоченности системы, последовательности в чем-либо.
Хаос – это состояние беспорядка и нерегулярности. Хаотические процессы можно подразделить на два вида: случайные процессы и хаотические процессы.
В хаотическом режиме статистические закономерности определяются числом степеней свободы. Хаос – это отражение сложного поведения большого количества частиц, которые, сталкиваясь, создают картину неупорядоченного поведения. Примерами хаотических процессов являются: метание шарика в рулетке, броуновское движение частицы под случайными ударами «соседей», беспорядочные вихри турбулентности, образующиеся при течении жидкости с достаточно большой скоростью, диффузия и т.п. В броуновском движении молекул в газовой или жидкой среде имеет место хаотические тепловые перемещения громадного числа молекул (частиц), случайным образом ударяющих по другим молекулам (частицам), вынуждая их к случайным блужданиям. Такой процесс оказывается полностью непредсказуемым, недетерминированным, поскольку точно установить последовательность изменений в направлении движения частицы невозможно. Из этого следует невозможность выведения таких закономерностей, которые позволяли бы точно прогнозировать каждое последующее изменение траектории частицы по предыдущему ее состоянию. Здесь нельзя связать между собой причину и следствие. Однако некоторые усредненные характеристики поведения в состоянии недетерминированного хаоса можно найти, например, расстояние, пройденное частицей за некоторое время.


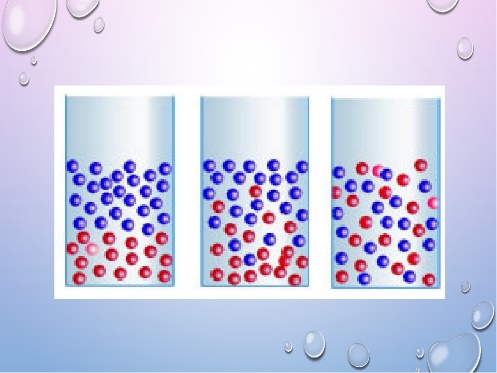
Рис. 4. Примеры хаотических процессов.
Случайный процесс (вероятностный, стохастический) – семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты; поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны, так и случайными. На практике часто встречаются случайные процессы, протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причём ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени. Такие случайные процессы называются стационарными. Любое развитие процесса во времени (неважно, детерминированное или вероятностное) при анализе в терминах вероятностей будет случайным процессом (иными словами, все процессы, имеющие развитие во времени, с точки зрения теории вероятностей, стохастические).
Случайные процессы удобно рассматривать с точки зрения теории вероятности, а также использовать понятие бита из информатики. Подбрасывание монеты - случайный процесс, с 2-мя исходами, вероятность =50%, энтропия (и информация) 1 бит. Чтобы узнать исход броска монеты требуется количество информации 1 бит. Подбрасывание монеты n раз, приводит к случайной последовательности с энтропией равной n бит. В случае броска монеты известно, что следующий бит будет либо нулем (орел), либо единицей (решка), но не более того: монета абсолютно непредсказуема. В этом случае случайно возникшая цепочка битов содержит количество информации, равное ее длине. Но предположим, что монета, которую мы используем, фальшивая, и на вероятность выпадения орла приходится 70%. В этом случае каждый бит будет содержать немного меньше информации, поскольку мы знаем, что более вероятно выпадение орла. Крайний случай – это цепочка, состоящая из единиц. Если мы знаем, что при броске всегда выпадает решка, то, подбрасывая монету, не получаем вообще никакой информации. Здесь цепочка битов полностью предсказуема, содержание информации в ней нулевое.
Изучение хаоса с точки зрения нелинейной динамики позволило пролить свет на некоторые физические явления, так как философия восприятия этих явлений была модифицирована.

Рис. 5. Пример случайного процесса
Заключение
Нелинейная динамика является методом исследования в естественных науках. Она вытекает из линейной динамики, однако сильно рознится с ней в силу усложненных методов в вычислении тех или иных физических и математических величин. Сама по себе нелинейная динамика – это раздел математики, который рассматривает нелинейные динамические (или изменяющиеся во времени) системы.
Описанный раздел в математике дал мощный толчок к развитию технологий, таких как нейронные сети, голография, искусственный интеллект, компьютерное моделирование, что в ассоциации говорит о развитии нейронауки.
Описанное выше изучение хаоса так же не осталось бесполезным в естественных науках. Изучение Вселенной как беспорядочной и недетерминированной позволило описать некоторые физические явления, такие как броуновское движение, турбулентное движение в жидкости, диффузия в жидкости и газах и др. Они являются примерами хаотического движения.
Однако некоторые примеры хаоса, а именно случайные процессы, можно описать с помощью математической статистики и теории вероятности, стремительное развитие которых также произошло вместе с нелинейной динамикой. Примерами случайных процессов служат бросание игральных костей, подбрасывание монетки, теория игр и др.
Таким образом, развитие нелинейной динамики позволило эволюционировать многим дисциплинам в естественных науках, технике и философии. Прогресс в этой области позволил еще на один шаг приблизиться к познанию человечеством Вселенной.
Список литературы:
-
Пример нелинейной динамики в электротехнике // Бычков Ю. А., Золотницкий В. М., Чернышев Э. П. Основы теоретической электротехники: учебное пособие. 2-е изд., стер. – СПб.: Издательство «Лань», 2009. – 592 с. -
Определение нелинейной динамики // Данилов Ю. А. Лекции по нелинейной динамике. — М.: Постмаркет, 2001. — 184 с., https://obuchalka.org/2013101173942/lekcii-po-nelineinoi-dinamike-elementarnoe-vvedenie-danilov-u-a-2006.html, (дата обращения: 5.12.2022, 16:00) -
Динамические системы как метод нелинейной динамики // Анищенко В. С., Вадивасона Т. Е. Лекции по нелинейной динамике: учеб. пособие для вузов. - М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2011.- 516 с., https://www.rulit.me/data/programs/resources/pdf/Anishchenko_Lekcii-po-nelineynoy-dinamike_RuLit_Me_620800.pdf, (дата обращения: 5.12.2022, 16:16) -
Нейронные сети // Малинецкий Г. Г., Потапов А. Б. Современные проблемы нелинейной динамики. — М.: Эдиториал УРСС, 2000. — 326 с., https://obuchalka.org/20220221141447/sovremennie-problemi-nelineinoi-dinamiki-malineckii-g-g-potapov-a-b-2000.html, (дата обращения: 5.12.2022, 16:23) -
Хаос в нелинейной динамике // Игорь Н. фон Бекман Нелинейная динамика сложных систем: теория и практика http://profbeckman.narod.ru/NelDin/NelDinText.pdf (дата обращения: 5.12.2022, 16:32)