_{II БӨЛІМ}
Ықтималдықтар теориясы және математикалық статистика
I тарау. Кездейсоқ оқиғалар
§1. Негізгі түсініктер. Оқиғалардың түрлері
Кездейсоқ құбылыстардың заңдылықтарын зерттейтiн математиканың негiзгi салаларының бiрi ықтималдықтар теориясы болып табылады. Күнделiктi өмiрде бiз әртүрлi оқиғалардың куәсi болып отыратынымыз белгiлi. Мысалы, математика сабағынан тест бойынша емтихан тапсырып жақсы баға аласыз. Бұл-оқиға. Көлемдерi бiрдей ақ және көк шарлар жәшiкке салынған. Егер жәшiктен кез келген шар алсақ ол не ақ, не көк түстi болуы мүмкiн. Бұл да оқиға. Күмiс теңгенi лақтырсақ не елтаңба, не цифр жазылған жағы шығады. Бұл да оқиғалар. Ал ойын кубын лақтырсақ 6 оқиғаның бiрi шығады, себебi оның әр жағына 1,2,3,4,5 және 6 сандары жазылған.

Тәжірибелер, эксперименттер, бақылаулар, тексерулер, сұрақнама, референдум т.с.с жүргізулерді сынақ жүргізу деп атайды.

Осы мысалдардан оқиға белгiлi бiр жүргiзiлген сынақтың нәтижесiнде пайда болатынын көремiз. Сондықтан сынақ нәтижесiнде пайда болған кез келген дерек оқиға деп аталады. Сынақтың мысалдары: ойын сүйегiн (кубын) лақтыру, күміс теңге лақтыру, жәшiктегi әр түстi бiрдей шарларды бiр-бiрлеп алу т.с.с. Ал осы келтiрiлген тәжiрибелердегi пайда болатын оқиғалар: ойын кубының жақтарында жазылған сандар (1; 2; 3; 4; 5; 6); теңгенің сан жазылған немесе елтаңба жазылған жағы; жәшiктен әр түстi шарлардың алынуы. Әрине бұл тәжiрибелердiң нәтижелерiн алдын-ала болжау мүмкiн емес. Дегенмен, алғашқы екi тәжiрибелерде теңгенің сан жазылған жағы мен елтаңба жазылған жағының пайда болу мүмкiндiгi тең, сондай-ақ ойын сүйегiнiң сан жазылған кез келген жағының пайда болу мүмкiндiктерi де тең. Бiз мұндай болжамды теңгемен мен ойын сүйегiнiң симметриялылықтарын ескерiп, жасап отырмыз. Тәжірибе нәтижесінде белгілі бір оқиға пайда болуы да пайда болмауы да мүмкін. Осындай оқиғаларды кездейсоқ оқиғалар деп атайды. Кездейсоқ оқиғалардың мысалдары:

- теңге лақтыру сынағында елтаңбаның немесе санның пайда болуы;

- лотерея ойынында белгілі бір билетке ұтыс шығуы;

- ойнау деңгейлері бірдей екі футбол командасының кездесуінің нәтижесі.

Ал жалпы жағдайда оқиғалардың пайда болу мүмкiндiгiн бағалау үшiн оларды белгiлi бiр сандармен байланыстырады. Ол сандарды оқиғаның ықтималдығы деп атайды. Оқиғаның ықтималдығы Р(А) арқылы белгiленедi. Егер қарастырылып отырған тәжірибедегі оқиғалар жиыны төмендегi шарттарды қанағаттандырса:

1.Тәжiрибе нәтижесiнде әруақытта оқиғалардың бiреуi пайда болады;

---

2.Кез келген екi және бiрге пайда болмайды,

онда осы оқиғалардың жиынын элементарлық оқиғалар кеңiстiгi деп атайды және арқылы белгiлейдi. Әдетте немесе , яғни оқиғалары саны ақырлы немесе саналатын жиындары қарастырылады. Ал кеңiстiгiнiң ішкі жиындарын оқиғалар деп атайды.

Сонымен кез келген А оқиғасы кеңiстiгiнiң ішкі жиыны болып табылады, яғни А . Егер А= болса, онда А оқиғасы ақиқат оқиға деп аталады , демек ақиқат оқиға сынақ нәтижесінде міндетті түрде пайда болады. Тәжірибе нәтижесінде мүлде пайда болмайтын оқиға мүмкін емес оқиға деп аталады.Мысалы, ылғи көк шарлар салынған жәшіктен ақ шар алу, туған күніне сөйлейтін крокодил силау, ойын кубын лақтырғанда 7 санының пайда болуы,..., мүмкін емес оқиғалар болады.

Айталық ойын кубын лақтыру тәжiрибесi жүргізілсін, сонда , ал _i - цифрлар жазылған ойын кубының жақтарының пайда болуы, сол сияқты теңге лақтыру тәжiрибесiнде .

Ендi ойын кубын лақтырғанда пайда болатын кейбiр оқиғаларды қарастыралық:

- үш санына еселi цифр жазылған ойын

кубының жақтарының пайда болуы;

---

- тақ сан жазылған жақтың пайда болуы;
- жұп сан жазылған жақтың пайда болуы;
. Мұнда А₁ , А₂ және А ₃ -кездейсоқ оқиғалар, - мүмкiн емес оқиға себебі кубта 7 саны жазылған жақ жоқ, - ақиқат оқиға, себебі сынақ нәтижесінде оқиғаларының біреуі міндетті түрде пайда болады.

Енді қарастырылып отырған тәжiрибеге байланысты элементарлық оқиғалар кеңiстiгi белгiлi болсын ( ) делік. Осы тәжiрибеде пайда болатын кез-келген А оқиғасы осы - ның ішкі жиыны болатыны белгілі, яғни А . А оқиғасының құрамына кіретін элементарлық оқиғалар А оқиғасына қолайлы элементарлық оқиғалар деп аталады. Тәжірибе нәтижесінде А және В оқиғалары бірге пайда бола алмаса, онда олар үйлесімсіз оқиғалар деп аталады, ал егер бірге пайда бола алса, онда олар үйлесімді оқиғалар деп аталады. Мысалы, А,В,С,D,Е және Ғ оқиғалары ойын кубын лақтырғанда сәйкес 1,2,3,4,5 және 6 сандарының пайда болуын білдірсе, онда бұл оқиғалар үйлесімсіз оқиғалар болып табылады, ал егер L оқиғасы ойын кубын лақтырғанда жұп ұпайдың пайда болуын білдірсе, онда L оқиғасы В,D,Ғ оқиғаларымен үйлесімді болады да, ал А,С,Е оқиғаларымен үйлесімсіз болады.

Екі А және В оқиғаларының біреуінің пайда болуы екіншісінің пайда болуына немесе пайда болмауына әсер етпесе , онда олар өзара тәуелсіз оқиғалар деп аталады.Теңге лақтыру сынағындағы Е және С оқиғалары тәуелсіз оқиғалар. А және В оқиғаларының көбейтіндісі деп олардың бірге пайда болуын айтады және көбейтіндіні АВ арқылы белгілейді. Айталық ойын кубын лақтыру сынағында А-жұп санның пайда болуы болсын, ал В- үш санына еселі санның пайда болуы болсын, С- алты санының пайда болуы болсын. Сонда С оқиғасы А және В оқиғаларының көбейтіндісі болып табылады.

---

А және В оқиғаларының қосындысы деп не А, не В немесе АВ оқиғаларының пайда болуын айтады. Алдыңғы мысалда А+В оқиғасы 2,3,4,6 сандарының пайда болуын білдіреді. Егер А және В үйлесімсіз болса,онда А+В оқиғасы не А-ның, не В-ның пайда болуын білдіреді. Егер орындалса, онда A₁, A₂, ..., A_n оқиғалар жиыны оқиғалардың толық тобы деп аталады, яғни олардың қосындысы ақиқат оқиға. Жоғарыда қарастырылған мысалда A₂, A₃ оқиғалары толық топ құрайды, себебi A₂ +A₃ = . Осыдан тәжірибе нәтижесінде толық топ құратын оқиғалардың біреуі міндетті түрде пайда болатынын көреміз.

Өзара үйлесімсіз және толық топ құратын екі оқиға карама-карсы оқиғалар деп аталады. Қарама-қарсы оқиға 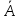әріпі арқылы белгіленеді.

Теңге лақтыру тәжірибесінде Е-елтаңбаның пайда болуы, ал С-санның пайда болуы болса , онда Е және С оқиғалары қарама-қарсы оқиғалар болады.

Егер элементарлық оқиғалар кеңiстiгiн тiктөртбұрыш ретiнде, ал оқиғаларды оның бөлiгi ретiнде бейнелесек, онда оқиғалардың қосындысын, көбейтiндiсiн және қарама-қарсы оқиғаларды төмендегiдей бейнелеп көрсетуге болады.



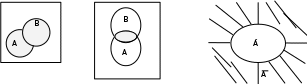
Сондай-ақ оқиғаларды қосу, көбейту амалдары төмендегi қасиеттердi қанағаттандырады:

1. 
   А + B = B + A 2.
   

3. (A+B) +С = А + (В+С) 4.

5. 
   
   

Осыдан төмендегi теңдiктердiң орындалатындығы шығады:

А+А=А, AA=A, A+ = , A =A, A+ =,

---

Жалпы "ықтималдық" ұғымына бiрнеше түсiнiк берiледi. Соның бiрi - ықтималдықтың классикалық анықтамасы.

Қазiргi кезеңде ықтималдықтар теориясы жиындар теориясының негiзгi ұғымдарын пайдаланып, аксиоматикалық түсiнiк негiзiнде құрылады. Сондықтан төменде жиындар теориясының негiзгi ұғымдары келтiрiлген. Жиындар элементтерiнiң сандарына байланысты ақырлы жиындар, ақырсыз жиындар болып бөлiнедi. Егер ақырсыз жиындардың элементтерiн белгiлi бiр ретпен санауға болатын болса, онда ондай жиындар саналатын жиындар деп аталады. Натурал сандар жиыны саналатын жиынның мысалына жатады. Екi жиынның сәйкес элементтерi өзара тең болса, онда ол жиындар тең жиындар немесе эквиваленттi жиындар деп аталады (А=В). Егер В жиынының әрбiр элементi А жиыннына кiретiн болса, онда В жиыны А жиынының iшкі жиыны деп аталады (сурет I).

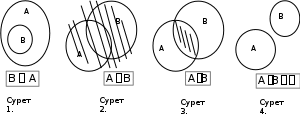
А және В жиындарының барлық элементтерiнен құрылған жиынды А және В жиындарының қосындысы /С=А+В/ деп атайды

/сурет 2/.

А және В жиындарына ортақ элементтерден құрылған жиынды осы жиындардың көбейтiндiсi /С= / деп атайды /сурет 3/. Өзара қиылыспайтын А және В жиындарына сәйкес оқиғалар үйлесiмсiз оқиғалар деп аталады, яғни АВ= (сурет 4). Ал егер болса, онда бұл оқиғалар қос-қостап үйлесiмсiз оқиғалар деп аталады.

Оқиғаның ықтималдығы Р(А) төмендегi аксиомаларды қанағаттандырады:

1.Кез-келген оқиғаның ықтималдығы нөлмен бiрдiң арасында болады:
0  P(A)  1 (1.1.1)

2. Ықтималдықтарды қосу аксиомасы:

Егер А және В үйлесiмсiз оқиғалар болса, онда
Р(А+В) = Р(А) + Р(В) (1.1.2)

Егер A₁, A₂, ..., A_n үйлесiмсiз оқиғалар болса, онда (1.1.3) аксиома орындалады:
(1.1.3)

3.Саналатын оқиғалар жиыны үшiн ықтималдықтарды қосу аксиомасы:

Егер A₁, A₂, ..., A_n, ... оқиғалары үйлесiмсiз болса, онда
(1.1.4)
Егер элементарлық оқиғалардың ықтималдықтары белгiлi болса, онда ықтималдықтар теориясының аксиомаларының көмегiмен кез-келген оқиғаның ықтималдығын есептеуге болады. Алайда бұл аксиомалардың элементарлық оқиғалардың ықтималдықтарын анықтауға ешбiр көмегi жоқ. Ал элементарлық оқиғалардың ықтималдықтары жүргiзiлiп отырған тәжiрибенiң ерекшелiктерiн пайдаланып анықталады.

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx