Мысалы, жоғарыда қарастырылған тәжiрибелерде:

1.P(₁)= P(₂)=0,5 - бұл теңгенің жақтарының пайда болуларының ықтималдықтары;

2. P( _i )=1/6, i =1,2,…,6 - бұл ойын кубының цифр жазылған жақтарының пайда болуының ықтималдықтары.

Бұл ықтималдықтар теңге мен ойын кубының симметриялығын пайдаланып анықталып отыр.

Егер A₁, A₂, ..., A_n оқиғалары үшiн P(A₁)= P(A₂)=...= P(A_n) орындалса, онда бұл оқиғалар теңмүмкiндiкті оқиғалар деп аталады.

Айталық элементарлық оқиғалар кеңiстiгi  теңмүмкiндiкті оқиғалардың жиыны болсын, яғни

1. P(₁)= P(₂)=...= P(_n)

= - толық топ.

Олай болса,

(1.1.5)

Егер _i  A (i= , кn), онда _i- элементарлық оқиғалары А оқиғасына қолайлы элементарлық оқиғалар болып табылады.

Анықтама (ықтималдықтың классикалық анықтамасы). Берiлген тәжiрибедегi теңмүмкiндiкті элементарлық оқиғалар кеңiстiгiнiң А оқиғасына қолайлы оқиғалар санының осы кеңiстiктiң барлық элементарлық оқиғалар санына қатынасы А оқиғасының ықтималдығы деп аталады.

Бұл анықтамадан

P(A)=m/n (1.1.6)

формуласын аламыз. Mұндағы m - А оқиғасына қолайлы теңмүмкіндікті элементарлық оқиғалар саны, n - теңмүмкіндікті элементарлық оқиғалар кеңiстiгiнiң барлық оқиғалар саны. Осы анықтамадан (1.1.6) формула негiзiнде

m=n болса, А= болады да, Р(А)=Р()=1 аламыз, яғни ақиқат оқиғаның ықтималдығы 1-ге тең, ендi m=0 болса, онда А мүмкiн емес оқиға, демек Р(А)=0, яғни мүмкiн емес оқиғаның ықтималдығы нөлге тең. Әдетте ақиқат оқиғаны - U, ал мүмкiн емес оқиғаны - V арқылы белгiлейдi, яғни Р(U)=1, P(V)=0. Сонымен кез-келген оқиғаның ықтималдығы нөл мен бiрдiң арасында болады:

0  P(A)  1

1-мысал.Айталық А,В,С тәжірибедегі кез келген оқиғалар болсын.
Мына ,

оқиғаларының мағынасы қандай?

Шешуi: А₁ оқиғасы А,В және С оқиғаларының бiрге пайда болуын бiлдiредi; А

---

₂ - А,В және С оқиғаларының ешқайсысының пайда болмағандығын көрсетедi. А₃ - және оқиғаларының ең болмағанда бiреуiнiң пайда болатындығын бiлдiредi .

А₄ - А,В және С оқиғаларының тек қана бiреуiнiң пайда болатындығын көрсетедi; А₅ - А,В,С оқиғаларының тек қана бiреуi пайда болады немесе пайда болады, яғни А₅=А₂+А₄.

2-мысал. Мерген нысанаға екi рет оқ атты. А_i- i-шi атқанда нысанаға тигiзуi (i= ). Ендi мына А - ең болмаса бiр рет тигiздi, В - бiр рет қана тигiздi, С - екi рет тигiздi, D - екi рет тигiзе алмады оқиғаларын А₁, А₂ оқиғалары арқылы өрнекте.

Шешуi: А₁,A₂ - сәйкес бiрiншi және екiншi атқанда нысанаға тигiзуi, ал және - сәйкес бiрiншi, екiншi атқанында нысанаға тигiзе алмауы.

Сонда А₁+А₂ оқиғасы, екi оқиғаның қосындысының анықтамасы бойынша не А₁ не А₂ немесе А₁А₂ оқиғаларының пайда болатынын, яғни ең болмағанда бiр оқиғаның пайда болатынын көрсетедi, олай болса А=А₁+А₂.

Сол сияқты В= - тек бiр рет нысанаға тигiзу; С= - нысанаға екi рет тигiзу; D= - екi рет тигiзбеуi.

3-мысал . Урнаға 4 ақ, 9 қара және 7 қызыл бiрдей шарлар салынған. Урнадан кез-келген бiр шар алынады. Сонда ақ шар пайда болуының ықтималдығы қандай?

Шешуi: А - ақ шар пайда болуы болсын. Бұл тәжiрибеде элементарлық 

---

_i (i= ) - оқиға дегенiмiз - урнадан кез-келген бiр шар алу. Шарлар бiрдей болғандықтан бұл _i оқиғалары теңмүмкiндiкті және өзара үйлесiмсiз. Элементарлық оқиғалардың жалпы саны осы урнадағы шарлар санына тең n=20, ал А оқиғасына қолайлы элементарлық оқиғалары саны урнадағы ақ шарлар санына тең. Сондықтан ықтималдықтың анықтамасы бойынша:

;

Ықтималдықтың классикалық анықтамасы сынақтардың нәтижелерiнiң саны ақырлы элементарлық оқиғалар болған жағдайда ғана қолданылады. Нәтижелерi элементарлық оқиғалар болып келетiн сынақтарда көбінесе симметриялық қасиет бар болады. Мысалы, ойын кубын лақтыру сынағында ойын кубы симметриялы. Ал, сынақтар нәтижелерi элементарлық оқиғалар арқылы өрнектелмеген жағдайда ықтималдықтың классикалық анықтамасын қолдануға болмайды. Сондықтан осындай жағдайларда ықтималдықтың басқа анықтамасы қолданылады.

Анықтама.'>Анықтама. Жүргiзiлген n сынақтарда А оқиғасының пайда болуының салыстырмалы жиiлiгiн оның статистикалық ықтималдығы деп атайды.

Бұл анықтаманы оқиғаның ықтималдығының статистикалық анықтамасы деп атайды.

Статистикалық ықтималдық арқылы белгiленедi. Сонда ,

мұнда W(A) -оқиғаның салыстырмалы жиiлiгi, n - жүргiзiлген сынақтар саны, m- осы сынақтарда A оқиғасының пайда болған саны(m-оқиғаның жиілігі).

Статистикалық ықтималдықтың қасиеттерi оқиғаның P(A) - ықтималдығының қасиеттерiмен бiрдей болады.

Белгiлi бiр шарттар комплексi орындалып тәжiрибе жүргiзгенде әруақытта А оқиғасы пайда бола алатын болса ғана ықтималдықтың статистикалық анықтамасын қолдануға болады. Сондай-ақ, оқиғалардың салыстырмалы жиiлiктерiнiң тұрақтылығы сақталуы керек, яғни, әртүрлi сынақтар сериясының нәтижесiнде оқиғаның салыстырмалы жиiлiгi шамалы ғана өзгерiп белгiлi бiр тұрақты санға жуықтап тең болуы шарт. Сынақтар саны мейiлiнше көп болуы керек. Мiне, осы талаптар орындалғанда ғана, ықтималдықтың статистикалық анықтамасын қолдануға болады.

Сонымен, оқиғаның статистикалық ықтималдығы сынақтар жүргiзiлiп бiткеннен соң есептеледi және ол оқиғаның ықтималдығына жуықтап тең болады.

---

4-мысал. Урнаға 4 ақ, 5 көк және 11 қызыл түстi бiрдей шарлар салынған. Үш сынақтар сериясы жүргiзiлсiн: n₁ = 10 - бiрiншi сынақта алынған шарлар саны, n₂= 15 - екiншi сынақта алынған шарлар саны және n₃ = 17 - үшiншi сынақта алынған шарлар саны.

Егер бiрiншi сынақта түстi шарлар m₁ = 7 рет, екiншi сынақта m₂ = 10 рет, ал үшiншi сынақта m₃ = 14 рет пайда болғаны белгiлi болса, онда А-түстi шарлардың (көк немесе қызыл түсті шарлар)пайда болуы оқиғасының статистикалық ықтималдығы қандай болады?

Шешуi: Есептiң шартынан екенiн анықтаймыз.

Осы мысалдан оқиғаның статистикалық ықтималдығы әрбiр сынақта әртүрлi болатынын көремiз. Екiншi жағынан, оқиғаның статистикалық ықтималдығы сынақтар саны өскен сайын белгiлi бiр тұрақты санға мейiлiнше жақындайтындығы да байқалады. Ондай сан оқиғаның ықтималдығы болып табылады. Қарастырып отырған мысалда P(A) = 0,8.

Сондықтанда оқиғаның классикалық анықтамасымен қатар статистикалық анықтамасы да қолданылады.

5-мысал. Күмiс теңге 8 рет лақтырылғанда “елтаңба” 3 рет пайда болды. Елтаңбаның пайда болуының статистикалық ықтималдығы қандай?

Шешуi: Сынақтар саны n = 8, ал елтаңбаның пайда болған саны m = 3. Сондықтан елтаңбаның пайда болуының статистикалық ықтималдығы былай табылады .

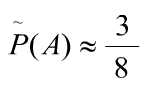
Ықтималдықтың классикалық анықтамасын қолданып А оқиғасының ықтималдығын тапқанда осы оқиға пайда болатын сынақтар сериясындағы барлық теңмүмкіндікті элементарлық оқиғалар санын, сондай-ақ, А оқиғасына қолайлы элементарлық оқиғалар санын есептеуге тура келедi. Ал нақты есептер шығарғанда осындай элементарлық оқиғалар санын табу кейбiр есептер үшiн едәуiр қиындықтар туғызады. Осындай жағдайларда элементарлық оқиғалар санын табуға комбинаторика формулаларын қолданады.

Табиғаты әртүрлi бiртектi элементтерден құрылған комбинациялардың санын табу әдiстерiн зерттейтiн математиканың бiр саласы комбинаторика деп аталады.

Айталық бiртектi әртүрлi n элементтер жиыны берiлсiн. Осы n элементтерден құрамында k элемент болатын әртүрлi комбинациялар құруға болады.

6-мысал. Берiлген әртүрлi үш а, b, с элементтерiнен әртүрлi комбинациялар құр.

Шешуi: Мұндай комбинациялардың үш түрi болады, яғни,

---

k = 1, k = 2, k =3 жағдайлары қарастырылады:

а) Егер k = 1 болса, онда берiлген үш элементтен бiр-бiрден үш комбинация құрылады: а; в; с.

б) Егер k = 2 болса, онда мына комбинациялар алынады: аb, bс, ас, bа, сb, са.

в) Егер k = 3 болса, онда аbс, асb, саb, сbа, bса, bас 6 комбинацияларын аламыз.

Анықтама. Берiлген әртүрлi n элементтен m элемент бойынша орналастырулар деп, әрқайсысы бiр-бiрiнен не құрамы бойынша, не орналасу ретi бойынша ажыратылатын комбинацияларды айтады.

Орналастырулардың жалпы саны мына формуламен анықталады

(1.1.7)

Мұндағы, , сондай-ақ 0! = 1 деп қабылданған. n!-”эн факториал” деп оқылады.

7-мысал. Үш элементтен екi элемент бойынша орналастырулар санын тап, яғни -нi тап.

Шешуi: (7) формуланы қолданамыз



Алдыңғы мысалда да осы нәтиже алынған едi.

Анықтама. Берiлген n элементтен n элемент бойынша алмастырулар деп, әрқайсысы бiр-бiрiнен тек орналасу ретi бойынша ажыратылатын комбинацияларды айтады.

Алмастырулардың жалпы саны мына формуламен анықталады:

P_n = n(n - 1)…(n – n +1) = n! (1.1.8)

8-мысал. Төрт кiтапты кiтап сөресiне қанша жолмен орналастыруға болады?

Шешуi: Мұндай орналастырулардың саны (8) формуламен анықталады

P₄ = 4! = 24

Анықтама. Берiлген әртүрлi n элементтен к элемент бойынша терулердеп, әрқайсысы бiр-бiрiнен тек құрамы бойынша ажыратылатын комбинацияларды айтады.

Терулердiң жалпы саны мына формуламен анықталады

(1.1.9)

9-мысал. 5 оқушыдан 2 оқушыны кезекшiлiкке неше жолмен жiберуге болады?

Шешуi: 5 оқушыдан 2 оқушыны кезекшiлiкке жiберу жолдары 5 элементтен 2 элемент бойынша терулер санына тең. Себебi, бұл комбинациялар бiр-бiрiнен құрамдары бойынша ажыратылады. Демек, (9) формуланы қолданып 5 оқушыдан 2 оқушыны кезекшiлiкке жiберудiң

---

Смотрите также файлы

• Программа среднего профессионального образования 40. 02. 01 Право и организация социального обеспечения Дисциплина Физическая культура (2 семестр) Практическое задание 7.doc

• Родной язык Вопросы к промежуточной аттестации.docx

• Все чаще в современном обществе на различных уровнях затрагивается проблема ухудшения состояния здоровья нации.docx

• Влияние вредных привычек на организм человека.odt

• Существуют философские, социологические и психологические представления о проблеме ценностеи и ценностных ориентации.docx