Занятие 15. Практическая работа №3 «Расчет параметров

электрических цепей (однофазных), построение

векторной диаграммы»
Цель работы: по предложенной выше методике научиться определять параметры однофазных цепей и строить векторные диаграммы.

При решении задач необходимо пользоваться примерами решений, данными в теории однофазных цепей переменного тока. При решении задач можно пользоваться различными методами: аналитическим, векторным, комплексными числами. Их использование диктуется условиями задачи.

Для закрепления и проверки усвоения материала однофазных цепей переменного тока Вам необходимо решить несколько задач. Решение этих задач надо дать в письменном виде на платформе Ipsilon.
образЦЫ РЕШЕНИЯ ЗАДАЧ НА РАСЧЕТ ОДНОФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА.
Задача. Чему равна амплитуда силы тока в цепи переменного тока частотой 50 Гц, содержащей последовательно соединенные активное сопротивление

R = 1 кОм и конденсатор емкости С = 1 мкФ, если действующее значение напряжения сети, к которой подключен участок цепи, равно 220 В?

Решение

Запишем закон Ома для цепи переменного тока:

I = U / Z

Z – полное сопротивление цепи, которое складывается из активного и реактивного сопротивлений.

Z = √R²+Х²_с ;

Х_С = 1 / 2*3,14 f C (Ом) . Х_С = 3,18 Ком.

Найдем полное сопротивление, подставив в формулу данные из условия:

Z =3,3 КОм

Далее по действующему значению напряжения найдем амплитудное:

U_m = Uд⋅ √2 = 220⋅ √2 = 310 В

Теперь подставим апмлитудное значение напряжения в выражение для закона Ома и вычислим силу тока:

I_m= U_m / Z= 310 / 3300 = 0,09 А

Ответ: 0,09 А.

Пример решения задачи на расчет неразветленной цепи.
Задача: Последовательно с катушкой, активное сопротивление которой R₁=10 Ом и индуктив­ность L= 0,0318 Гн, включен прием­ник, обладающий активным сопро­тивлением R₂=1 Ом и емкостью С = 796 мкф (рис. I). К цепи при­ложено переменное напряжение, изменяющееся по закону

---

u=169,8·sin(314·t).






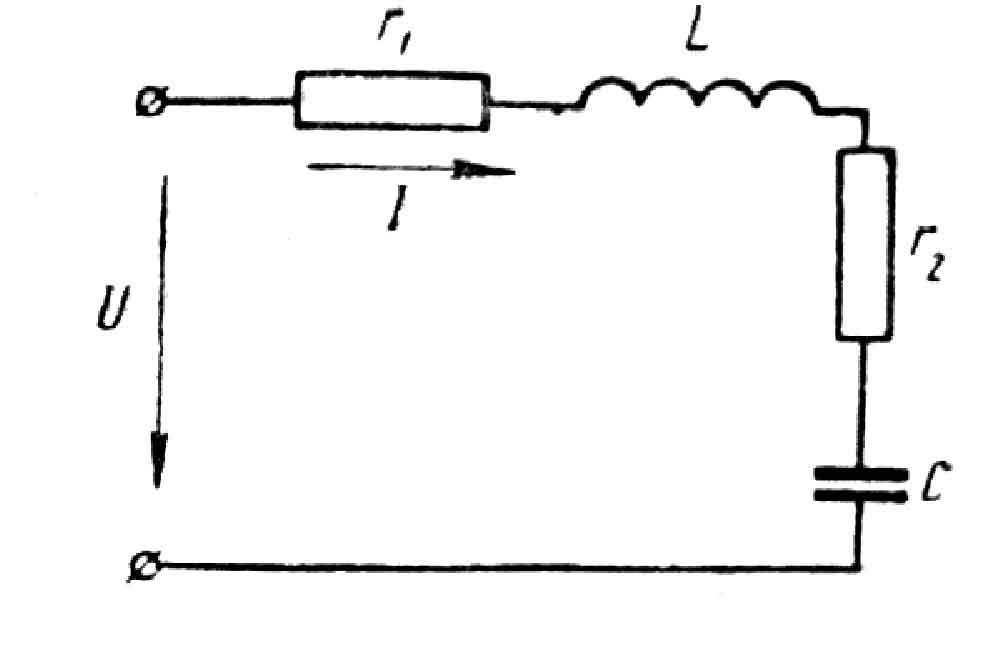
Рис. 1.

Определить: полное сопротив­ление цепи, коэффициент мощно­сти цепи, ток в цепи, активную, реактивную и полную мощности, а также построить в масштабе векторную диаграмму.

Как нужно изменить величину емкости, чтобы в цепи наступил резонанс напряжений? Индуктивность катушки остается постоянной.

Решение:
1. Определяем действующее напряжение U из уравнения

u=169,8·sin(314·t).


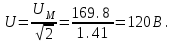
ω=2π·f=314 (1/сек).
Частота тока


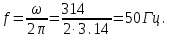
2. Индуктивное сопротивление катушки

X_L = ωL = 2π·f·L = 2·3.14·50·0.0318 = 10 Ом.

3. Емкостное сопротивление конденсатора



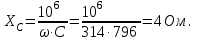
4. Полное сопротивление цепи



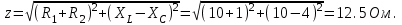
5. Коэффициент мощности цепи



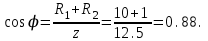
φ= arccos 0,88 =28 ⁰
6. Сила тока в цепи



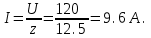
7. Активная мощность

P = I² (R₁+R₂) = 9.6² (10+1) = 1014 Bт.

или

P = U · I · cos φ = 120·9.6·0.88=1014 Вт.

8. Реактивная мощность

Q= I² X_L-I²X_C = I² (X_L-X_C) = 9.6²(10-4) = 553 Вар.

или

Q = I·U·sin φ = 120·9.6·0.49 = 553 Вар.

9. Полная мощность

S = I² z = 9.6²·12.5 = 1152 ВА

или

S = U·I = 120·9.6 = 1152 BA

или


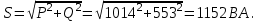
10. Построение векторной диаграммы начинаем с определения потерь напряжений на каждом сопротивлении:

U_R1=I·R₁=9.6·10=96(В);

U_R2=I·R₂=9.6·1=9.6(В);

U_L=I·X_L=9.6·10=96(В);

U_C=I·X_C=9.6·4=38.4(В);


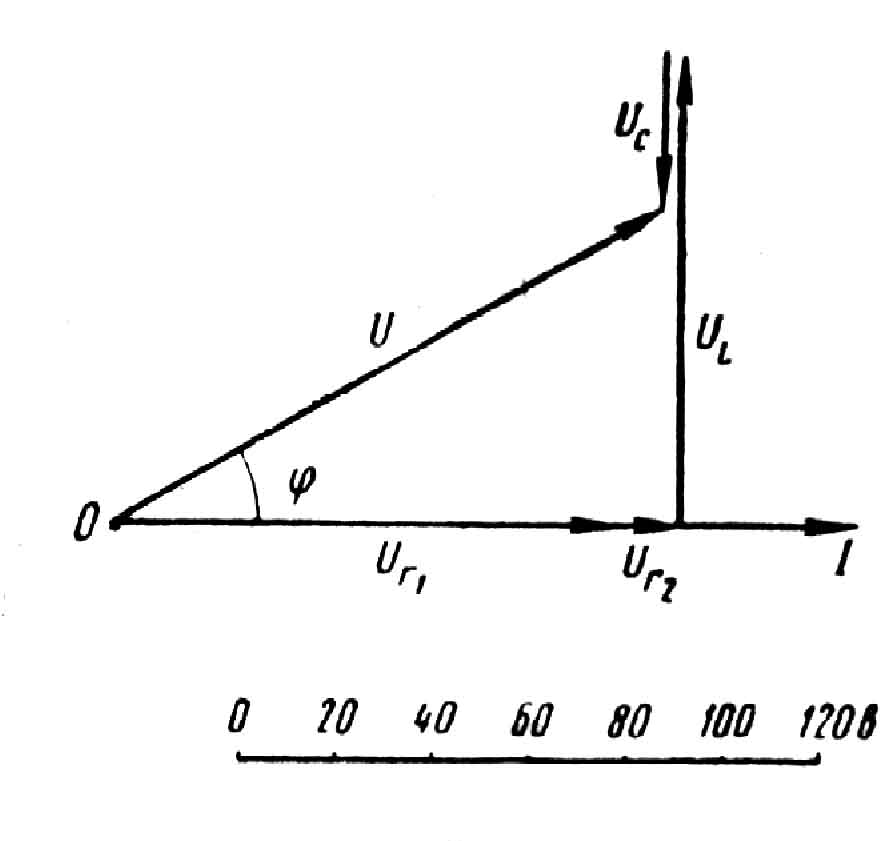
Рис.2

---

Затем выбираем масштаб для напряжений (см. рис. 2). Построение диаграммы начинаем с вектора тока I, который от­кладываем по горизонтали вправо от точки О (рис. 2). Вдоль векто­ра тока откладываем в принятом масштабе напряжения U_R1 и U_R2 теряемые в активных сопротивлениях цепи. Эти напряжения совпа­дают по фазе с током. От конца вектора U_R2 откладываем в сторону опережения вектора тока под углом 90° вектор потери напряжения U_L в индуктивном сопро­тивлении. Из конца векто­ра U_L откладываем вектор U_C в сторону отставания от вектора тока на угол 90^°. Геометрическая сумма че­тырех векторов равна пол­ному напряжению, прило­женному к цепи, т. е.
U = U_R1 + U_R2 + U_L + U_C.
11. Для получения ре­зонанса напряжений необ­ходимо, чтобы

Х_C = Х_L= 10 Ом, тогда 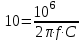, откуда 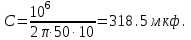При этом ток в цепи станет 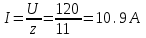, где .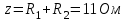

Пример решения задачи на расчет разветвленной цепи.
Задача: Катушка с активным сопротивлением R=20 Oм и ин­дуктивностью L= 0,0637 Гн соединена параллельно с конденсатором емкостью С =65 мкФ (рис. 3). Определить: токи в ветвях и в неразветвленной части цепи, ак­тивные мощности ветвей, углы сдвига фаз между током и напряже­нием первой и второй ветвей и всей цепи, если к цепи приложено напряжение U=100B, частота тока f = 50 Гц.

Как нужно изменить емкость во второй ветви, чтобы в цепи наступил резонанс токов? Построить векторную диаграмму.

R


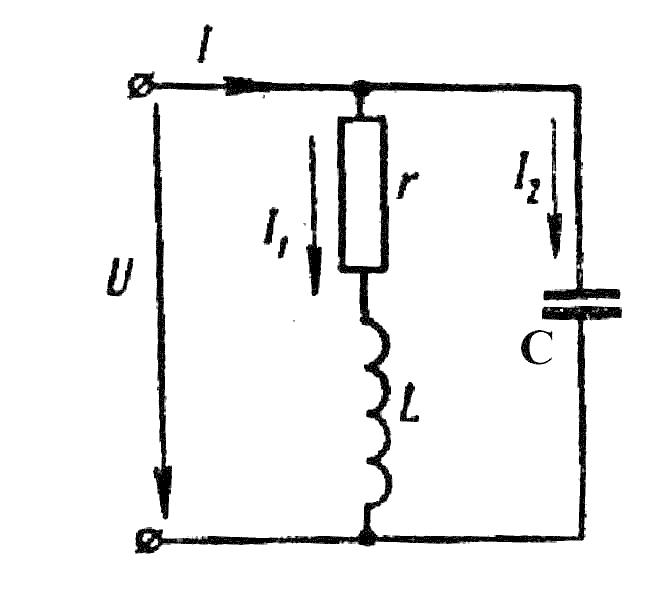
Рис.3.

Решение:
1. Индуктивное сопротивление катушки

X_L= ωL= 2π·f·L = 2·3.14·50·0.0637 =20 Ом.
2. Емкостное сопротивление конденсатора


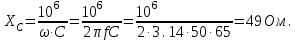
3. Токи в ветвях

---

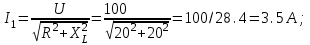
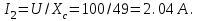
4. Коэффициенты мощности ветвей

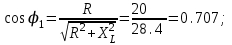
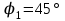(отстающий)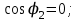

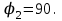(опережающий).
5. Активные и реактивные составляющие токов ветвей

;

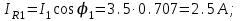
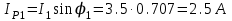I_R2=0; I_P2= 2.04·1.0 = 2.04 A.
6. Ток в неразвлетвленной части цепи



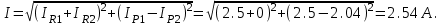
Реактивные токи ветвей должны вычитаться, так как реактивный ток ветви с емкостью принимается отрицательным.
7. Коэффициент мощности всей цепи



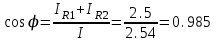
8. Активные мощности ветвей

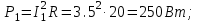P₂=0

Построение векторной диаграммы начинаем c вектора напряжения U (рис. 4). Под углом φ₁ к вектору напряжения (в сторону отста­вания) откладываем вектор тока I₁, под углом φ₂ (в сторону опере­жения) - вектор тока I₂. Геометрическая сумма этих векторов пред­ставляет ток I в неразветвленной части цепи. Проекции токов вет­вей на вектор напряжения являются активными составляющими I_R1 и I_R2; проекции этих токов на вектор, перпендикулярный вектору на­пряжения, - реактивными составляющими I_P1 и I_P2.

9. При резонансе токов ток I совпадает на фазе с напряжением, что возможно при равенстве реактивных токов ветвей I_P1=I_P2 (см. векторную диаграмму.

Тогда емкостное сопротивление этой ветви



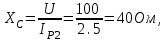
отсюда




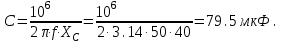
I_R1

---

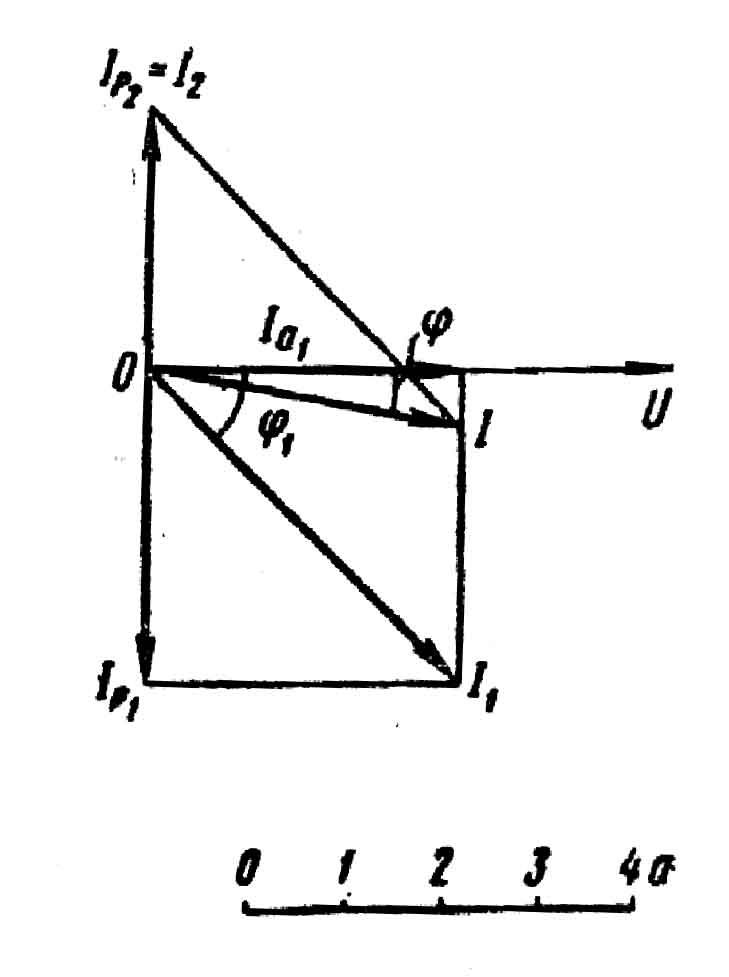
Рис. 4.
А сейчас Вы должны решить предложенные задачи и решение представить в письменном виде, грамотно оформленным, на платформе IPSILON.

Задача 1.

Катушка с ничтожно малым активным сопротивлением включена в цепь переменного тока с частотой 50 Гц. При напряжении 125 В сила тока равна

3 А. Какова индуктивность катушки?

Отв.: L = 0.13 Гн.
Задача 2.

В электрическую цепь переменного тока напряжением U = 220 В, частотой

f = 50 Гц включена катушка с индуктивностью L = 25,5 мГн и активным сопротивлением R = 6 Ом. Определить: X_L ; Z ; U_R ; Р; Q_L; cosφ. Цепь последовательная. Построить векторную диаграмму.

Отв.: X_L = 8 Ом; Z = 10 Ом; U_R = 132 В; Р = 2,9 КВт; Q_L = 3,87КВар;

cosφ = 0,6.
Задача 3.

К генератору переменного электрического тока с напряжением U = 240В и частотой f = 50Гц присоединен последовательно конденсатор с емкостью

C = 40 мкФ. Определить: 1) реактивное сопротивление емкости X_C; 2) ток в электрической цепи; 3) реактивную мощность цепи Q_С; 4) максимальную энергию, запасаемую в электрическом поле конденсатора W_С.

Отв.: X_C = 79,6 Ом; I = 3 А; Q_С = 723, 5 Вар; W_С. = 1,152 Дж.

Задача 4.

К цепи переменного тока (см. Рис. 1) приложено напряжение U = 12 В.

Индуктивное сопротивление X_L = 2,4 Ом, активное сопротивление R = 1 Ом.

Определить действующие значения токов в ветвях схемы I_{R ,} I_L, ток в цепи,

активную P, реактивную Q, полную S мощности, коэффициент мощности

cosφ.

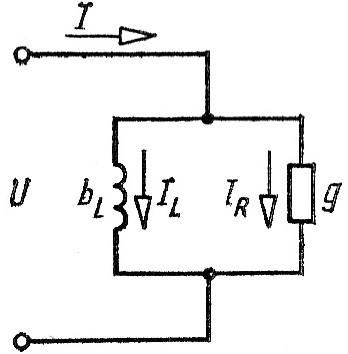Рис. 1.

Отв.:I_{R =} 12А; I_L = 5А; I= 13А; P =144В; Q=60Вар;S = 156 ВА;cosφ.= 0,92

Задача 5.

В электрической цепи (см. Рис.1) протекает ток I= 2,82 sin 314t (А).

Известны параметры цепи: активное сопротивление R = 24 Ом, емкостное сопротивление конденсатора Xс = 7 Ом. Определить действующее значение тока в цепи I_д, падение напряжения на участках цепи U_R и U_C , приложенное к цепи напряжение U, активную мощность P, реактивную мощность Q, полную мощность S. Записать выражения для мгновенных значений

---

Смотрите также файлы

• Федеральное агентство по образованию иркутский государственный технический университет.doc

• Компьютерная и интернет зависимости.docx

• Инженерная графика. Тест 1 1.pdf

• Лабораторная работа Математический маятник Цель работы изучение гармонических колебаний.docx

• В курсовом проекте так же учтены вопросы охраны труда и экологии.docx