Вариант 6

Цель работы:

• 
  Научиться составлять алгоритмы решения графических задач.
  

• 
  Научиться составлять алгоритмы и программы в соответствии с этими алгоритмами.
  

• 
  Научиться программированию на языке высокого уровня Pascal.
  

• 
  Изучить математический аппарат дисциплины «Компьютерная графика».
  

Постановка задачи:

Задание 1

Реализовать программу, строящую фрактал с заданными границами расчета 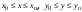. В таблице 1 каждому номеру варианта (№) соответствует вид фрактала и границы расчета.

Вариант	Вид фрактала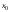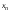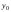
6	Джулия	–0.9	0.9	–1.1	1.0

Алгоритм построения множества Жюлиа




Шаг 0:

Выбрать параметр

Выбрать число M, которое считается бесконечно большим.

Положить , где - разрешающая способность экрана.

Для всех пар , где и выполнить следующую процедуру:

Шаг 1:

Положить

Шаг 2 (итерация):

---

Вычислить по , используя формулы





Увеличить счетчик k на 1.

Шаг 3 (оценка):

Вычислить .

Если , то выбрать цвет k и идти дальше на Шаг 4.

Если , то выбрать цвет 0 (черный) и идти на Шаг 4.

Если , вернуться на Шаг 2.

Шаг 4:

Приписать цвет k точке экрана и перейти к следующей точке, начиная с Шаг 1.

program J2;

uses Graph, Crt;

type

TComplex = record

X : Real;

Y : Real;

end;

const

iter = 50;

max = 16;

x0=-0.9;

xn=0.9;

y0=-1.1;

yn=1.0;

var

z, t, c : TComplex;

n : Integer;

Cancel : Boolean;

gd, gm : Integer;

msx,msy : Real;

x, y :Real;

xc, yc : Integer;

begin

Cancel := false;

Randomize;

gd := Detect;

InitGraph(gd,gm,'c:\bp\bgi');

xc:=GetMaxX div 2;

yc:=GetMaxY div 2;

msx:= xc/xn;

msy:= yc/yn;

y:=y0;

while y<=yn do

begin

x:=x0;

while x<=xn do

begin

n := 0;

z.x := x*msx * 0.005;

z.y := y*msy * 0.005;

c.x := 0.11;

c.y := -0.66;

while (sqr(z.x) + sqr(z.y) < max) and (n < iter) do

begin

t := z;

z.x := sqr(t.x) - sqr(t.y) + c.x;

z.y := 2*t.x*t.y + c.y;

Inc(n);

if keypressed then

cancel := true;

end;

if n < iter then

begin

PutPixel(xc+round(x*msx),yc+round(y*msy),16 - (n mod 16));

end;

if cancel then

exit;

x:=x+0.002;

end;

y:=y+0.002;

end;

Readkey;

end.

Задание 2

Реализовать программу, строящую двумерное изображение заданной фигуры. Необходимо выполнить 2D преобразования и отобразить новое положение фигуры.

В таблице 2 каждому номеру варианта (№) соответствует фигура для построения

---

, и вид двумерного преобразования. Координаты вершин объектов сцены задаются самостоятельно.

6

Растяжение вдоль оси Y и поворот на 45° относительно начала координат

program kontrgraf;

uses crt,graph;

var dr,m:integer;

x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x22,x33,x44,x55,x66,x77,x88,x99,x1010:integer;

y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11,y22,y33,y44,y55,y66,y77,y88,y99,y1010:integer;

pressedkey:char;

label 1;

begin

x1:=100; x2:=200; x3:=250; x4:=200; x5:=100;

x6:=50; x7:=150; x8:=200; x9:=150; x10:=100;

y1:=250; y2:=250; y3:=350; y4:=450;

y5:=450; y6:=350; y7:=300; y8:=350; y9:=400; y10:=350;

dr:=Detect;

InitGraph(dr,m,'');

SetColor(5);

Line(50,50,640,50);

Line(50,50,50,480);

SetColor(14);

Line (x1,y1,x2,y2); {1-2}

Line (x2,y2,x3,y3); {2-3}

Line (x3,y3,x4,y4); {3-4}

Line (x4,y4,x5,y5); {4-5}

Line (x5,y5,x6,y6); {5-6}

Line (x6,y6,x1,y1); {6-1}

Line (x7,y7,x8,y8); {7-8}

Line (x8,y8,x9,y9); {8-9}

Line (x9,y9,x10,y10); {9-10}

Line (x10,y10,x7,y7); {10-7}

outtextxy(10,2,'Dlya preobrazovania figuri najmite klavishu Enter, Esc - vihod');

pressedkey:=readkey;

if pressedkey=chr(27) then halt;

if ord(pressedkey)=13 then goto 1;

1:

SetColor(20);

x11:=round(cos(pi/4)*x1+sin(pi/4)*y1);

y11:=round(-sin(pi/4)*x1+cos(pi/4)*y1);

x22:=round(cos(pi/4)*x2+sin(pi/4)*y2);

y22:=round(-sin(pi/4)*x2+cos(pi/4)*y2);

x33:=round(cos(pi/4)*x3+sin(pi/4)*y3);

y33:=round(-sin(pi/4)*x3+cos(pi/4)*y3);

x44:=round(cos(pi/4)*x4+sin(pi/4)*y4);

y44:=round(-sin(pi/4)*x4+cos(pi/4)*y4);

x55:=round(cos(pi/4)*x5+sin(pi/4)*y5);

y55:=round(-sin(pi/4)*x5+cos(pi/4)*y5);

x66:=round(cos(pi/4)*x6+sin(pi/4)*y6);

y66:=round(-sin(pi/4)*x6+cos(pi/4)*y6);

x77:=round(cos(pi/4)*x7+sin(pi/4)*y7);

y77:=round(-sin(pi/4)*x7+cos(pi/4)*y7);

x88:=round(cos(pi/4)*x8+sin(pi/4)*y8);

y88:=round(-sin(pi/4)*x8+cos(pi/4)*y8);

x99:=round(cos(pi/4)*x9+sin(pi/4)*y9);

y99:=round(-sin(pi/4)*x9+cos(pi/4)*y9);

x1010:=round(cos(pi/4)*x10+sin(pi/4)*y10);

y1010:=round(-sin(pi/4)*x10+cos(pi/4)*y10);

Line (x11,y11*2,x22,y22*2); {1-2}

Line (x22,y22*2,x33,y33*2); {2-3}

Line (x33,y33*2,x44,y44*2); {3-4}

Line (x44,y44*2,x55,y55*2); {4-5}

Line (x55,y55*2,x66,y66*2); {5-6}

Line (x66,y66*2,x11,y11*2); {6-1}

Line (x77,y77*2,x88,y88*2); {7-8}

Line (x88,y88*2,x99,y99*2); {8-9}

Line (x99,y99*2,x1010,y1010*2); {9-10}

Line (x1010,y1010*2,x77,y77*2); {10-7}

pressedkey:=readkey;

if pressedkey=chr(27) then halt;

closegraph;

end.

Заключение
Мною освоено:

• 
  Язык программирования Pascal. Работа с графикой в нем.
  
• 
  Алгоритмизация и построение программ.
  
• 
  Дисциплина «Компьютерная графика».
  

Благодаря понятным методическим указаниям, удалось научиться способам графического представления тех или иных действий с телами, понять связь матриц преобразования с этими действиями, а также как решить ту или иную задачу, составив сначала алгоритм, а затем по нему и программу на языке программирования, получить представление об основных приемах графического изображения тел. Кроме того, удалось научиться представлять данные с помощью MS Office, достаточно наглядно и быстро.

---

Смотрите также файлы

• К. Б. Малых москва 2023 п вопросы Выпишите какие методы исследования сенсорных систем вы знаете.docx

• Дуэль в жизни творчестве А. С. Пушкина.docx

• Ознакомление дошкольников с профессиями взрослых посредством реализации технологии Гость группы.docx

• Памятка о правилах проведения гвэ в 2023 году.pdf

• Дисциплина Осложненные условия разработки и эксплуатации нефтяных месторождений Задание 4 Расчет оптимального дебита и длины трещины для предотвращения выноса пропанта после грп.pdf