Министерство науки и высшего образования Российской Федерации

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Институт судостроения и морской арктической техники (Севмашвтуз)

(наименование высшей школы/ филиала/ института/ колледжа)

КОНТРОЛЬНАЯ РАБОТА

По дисциплине: Физика

На тему: Молекулярная физика и термодинамика

_________________________________________________________________________

Выполнила обучающаяся:

Кудрявцева София Сергеевна

(ФИО)

Направление подготовки / специальность:

15.03.05 Конструкторско-технологическое

обеспечение машиностроительных производств

(код и наименование)

Курс: 1

Группа: 523227

Руководитель:

Шмонина Светлана Алексеевна

(ФИО руководителя)

Отметка о зачете

(отметка прописью)

(дата)

Руководитель

С. А. Шмонина

(подпись руководителя)

(инициалы, фамилия)

Северодвинск 2023

---

ЛИСТ ДЛЯ ЗАМЕЧАНИЙ

Контрольная работа №2

2.07. Сосуд емкостью 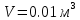содержит азот массой 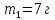и водород массой 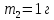при температуре 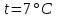. Определить давление 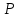смеси газов.

Дано:















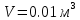
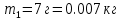
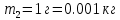
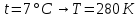
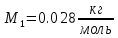
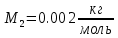
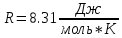
Найти:



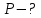
Решение:

Воспользуемся законом Менделеева-Клапейрона:

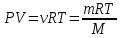(1)

По закону Дальтона давление смеси будет равно сумме парциальных давлений:

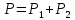(2)

Выразим через (1) формулу давление для каждого газа:





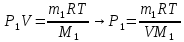
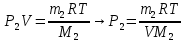
Подставим теперь это всё в нашу (2) формулу:





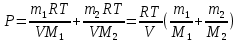
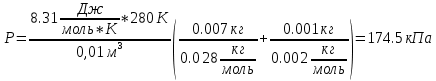
Ответ:

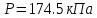
2.17. Определить среднее значение 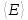полной кинетической энергии одной молекулы гелия, кислорода и водяного пара при температуре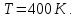

Дано:

---

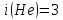
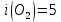
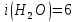
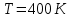
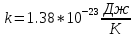
Найти:



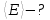
Решение:

Полная кинетическая энергия молекул газа:



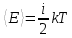
Подставим в данную формулу степени свободы для каждого газа.

Для гелия:





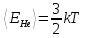
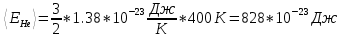
Для кислорода:




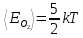
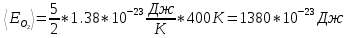
Для водяного пара:





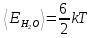
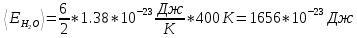
Ответ:



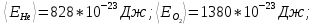
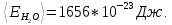
2.27. На какой высоте 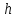над поверхностью Земли плотность воздуха в 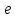раз (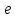 - основание натуральных логарифмов) меньше по сравнению с его плотностью 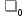на уровне моря? Температуру 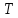воздуха, равную 273 К, и ускорение 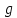свободного падения считать независящими от высоты.

Дано:











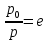
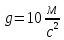
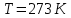
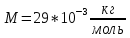
Найти:



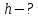
Решение:

Запишем закон Менделеева-Клайперона:



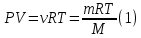
Заметим, что плотность воздуха, можно выразить через:

---

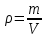
То подставив эту формулу в (1):





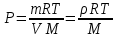
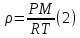
Теперь мы видим связь между плотностью и давлением по мере увеличения высоты, меняются они вместе, а значит по уравнению Больцмана для плотности воздуха:



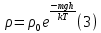
Где масса молекул воздуха:





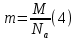
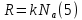
Теперь подставим уравнение (4) и (5) в (3):





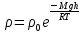
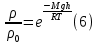
Из дано известно соотношение плотностей воздуха на поверхности и над уровнем моря, тогда учитывая 6 формулу, получим:







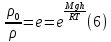
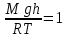
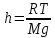
Подставим значения в формулу:



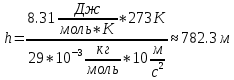
Ответ:

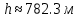
2.37. Баллон емкостью 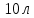содержит 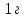водорода. Определить среднюю длину свободного пробега молекул. Диаметр молекул водорода равен .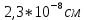

Дано:











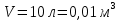
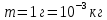
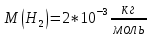
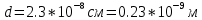
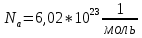
Найти:



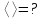
Решение:

Средняя длина свободного пробега молекул:



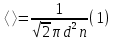
Концентрация молекул:

---

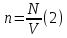
Количества вещества:



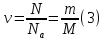
Теперь объединив две формулы (2) и (3), получим:




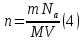
Теперь, подставив в (1) уравнение (4), получим:



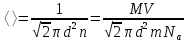
Подставим значения в уравнение и найдём среднюю длину свободного пробега молекул:



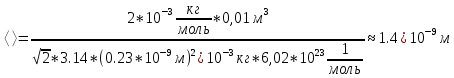
Ответ:

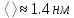
2.47. Определить удельные теплоемкост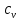и и 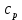, если известно, что некоторый газ при нормальных условиях имеет удельный объем (отношение объема газа к его массе) 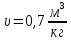. Что это за газ?

Дано:









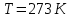
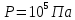
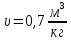
Найти:





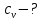
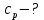
Решение:

Напишем уравнение удельного объёма:



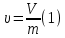
Напишем уравнение Менделеева-Клайперона:



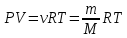
Выразим молярную массу вещества:



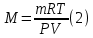
Подставим уравнение (1) в (2):





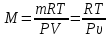
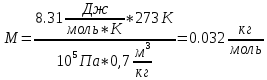
Данную малярную массу имеет кислород. А значит газ двухатомный. Число степеней свободы, равно:

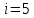
Для двухатомного вещества удельная теплоёмкость:





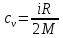
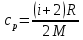
Подставим значения:

---

Смотрите также файлы

• Решение Товарная продукция представляет собой сумму.docx

• Уравнение Шредингера. Собственные функции и собственные значения.docx

• Bадреноблокаторы Сингх Рана Мадхурипу.pptx

• Реферат на тему "закономерности развития биосферы" содержание эволюция биосферы.docx

• Таырыбы Ктілетін нтижелер.docx