Файл: Научноисследовательская работа по математике Математика в школе. Проценты, дроби, доли в кулинарии. Илиева Х. М. 5 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 108
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
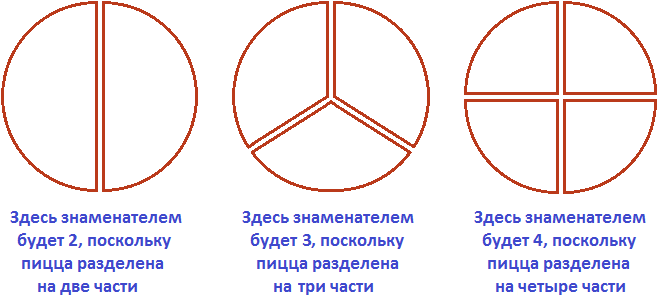
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли
С помощью переменных дробь можно записать так:
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
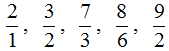 Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.Теперь возьмём к примеру неправильную дробь
и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
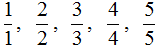
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь
Допустим, мы хотим съесть
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь
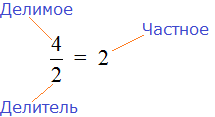
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
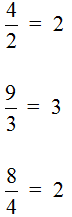
1.5 Измерения в кулинарии
Математика в кулинарии имеет большое значение, так как для приготовления любого блюда должен соблюдаться рецепт. В рецепте указывается точное соотношение продуктов, которое необходимо соблюдать в процессе приготовления. При взвешивании продуктов в кулинарии используются математические величины масса и объём. Ими тоже необходимо уметь пользоваться. Единицы времени играют далеко не последнюю роль в приготовлении блюд. Приготовленные блюда нужно умело делить на порции, в чём нам опять же поможет математика.
Вес - можно измерить столовой или чайной ложкой
Объём - жидкости можно измерить специальным мерным стаканом
Время – все блюда готовятся по времени
Температура – каждое блюдо готовится при своей температуре
-
Практическая часть
2.1 Практическая значимость
Чтобы ответить на поставленные вопросы, мы поговорили с мамой и выяснили, что для того чтобы пользоваться кулинарными рецептами и производить перерасчёт продуктов по ним, требуется знать, что такое отношение, пропорциональность.
В процессе работы мы сталкиваемся с необходимостью определения пропорции неких ингредиентов, которые нам нужны, относительно количества используемой муки. Эта пропорция называется пекарский процент или процент пекаря.
Вы наверняка слышали, что выпечка — это точная наука. Чтобы добиться желаемого результата — будь то блины, пышные булочки или торт — вы должны точно отмерять ингредиенты. Один из способов реализовать идеальный рецепт — использовать процентную формулу пекаря- пекарский процент!
Что такое пекарский процент?
Пекарский процент (также известный как математика пекаря) — это метод определения пропорции ингредиентов при выпечке по отношению к весу муки. Мы можем использовать процент пекаря по многим причинам, в том числе:
-
Для вычисления точных пропорций ингредиентов с одной единицей измерения; -
Для масштабирование рецептов в большую или меньшую сторону без изменения консистенции теста или кляра; или -
Для экспериментов с ингредиентами, или для изменений только одного из них, сохраняя процентное содержание других ингредиентов постоянным.
Что такое процентная формула пекаря?
Теперь вы, вероятно, задаетесь вопросом, как рассчитать формулу пекарского процента. Не волнуйтесь, Формула процента пекаря довольно проста:
Процент пекаря = (вес ингредиента / общий вес муки) × 100%
Как рассчитать пекарский процент на примере?
Чтобы разобрать формулу на примере, т.к. сейчас для всех мусульман наступил священный месяц Рамадан, и все женщины бывают заняты приготовлением блюд на сухур и на ифтар, я тоже никогда не остаюсь в стороне. Т.к. я единственная дочка в семье и у меня еще три брата мне всегда приходится помогать маме по кухне. В каждой семье на сухур готовят курузную лепешку – чурек, т.к. чурек не дает чувствовать голод и легче держать уразу. Для закрепления своей темы эту миссию на сегодня я решила взять на себя.
Рецепт чурека: Кукурузная мука 600г., сахар 1ч.л., соль 1 ч.л., сода 1 ч.л., растительное масло 3 ст.л., 2 яйца, кефир 1 л.
Важно запомнить, что в пекарских расчетах все считается от муки и мука принимается за 100%. Остальные ингредиенты считаются в процентах от муки.
Для приготовления чурека мне нужно:
600г. кукурузной муки = 100%
1л. Кефира примерно 1000г = 166%
1ч.л. соды =10г. = 1.7%
1ч.л. соли=10г = 1.7%
1ч.л. сахара=10г = 1.7%
3 столовые ложки растительного масла=60г =10%
2 яйца=100г=17%
Общая масса ингредиентов =1790г.=298.1%
Соответственно масса теста равна1790 гр. , а процентное соотношение всех инградиентов равно 298.1%. Как вы видите суммарные доли всех ингредиентов будут больше 100%.
В профессиональных рецептах очень часто не указывается состав в граммах, но все инградиенты выражены в процентах и рецептура выглядит так:
Кефир = 160%
сода = 1.7%
соль= 1.7%
сахар = 1.7%
растительное масло =10%
яйца=17%
кукурузная мука = 100%
Важно запомнить еще один секрет ! – Если разделить вес теста в граммах на суммарный процент инградиентов то вы получите вес муки в граммах.
Например в нашем случае вес теста 1790гр. , а суммарный процент инградиентов 298% или 2.98. Делим 1790гр на 2.98 и получаем 600гр муки.

 Если наш чурек разделим по диагонали на две равные части, то мы получим две равные доли и тогда каждая доля будет равна ½ или 50%
Если наш чурек разделим по диагонали на две равные части, то мы получим две равные доли и тогда каждая доля будет равна ½ или 50%Если же чурек разделить на 4 части, то каждая доля будет равна ¼ чурека или 25%
Заключение
Изучив тему «Математика в школе. Проценты, дроби, доли в кулинарии», я ответила на вопросы, которые поставила в начале проекта.