ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторна робота 4.1.
Розробка програми швидкого дискретного потенціювання (ШДП) для виконання обчислювальних операцій в алгоритмі шифрування RSA.
Лістинг програмного коду виконання завдання:
using System;
using System.IO;
using System.Numerics;
namespace LargeNumbersCalculator
{
class Adder
{
private static Random random = new Random();
private const int MinNumberOfDigits = 1000;
private const int MaxNumberOfDigits = 10000;
public static string SumValuesFromFiles(String path)
{
string[] lines = File.ReadAllLines(path);
BigInteger firstNumber = BigInteger.Parse(lines[0]);
BigInteger secondNumber = BigInteger.Parse(lines[1]);
Console.WriteLine("\nПерше довге числ:\n");
Console.WriteLine(firstNumber);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondNumber);
return (firstNumber + secondNumber).ToString();
}
public static string SumValuesFromFiles2(String path)
{
string[] lines = File.ReadAllLines(path);
BigInteger firstNumber = BigInteger.Parse(lines[0]);
BigInteger secondNumber = BigInteger.Parse(lines[1]);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstNumber);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondNumber);
return (firstNumber - secondNumber).ToString();
}
public static string SumValuesFromFiles3(String path)
{
string[] lines = File.ReadAllLines(path);
BigInteger firstNumber = BigInteger.Parse(lines[0]);
BigInteger secondNumber = BigInteger.Parse(lines[1]);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstNumber);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondNumber);
return (firstNumber * secondNumber).ToString();
}
public static string SumValuesFromFiles4(String path)
{
string[] lines = File.ReadAllLines(path);
BigInteger firstNumber = BigInteger.Parse(lines[0]);
BigInteger secondNumber = BigInteger.Parse(lines[1]);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstNumber);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondNumber);
return (firstNumber / secondNumber).ToString();
}
public static string SumGeneratedValues()
{
string firstString = GenerateLongValue();
string secondString = GenerateLongValue();
BigInteger firstNumber = BigInteger.Parse(firstString);
BigInteger secondNumber = BigInteger.Parse(secondString);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstString);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondString);
return (firstNumber + secondNumber).ToString();
}
public static string GenerateLongValue()
{
int numberOfDigits = random.Next(MinNumberOfDigits, MaxNumberOfDigits);
string generatedNumber = "";
for (int i = 0; i < numberOfDigits; i++)
{
generatedNumber += GenerateDigit();
}
return generatedNumber;
}
public static string SumGeneratedValues2()
{
string firstString = GenerateLongValue();
string secondString = GenerateLongValue();
BigInteger firstNumber = BigInteger.Parse(firstString);
BigInteger secondNumber = BigInteger.Parse(secondString);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstString);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondString);
return (firstNumber - secondNumber).ToString();
}
public static string SumGeneratedValues3()
{
string firstString = GenerateLongValue();
string secondString = GenerateLongValue();
BigInteger firstNumber = BigInteger.Parse(firstString);
BigInteger secondNumber = BigInteger.Parse(secondString);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstString);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondString);
return (firstNumber * secondNumber).ToString();
}
public static string SumGeneratedValues4()
{
string firstString = GenerateLongValue();
string secondString = GenerateLongValue();
BigInteger firstNumber = BigInteger.Parse(firstString);
Console.WriteLine("\nДовге число:\n");
Console.WriteLine(firstString);
return (firstNumber * firstNumber).ToString();
}
public static string SumGeneratedValues5()
{
string firstString = GenerateLongValue();
string secondString = GenerateLongValue();
BigInteger firstNumber = BigInteger.Parse(firstString);
BigInteger secondNumber = BigInteger.Parse(secondString);
Console.WriteLine("\nПерше довге число:\n");
Console.WriteLine(firstString);
Console.WriteLine("\nДруге довге число:\n");
Console.WriteLine(secondString);
return (firstNumber % secondNumber).ToString();
}
public static string GenerateDigit()
{
return random.Next(0, 10).ToString();
}
}
}
using System;
using System.IO;
namespace LargeNumbersCalculator
{
class Program
{
static void Main(string[] args)
{
//Console.WriteLine("\nSUMA:\n" + Adder.SumGeneratedValues());
Console.WriteLine("\nСУМА:\n" + Adder.SumValuesFromFiles(Path.Combine(Environment.CurrentDirectory, "числа.txt")));
Console.ReadKey();
Console.WriteLine("\nРIЗНИЦЯ:\n" + Adder.SumGeneratedValues2());
Console.ReadKey();
Console.WriteLine("\nДОБУТОК:\n" + Adder.SumGeneratedValues3());
Console.ReadKey();
Console.WriteLine("\nКВАДРАТ:\n" + Adder.SumGeneratedValues4());
Console.ReadKey();
Console.WriteLine("\nЗАЛИШКИ ПО МОДУЛЮ ДІЛЕННЯ ДВОХ ЧИСЕЛ:\n" + Adder.SumGeneratedValues5());
Console.ReadKey();
}
}
}
Результат запуску програми на виконання:
Лабораторна робота 4.2.
Розробка програми генератора великих простих чисел (ВПЧ).
Метод решета числового поля (як спеціальний, і загальний) можна як удосконалення найпростішого методу — методу раціонального решета, чи методу квадратичного решета. Подібні до них алгоритми вимагають знаходження гладких чисел порядку
. Розмір цих чисел експоненційно зростає із зростанням
. Метод решета числового поля, у свою чергу, вимагає знаходження гладких чисел субекспоненційного щодо розміру. Завдяки тому, що ці числа менші, ймовірність того, що число такого розміру виявиться гладким вище, що є причиною ефективності методу решета числового поля. Досягнення прискорення обчислень у межах методу проводять у числових полях, що ускладнює алгоритм, проти більш простим раціональним решетом.Основні принципи
-
Метод факторизації Ферма для факторизації натуральних непарних чисел n, що полягає у пошуку таких цілих чисел x та y, що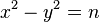
, що веде до розкладання
. -
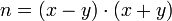Знаходження підмножини множини цілих чисел, добуток яких — квадрат -
Складання факторної бази: набору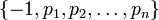
де pi — прості числа такі, що
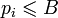для деякого B. -
Просіювання виконується подібно до решету Ератосфена (звідки метод і отримав свою назву). Решетом служать найпростіші числа факторної бази та їх ступеня. При просіюванні число не «викреслюються», а поділяється на число із решета. Якщо в результаті число виявилося одиницею, воно B-гладке. -
Основна ідея полягає в тому, щоб замість перебору чисел та перевірки, чи діляться їх квадрати по модулю n на прості числа з факторної бази, перебираються прості числа з бази та одразу для всіх чисел виду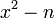
перевіряється, чи діляться вони це просте число чи його ступінь.
Обчислювальну складність алгоритмів модулярного експонентування за її реалізації різних обчислювальних платформах зазвичай оціните кількістю використаних них операцій процесорного множення. Процесорними називають цілі операції, що виконуються над k-розрядними числами, довжина яких відповідає розрядності процесора.
Процес модулярного експоненцування зводиться до послідовного виконання log2E = n циклів, у кожному з яких виконується операція зведення в квадрат результату операції попереднього циклу і в залежності від поточного біта ступеня E виконується операція множення. Залежно від порядку, в якому аналізуються розряди ступеня E, можна розглянути 2 типи алгоритмів експоненцювання:
1) алгоритми, що передбачають аналіз розрядів ступеня Е, починаючи зі старших розрядів (зліва направо). У нотаціях мови програмування алгоритм цього може бути поданий як:
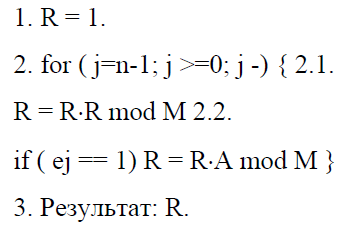
При цьому, під час кожної ітерації циклу виконується зведення числа квадрат і множення на постійне число, що дорівнює А, що створює потенційні передумови для підвищення швидкості множення.
Недоліком є те, що операції виконуються строго послідовно та належать критичному шляху. Не дозволяє реалізувати паралельне обчислення операцій.
2) Алгоритми, які передбачають аналіз розрядів ступеня Е починаючи з молодших (праворуч ліворуч). Алгоритм модулярного експонентування цього може бути представлений у вигляді:
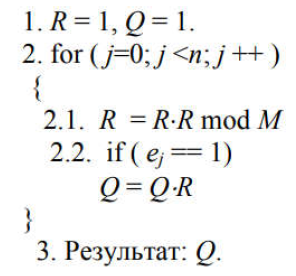
За такої реалізації алгоритму є потенційна можливість розпаралелити модульне експоненціювання. Аналіз зазначеного алгоритму показує, що базовими операціями виконання модулярного експонентування є зведення квадрат і модульне множення на фіксоване число, час виконання яких фактично визначається продуктивністю обчислення АЕ mod М.
Більшість алгоритмів модулярного експоненціювання для реалізації згаданих двох операцій використовують єдину операцію множення. У свою чергу, час виконання модулярного множення визначається двома складовими: час, який необхідний для реалізації власне множення та час, що витрачається на модульну редукцію. У класичному множенні модульні редукції реалізуються з використанням операції розподілу і, відповідно, друга складова відіграє значну роль. Значна ефективність обчислювальної реалізації модулярного множення досягається при використанні алгоритму Монтгомері, в якому модульна редукція зводиться до зсуву на k розрядів. Тому на практиці при виконанні медулярного експоненціювання в більшості використовується алгоритм RSA-Монтгомері.
Позначимо як Mont (A, B) множення Монтгомері, яке формує результат
R = A * B * U mod M,
де U модульна інверсія числа 2n по модулю M, тобто U = (2n) -1mod M.
Алгоритм модулярного експонентування Монтгомері можна представити з використання введених нотацій таким чином:
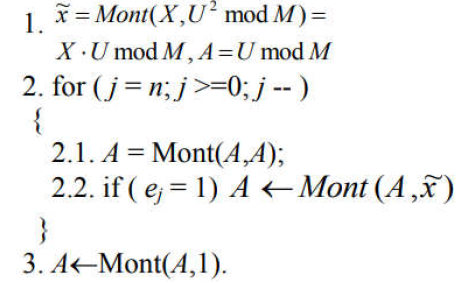
Лістинг програмного коду виконання завдання:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Collections;
using System.Threading;
namespace Prime_Numbers
{
public partial class Form1 : Form
{
bool working = false;
int minN = 0;
int maxN = 0;
public Form1()
{
InitializeComponent();
}
public static bool IsPrime(int n)
{
if (n > 1)
{
return Enumerable.Range(1, n).Where(x => n % x == 0).SequenceEqual(new[] { 1, n });
}
return false;
}
private void run_Click(object sender, EventArgs e)
{
if (!working) {
try
{
working = true;
maxN = int.Parse(maxNumber.Text);
minN = int.Parse(textBox1.Text);
results.Text = "";
progress.Maximum = maxN;
for (int i = minN; i <= maxN; i++)
{
Form1.ActiveForm.Update();
progress.Value = i;
if (IsPrime(i))
{
Console.WriteLine(i + " Просте число");
results.Text += i + "\r\n";
results.Update();
}
else
{
Console.WriteLine(i + " Не просте число");
}
}
working = false;
}
catch (Exception ex)
{
progress.Value = 0;
working = false;
}
}
}
private void label1_Click(object sender, EventArgs e)
{
}
}
}
Результат запуску програми на виконання:
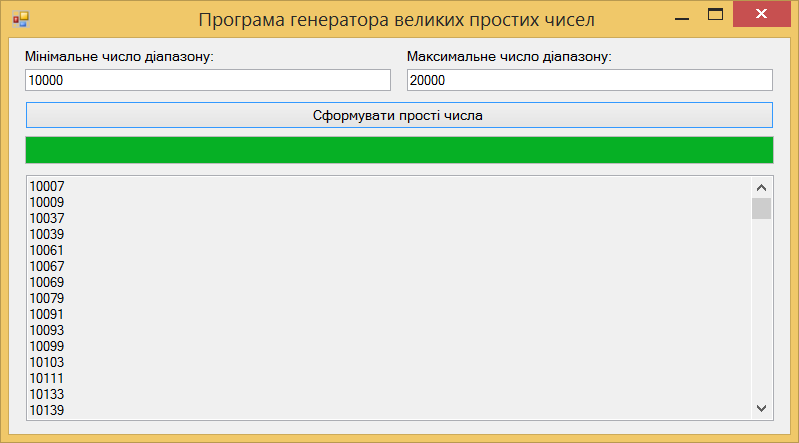
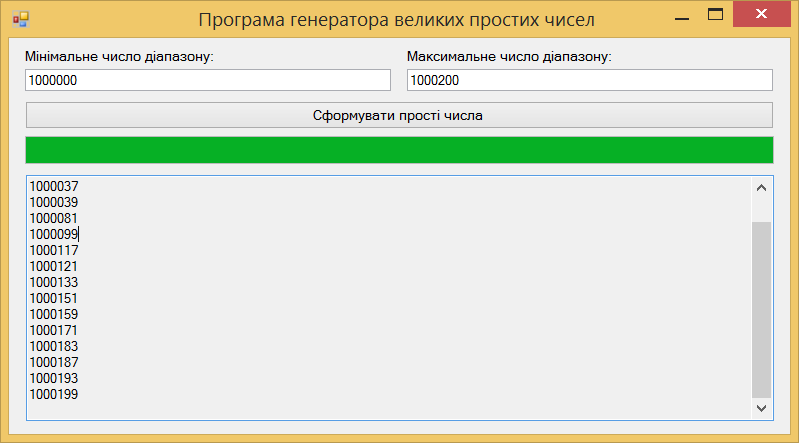
Лабораторна робота 5.
Розробка програми керування ключами шифрування за схемою RSA.
Дана реалізація криптосистеми складається з 4 основних класів:
-
BigNumberGenerator – генератор великих чисел, як простих і звичайних.
Для перевірки великої кількості на простоту було реалізовано імовірнісний тест Міллера-Рабіна.
Тест Міллера – Рабіна – ймовірнісний поліноміальний тест простоти. Він дозволяє ефективно визначати, чи є задане число складеним. Однак з його допомогою не можна довести простоту простоти числа. Коротка суть його алгоритму така для визначення простоти числа m нам необхідно знайти r свідків простоти, і якщо вони знайдені, то число з високою ймовірністю є простим, якщо не знайдені, то число явно складене. Число r рекомендується брати як
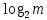
З теореми Рабіна випливає, що якщо r випадково вибраних чисел виявилися свідками простоти числа m, то ймовірність того, що m складне не перевищує
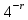. Також вона стверджує, що складне непарне число m має не більше різних свідків простоти, де – функція Ейлера