ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
RSAGenerator – генератор ключів RSA, що працює за викладеним вище алгоритмом генерації ключів. -
Core - ядро програми, у ньому закладено й інші основні необхідні методи. -
Converter – клас працюючий з користувачем, тобто. той самий клас, який перетворює ваш текст на шифр-текст і навпаки.
Час генерації ключів – випадкова величина, що з генерацією великого простого числа. Нижче наведено часовий інтервал генерації ключів на різних машинах.
10 тестів на ключ на машині Intel Pentium CPU B970 2.30 GHz з 6 Гб ОЗУ
-
64 bit – 0 секунд -
128 bit – від 0 до 2 секунд -
256 bit – від 0 секунд до 12 секунд -
512 bit – від 0 секунд до 3 хвилин 13 секунд -
1024 bit – від 58 секунд до 139 хвилин 35 секунд -
2048 bit - за 3 години не завершився навіть перший тест
10 тестів на ключ на машині Intel Core i7 CPU 860 2.8GHz з 4 Гб ОЗУ
-
64 bit – 0 секунд -
128 bit – від 0 до 2 секунд -
256 bit – від 0 до 6 хвилин 13 секунд -
512 bit – від 3 секунд до 3 хвилин 42 секунд -
1024 bit – від 34 секунд до 112 хвилин 35 секунд -
2048 bit - за 3 години не завершився навіть перший тест
Лістинг програмного коду виконання завдання:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Text;
using System.Windows.Forms;
using System.Security.Cryptography;
using System.IO;
using RSAEncryptionLib;
namespace RSAEncryptionTester
{
public partial class MainForm : Form
{
RSAEncryption myRsa = new RSAEncryption();
public MainForm()
{
InitializeComponent();
}
private void createKeyToolStripMenuItem_Click(object sender, EventArgs e)
{
RSACryptoServiceProvider rsa = new RSACryptoServiceProvider();
string privateKey = rsa.ToXmlString(true);
File.WriteAllText(Application.StartupPath + "\\PrivateKey.xml", privateKey);
string publicKey = rsa.ToXmlString(false);
File.WriteAllText(Application.StartupPath + "\\PublicKey.xml", publicKey);
MessageBox.Show("Ключ успешно создан по адресу:\n" + Application.StartupPath);
}
private void loadKeyToolStripMenuItem_Click(object sender, EventArgs e)
{
openKeyFileDialog.InitialDirectory = Application.StartupPath;
якщо (openKeyFileDialog.ShowDialog() != DialogResult.OK)
return;
// Визначити, який пункт меню LoadKey було вибрано (загальнодоступний чи приватний)
bool isLoadPrivate =
(sender as ToolStripMenuItem).Name == "loadPrivateKeyToolStripMenuItem" ? true : false;
try
{
if (isLoadPrivate)
myRsa.LoadPrivateFromXml(openKeyFileDialog.FileName); // Завантажуємо приватний ключ до користувацького екземпляру RSA
else
myRsa.LoadPublicFromXml(openKeyFileDialog.FileName); // Або публічний ключ
if (!chkShowData.Checked) // Чи хоче користувач бачити компоненти Key у формі?
return; // Гадаю, що ні
// Якщо хоче, то завантажуємо ключ в .NET RSA клас, щоб показати його компоненти у формі:
RSACryptoServiceProvider localRsa = new RSACryptoServiceProvider();
localRsa.FromXmlString(File.ReadAllText(openKeyFileDialog.FileName));
RSAPпараметри rsaParams = localRsa.ExportParameters(isLoadPrivate);
txtExponent.Text = GetHexString(rsaParams.Exponent);
txtModulus.Text = GetHexString(rsaParams.Modulus);
if (isLoadPrivate)
txtD.Text = GetHexString(rsaParams.D); // Цей параметр є тільки в приватному ключі
// Очищення екземпляру RSA
localRsa.Clear();
}
catch (Виключення ex)
{
MessageBox.Show("Помилка читання ключа,\nMessage: " + ex.Message);
}
}
private void EncryptionToolStripMenuItem_Click(object sender, EventArgs e)
{
// Визначити, який пункт меню Шифрування було вибрано (загальнодоступний чи приватний)
bool isEncryptPrivate =
(sender as ToolStripMenuItem).Name == "privateEncryptionToolStripMenuItem" ? true : false;
// Перевірити, чи в клас rsa завантажено правильний ключ
if (isEncryptPrivate && !myRsa.IsPrivateKeyLoaded)
{
MessageBox.Show("Завантажте закритий ключ перед кодуванням.");
return;
}
else if(!isEncryptPrivate && !myRsa.IsPublicKeyLoaded)
{
MessageBox.Show("Завантажте відкритий ключ перед кодуванням.");
return;
}
try
{
byte[] message = Encoding.UTF8.GetBytes(txtMessage.Text);
byte[] encMessage = null;
if (isEncryptPrivate) // Виклик потрібного методу шифрування згідно з вибором користувача
encMessage = myRsa.PrivateEncryption(message);
else
encMessage = myRsa.PublicEncryption(message);
txtEncMsg.Text = Convert.ToBase64String(encMessage);
}
catch (Виключення ex)
{
MessageBox.Show("Помилка читання закодованих даних,\nMessage: " + ex.Message);
}
}
private void DecryptionToolStripMenuItem_Click(object sender, EventArgs e)
{
// Визначити, який пункт меню Decryption було вибрано (загальнодоступний чи приватний)
bool isDecryptPrivate =
(sender as ToolStripMenuItem).Name == "privateDecryptionToolStripMenuItem" ? true : false;
// Перевірити, чи в клас rsa завантажено правильний ключ
if (isDecryptPrivate && !myRsa.IsPrivateKeyLoaded)
{
MessageBox.Show("Завантажте закритий ключ перед дешифруванням.");
return;
}
else if(!isDecryptPrivate && !myRsa.IsPublicKeyLoaded)
{
MessageBox.Show("Завантажте відкритий ключ перед дешифруванням.");
return;
}
try.
{
byte[] decMessage = Convert.FromBase64String(txtEncMsg.Text);
byte[] message = null;
if (isDecryptPrivate) // Виклик потрібного методу розшифрування згідно з вибором користувача
message = myRsa.PrivateDecryption(decMessage);
else
message = myRsa.PublicDecryption(decMessage);
рядок sMsg = Encoding.UTF8.GetString(message);
MessageBox.Show("Повідомлення декодування:\n" + sMsg);
}
catch ((Exception ex)
{
MessageBox.Show("Помилка читання декодованих даних,\nMessage: " + ex.Message);
}
}
private string GetHexString(byte[] byteArray)
{
Конструктор рядків hexString = new StringBuilder(byteArray.Length * 2);
for (int i = 0; i < byteArray.Length; i++)
hexString.Append(string.Format("{0:X}", byteArray[i]));
int x = hexString.Capacity;
return hexString.ToString();
}
private void MainForm_FormClosing(object sender, FormClosingEventArgs e)
{
myRsa.Dispose();
}
private void txtExponent_TextChanged(object sender, EventArgs e)
{
}
}
}
Першим етапом є відкриття файлу rk.xtq з процесом та вказівки параметрів відображення. Ці налаштування виконуються після натискання кнопки OK. До кожного процесу передбачено виведення інформації про деталі шифрації-дешифрації.
Робота з програмою починається після запуску файлу rsa.exe на виконання. На екрані з'являється головна форма управління програмою (рис.5.1)
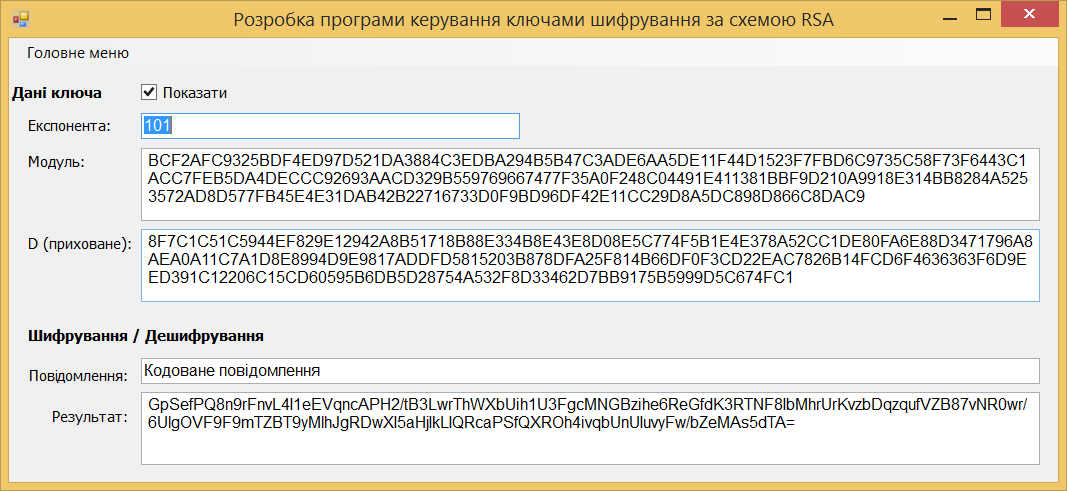
Рис. 5.1. Головне вікно програми, режим формування та завантаження ключів
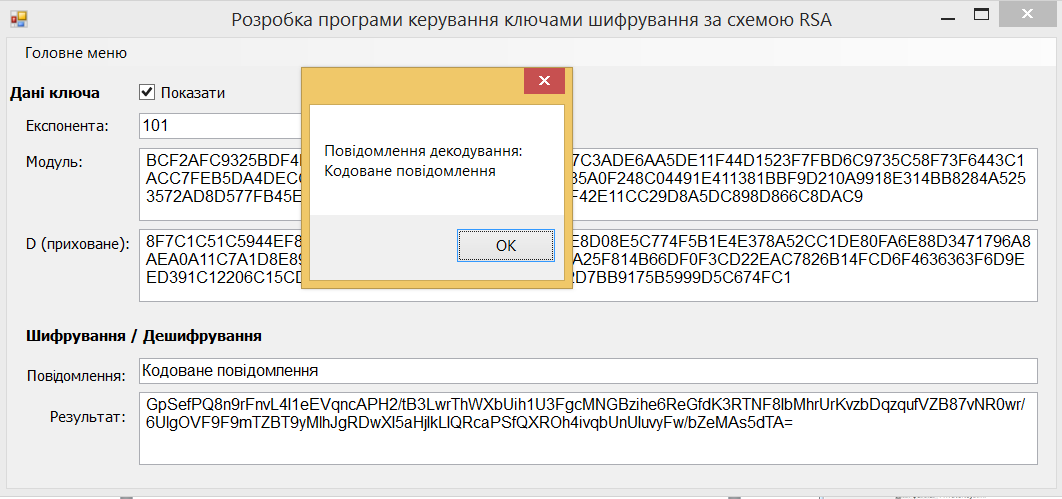
Рис. 5.2. Результат кодування
Для переходу в режими роботи в головному меню представлені варіанти завантаження відкритих, закритих ключів, виконання шифрації-дешифрації з використанням відповідних ключів.
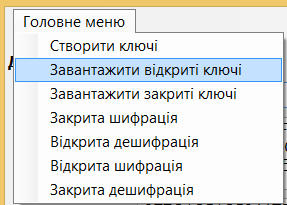
Рис. 5.3. Головне меню програми
Для початку роботи виконується завантаження ключів після вибору пункту «Завантажити відкриті ключі», вказавши найменування файлу з даними ключа:
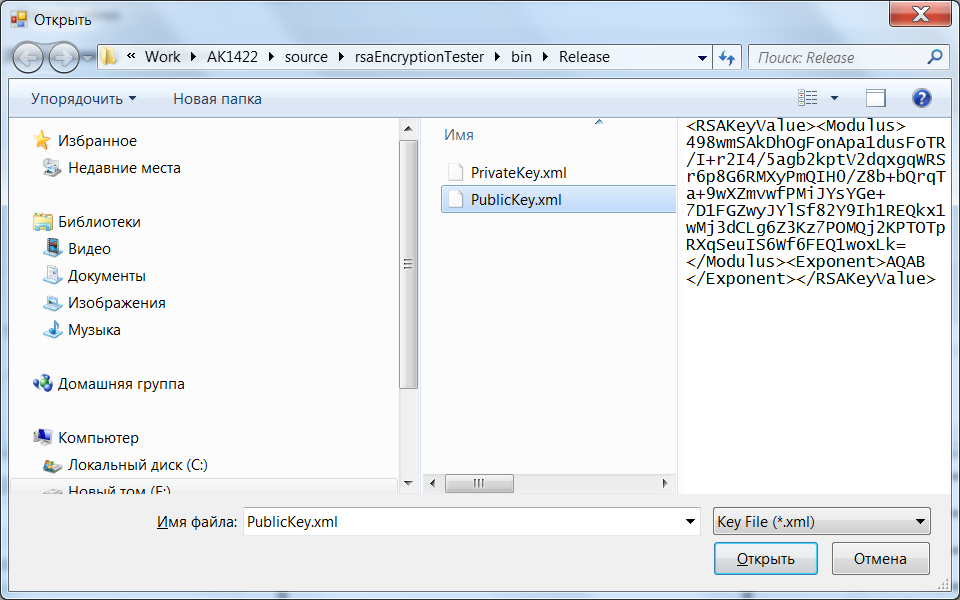
Рис. 5.4. Вибір відкритого ключа
Для початку роботи виконується завантаження ключів після вибору пункту «Завантажити закриті ключі», вказавши найменування файлу з даними ключа PrivateKey.xml:
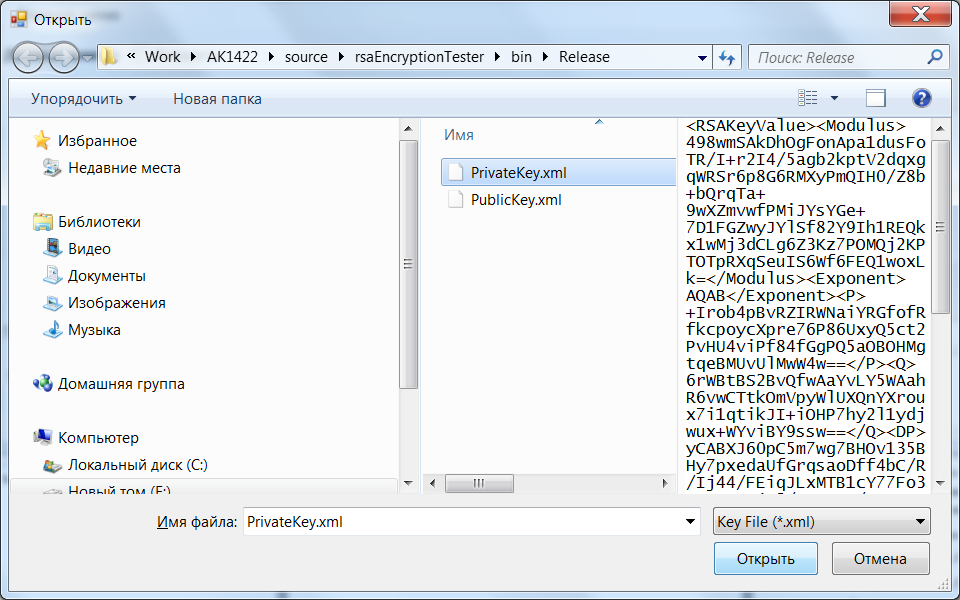
Рис. 5.5. Вибір закритого ключа
Далі в текстове поле «Текст повідомлення» слід ввести текст, що кодується. Після цього з меню вибирається варіант шифрації – відкрита чи закрита.
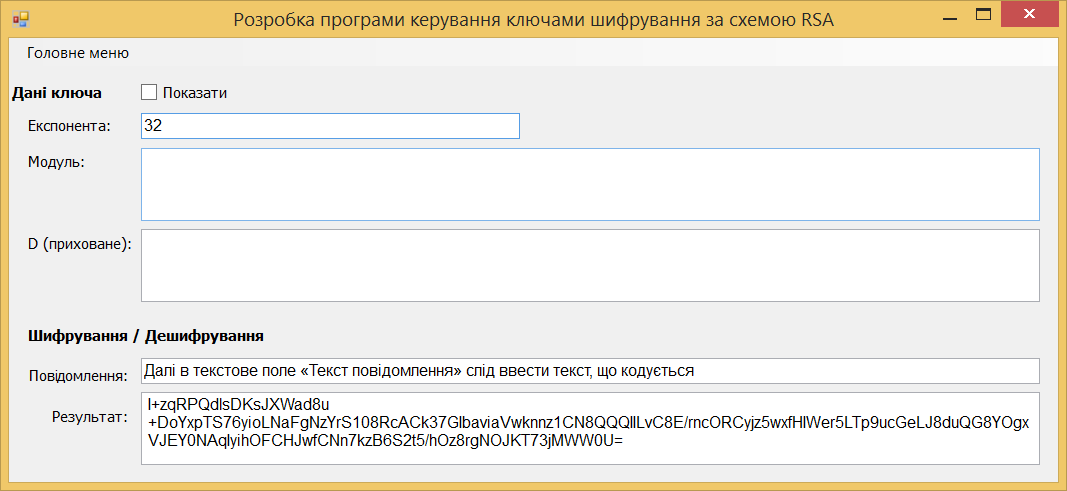
Рис. 5.6. Результат відкритого кодування
При закритій системі результат шифрування коригується автоматично і з'являється у нижній частині вікна:
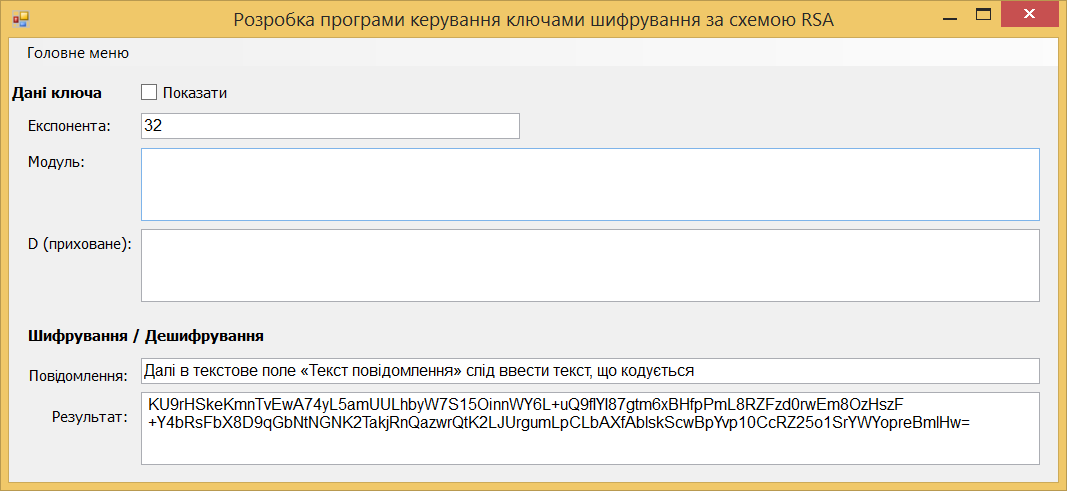
Рис. 5.7. Результат закритого кодування
При помилці кодування при використанні неправильного ключа декодований текст має такий вигляд:
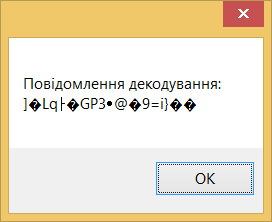
Рис. 5.8. Результат помилкового декодування
- результат створення відкритих та закритих ключів:
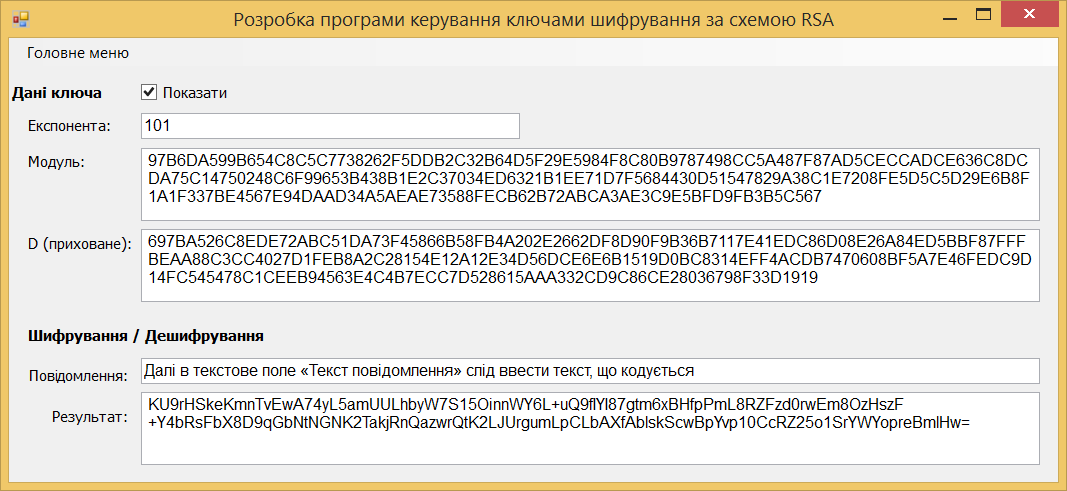
Рис. 5.9. Результат створення ключів та кодування
Лабораторна робота 6.
Розробка програми формування сигнатури повідомлення (цифровий підпис) на основі симетричного алгоритму шифрування. Програма реалізує два режими роботи: просте поблокове шифрування і дешифрування повідомлень (режим електронної кодової книги), а також зчеплення блоків шифру при формуванні цифрового підпису.
Ефективними системами криптографічного захисту є асиметричні криптосистеми, звані також криптосистемами з відкритим ключем. У таких системах для шифрування даних використовується один ключ, а для дешифруванняінший ключ (звідси і назваасиметричні). Перший ключ є відкритим і може бути опублікований для всіх користувачів системи, які бажають зашифровувати дані. Неможливо дешифрувати дані за допомогою відкритого ключа.
Для дешифрування даних використовує другий ключ, секретний. Зрозуміло, що ключ дешифрування не може бути визначений з відкритого ключа шифрування. Узагальнену схему асиметричної криптосистеми з відкритим ключем показано на рис. 6.1.
| Схема асиметричної криптосистеми  Рис. 6.1. Схема асиметричної криптосистеми |
У цій криптосистемі застосовують два різні ключі: KB - відкритий ключ одержувача; kB - секретний ключ одержувача У. Значення ключів KB і kB залежить від початкового стану генератора ключів, вибираного випадковим чином. Розкриття секретного ключа kB за відомим відкритим ключем KB має бути обчислювально-нерозв'язною задачею, тобто. вимагати досить тривалого часу.
Характерні особливості асиметричних криптосистем:
-
Відкритий ключ KB і криптограма можуть бути відправлені незахищеними каналами, тобто. противнику відомі KB та С. -
Алгоритми шифрування (далі EK) та дешифрування (далі Dk) є відкритими. -
Захист інформації в асиметричній криптосистемі ґрунтується на секретності ключа kB.
У. Діффі та М. Хеллман сформулювали вимоги, виконання яких забезпечує безпеку асиметричної криптосистеми:
-
Обчислення пари ключів (KB, kB) одержувачем на основі початкової умови має бути простим. -
Відправник А, знаючи відкритий ключ KB і повідомлення М може легко обчислити криптограму С = EK (M). -
Одержувач В, використовуючи секретний ключ kB та криптограму
Зможе легко відновити вихідне повідомлення M = Dk (С). -
Противник, знаючи відкритий ключ KB, намагаючись обчислити секретний ключ kB наштовхується на непереборну обчислювальну проблему.
Оскільки прості числа повинні вибиратися таким чином, щоб факторизувати їхній добуток було обчислювально неможливо, рекомендується брати їх дуже великими і однаковою довжиною. Так, N довжини 1024 біта P і Q повинні бути довжиною приблизно 512 біт.
Різниця чисел P та Q також не повинна бути маленькою, оскільки в цьому випадку PQ і, отже, P!Синтаксична помилка, N. Таким чином, розкладання N може бути знайдено простим розподілом на всі числа порядку!Синтаксична помилка, N.
Числа P і Q повинні бути також стійкими простими числами. Число P є стійким (strong), якщо воно відповідає 3 умовам:
-
P- 1 має великий простий дільник, позначимо його як r (тобто P = r + 1 (mod r)); -
P+ 1 має великий простий дільник, позначимо як s (тобто P = s 1 (mod s)); -
r- 1 має великий простий дільник, позначимо його як t (тобто r = 1 (mod t)).
Умова 1 не дозволить успішно факторизувати N методом Полларда, який дозволяє швидко розкласти число N на множники, якщо P - 1 має невеликі (скажімо менше мільйона) прості дільники. Умова 2 дозволить захиститись від методу Ульямса, що дозволяє розкласти N за умови, що P + 1 має невеликі дільники. Умова 3 дозволить захиститись від методу безключового читання RSA (циклічної атаки).
Якщо P вибирається випадково і має досить великий розмір, то, як правило, P – 1 та P+1 матимуть великі прості дільники. Проте вибір стійких простих чисел не захищає систему від атаки алгоритмом факторизації з урахуванням еліптичних кривих.
Отримати стійкі прості числа можна в такий спосіб. Генеруємо великі прості числа s та t. Потім отримуємо таке число r, що r - 1 ділиться на t (для цього розглядаємо непарні числа виду kt + 1 де k - послідовні натуральні числа, і перевіряємо їх на простоту, поки не знайдемо просте). Потім обчислюючи P = ((sr - 1 - rs - 1) mod rs) + xrs, де x - деяке ціле число і перевіряючи P простоту, знаходимо стійке просте число P.
Якщо число K вибирається випадковим чином, одним із способів прискорення обчислень (тобто зменшення числа зведень у ступінь) є наступний алгоритм швидкого зведення, наприклад: