Файл: Введение в горнодобывающей промышленности выработки широко используются для разработки полезных ископаемых.docx
Добавлен: 11.12.2023
Просмотров: 122
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
— компоненты тензора напряжений в нетронутом массиве горных пород; а — радиус сечения выработки; r, — текущие полярные координаты.
Как следует из уравнений (3.1) и (3.2), напряжения в любой точке массива пород вокруг кругового сечения определяются соотношением напряжений в нетронутом массиве и координатами данной точки.
Причем в случае равнокомпонентного поля естественных напряжений (например, для вертикальных стволов при действии в массиве только гравитационных сил) коэффициент концентрации тангенциальных напряжений, т.е. коэффициент, показывающий во сколько раз напряжение в данной точке превышает соответствующее напряжение в нетронутом массиве (К = i / ), в любой точке контура равен максимально К = 2 и все напряжения являются сжимающими (рис. 3.4).
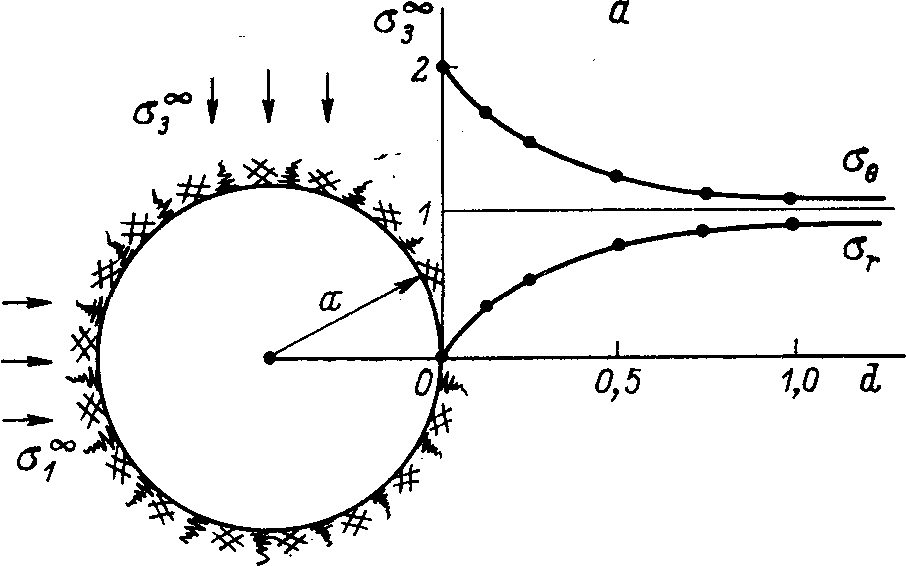
Рис. 3.4. Распределение напряжений вокруг выработки кругового поперечного сечения при равнокомпонентном напряжённом состоянии нетронутого массива (3 = 1).
При неравнокомпонентном поле напряжений (31) на части контура выработки со стороны действия большего из напряжений появляется область растягивающих напряжений, которая тем обширнее, чем больше разница между 3и1. Сжимающие же напряжения в противоположность этому имеют большие значения со стороны действия меньших нагрузок.
Рассмотрим несколько частных случаев.
1. Выработка горизонтальная. Естественное поле в массиве пород - гравитационное, соответствует гипотезе академика АН СССР А.Н. Динника, т.е. отношение горизонтальной компоненты к вертикальной 1/3 = /(1-). При = 0.2 горизонтальное напряжение 1 = 0.253 (рис. 3.5).
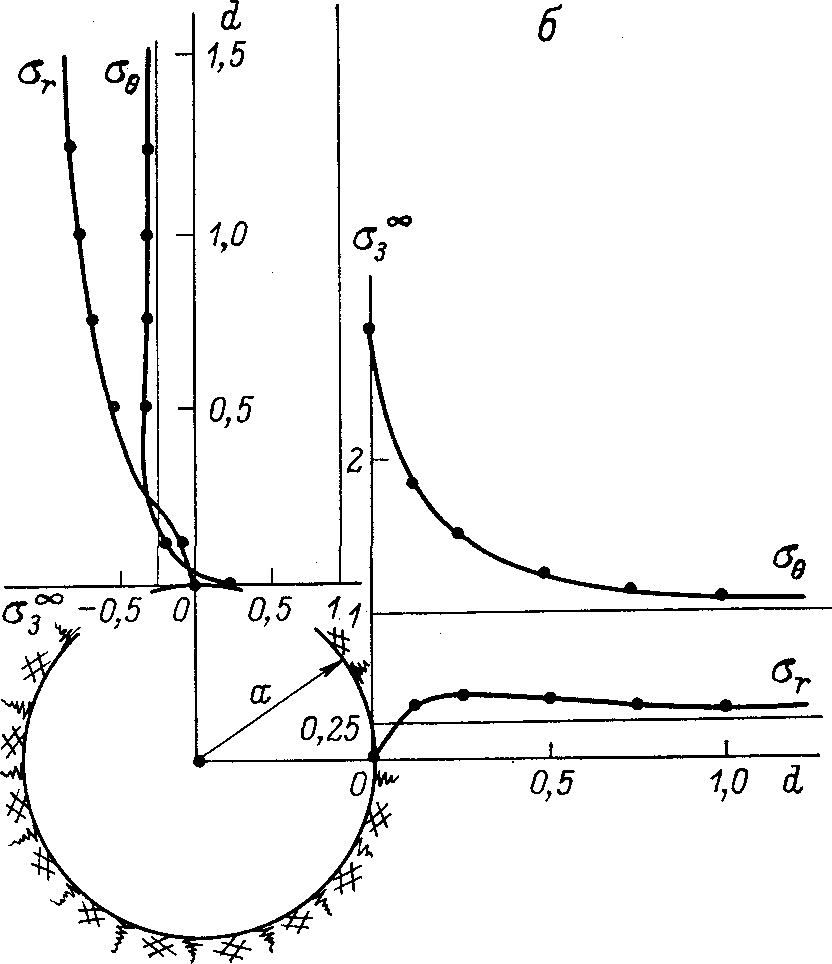
Рис. 3.5. Распределение напряжений в кровле и стенках горизонтальной выработки кругового поперечного сечения при соотношениях компонент тензора напряжений в нетронутом массиве по А.Н. Диннику (при v = 0,2;
1 = 0.25 3)
В этом случае максимальный коэффициент концентрации напряжений К наблюдается в боках выработки и составляет 2,75. В кровле образуется небольшая зона растяжений.
2. Выработка горизонтальная. Естественное поле в массиве пород - гравитационно-тектоническое, т.е. горизонтальное напряжение 1 = 23 (рис. 3.6а) и 1 = 103(рис. 3.6б).
При этом максимальная концентрация напряжений наблюдается в кровле горизонтальной выработки, коэффициенты концентрации составляют соответственно 5 и 29.
Во всех рассмотренных случаях речь идет о коэффициенте концентрации тангенциальных напряжений, поскольку радиальные напряжения на контуре всегда равны нулю, если со стороны контура выработки массив не испытывает противодавления (например, реакции жесткой крепи).
Интересно проследить, как изменяется размер L области влияния выработок, т. е. другими словами, на каких расстояниях от контура выработки напряжения практически не отличаются от соответствующих компонент поля напряжений нетронутого массива.
Вычисления по формулам (3.2) показывают, что для условий равнокомпонентного (гидростатического) напряженного состояния нетронутого массива уже на расстоянии, немногим более трёх радиусов выработки [L = 1.65d (где d = 2a)], значения и тангенциальных и радиальных составляющих отличаются от соответствующих компонент напряжений в нетронутом массиве не более, чем на 5%.
Для других условий нагружения наблюдаются существенные различия в скорости затухания компонент напряжений и r по мере удаления от контура выработки. При этом, как правило, быстрее затухают те компоненты, которые имеют большие коэффициенты концентраций на контуре.
Так, при 1=0.253наиболее быстро затухает тангенциальное напряжение в стенке выработки, уже на расстоянии L = 1.35d от контура оно отличается на 5% от значения такового в нетронутом массиве. Остальные компоненты (в том числе и в кровле) затухают медленнее, и указанный уровень достигают лишь на расстоянии L = 2.75d.
При 1=23и 1
=103тоже быстрее затухают в кровле, исходя из этого, радиальная протяженность области влияния выработки составляет соответственно L = 1.5d. и L = 1.25d. Медленнее затухают радиальные составляющие напряжений. В частности, в стенке значение r в первом случаеотличается на 5% от уровня соответствующей компоненты нетронутого массива на расстоянии L = 2.5d от контура. Особенно медленно уменьшаются радиальные составляющие в кровле во втором случае (L = 7d).
Таким образом, размеры зоны влияния выработок существенно зависят от степени равномерности начального поля напряжений и минимально, при наиболее благоприятном случае, для круговой формы сечения составляют около полутора диаметров.
Представляет практический интерес характер распределения напряжений в массиве в сторону забоя выработки. В данном случае напряженное состояние массива уже нельзя отождествлять с распределением напряжений в плоскости продольного сечения выработки и необходимо рассматривать пространственную задачу. Результаты исследований свидетельствуют, что в самом простом случае, если конфигурацию забоя представить приближённо полусферой, а начальное поле напряжений в массиве является равнокомпонентным (гидростатическим)
1 = 2 = 3, компоненты напряжений определяются формулами в сферической системе координат (; r; )
= = 1[1 + a3 / 2 r3](3.3)
r = 1[1 - a3 / r3].
В этом случае (рис. 3.7) размеры зоны влияния и значения коэффициентов концентрации существенно меньше, чем для плоской постановки. В частности, уже на расстоянии L=0,8 d от контура выработки компоненты напряжении весьма мало отличаются от таковых в нетронутом массиве, а коэффициент концентрации тангенциальных напряжений на контуре К = 1,5.
Р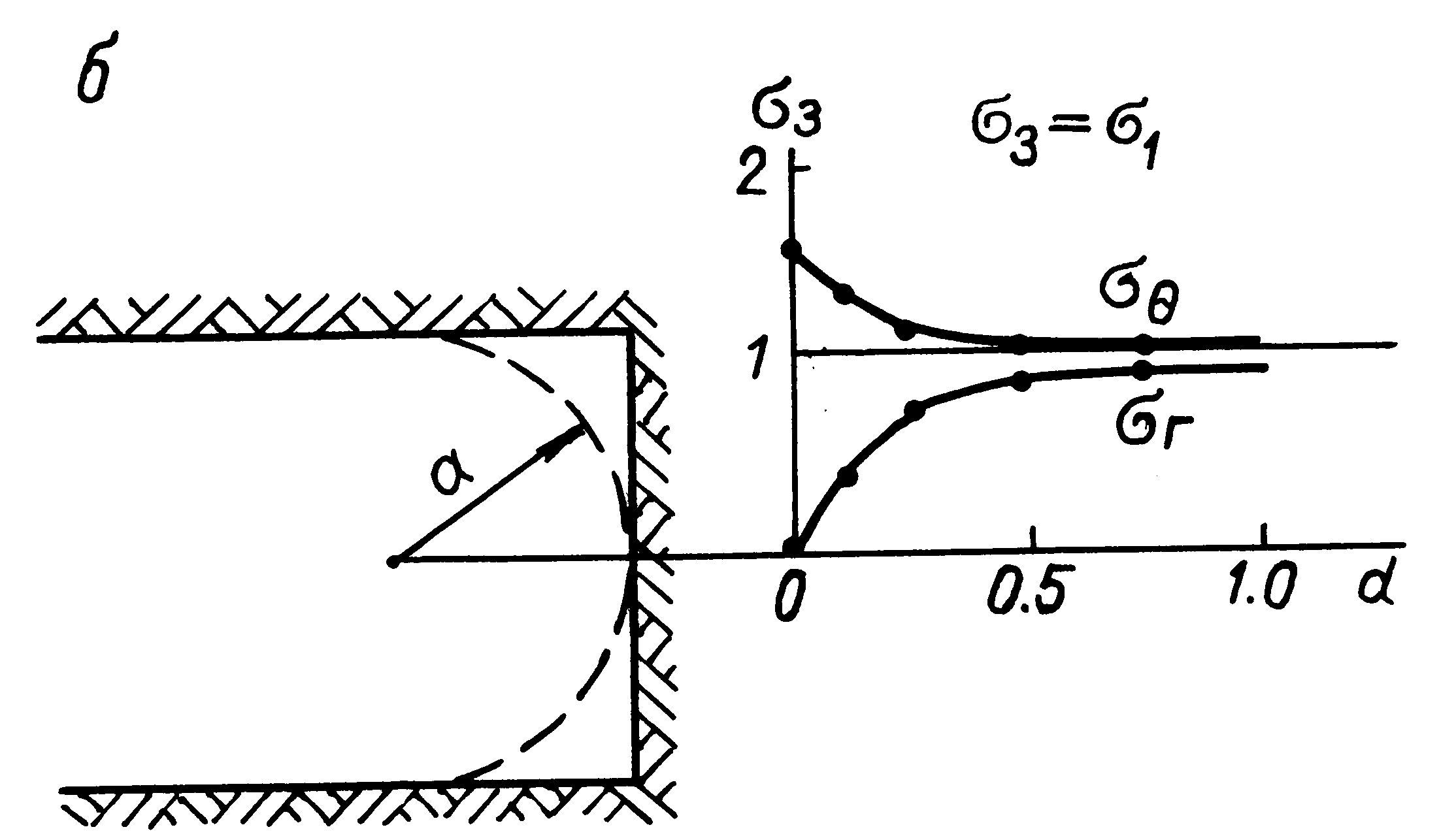
ис. 3.7. Распределение напряжений вокруг забоя выработки кругового поперечного сечения.
Чтобы проследить, как изменяются напряжения в массиве пород в зависимости от формы сечений выработок, рассмотрим случаи, когда выработки имеют эллиптические, прямоугольные и сводчатые поперечные сечения.
В практике горного дела эллиптическую форму поперечного сечения иногда применяют для вертикальных стволов.
На рис. 3.8 представлены графики напряжений вокруг эллиптического отверстия с отношением осей а/б = 2, при тех же соотношениях компонент начального напряженного состояния, как и для круговой формы сечения выработок.
Из сопоставления графиков на рис. 3.5; 3.6; и 3.8 следует, что в целом характер распределения напряжений вокруг эллиптического отверстия подобен таковому при круговом сечении. Однако коэффициенты концентрации тангенциальных напряжений отличаются от соответствующих им коэффициентов при круговой форме.
По сравнению с круговой формой сечения выработок эллиптическое сечение характеризуется несколько большими скоростями затухания напряжений по мере удаления в сторону массива, т. е. меньшей областью влияния. В частности, для наиболее благоприятных случаев, размеры области влияния эллиптического сечения составляют около 1.2 большого диаметра (разница между напряжениями на границе области влияния и в нетронутом массиве не превышает 5%).
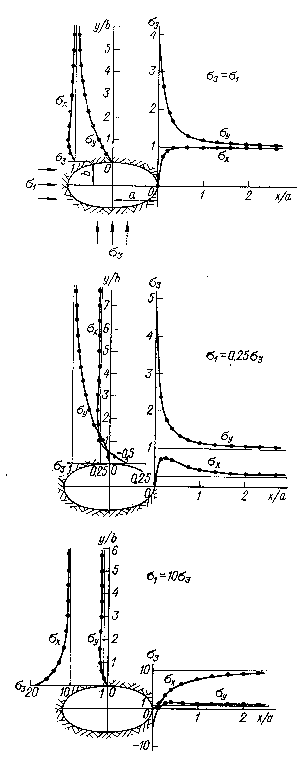
Рис. 3.8. Распределение напряжений в стенках выработки эллиптического поперечного сечения с соотношением осей а/б=2 при различных компонентах тензора напряжений в нетронутом массиве.
На напряжения вокруг выработки эллиптического сечения влияют соотношение полуосей сечения и (что особенно важно) ориентировка осей сечения в поле напряжений 1 и 3нетронутого массива.
Фактически, это один из элементов управления состоянием приконтурного массива вокруг выработок в случае их эллиптического сечения:
Максимальная устойчивость выработки достигается при соблюдении равенства а/б = 3/ 1 и при расположении большей оси сечения по линии действия наибольшего из напряжении в нетронутом массиве.
Это необходимо иметь в виду при проектировании горных выработок, выборе их оптимальных направлений и ориентации поперечного сечения.
Отмеченные закономерности можно проследить и при рассмотрении графиков напряжений вокруг сечений выработок прямоугольной и сводчатой формы (рис. 3.9). Однако в этих случаях напряжения уже не могут быть представлены в виде элементарных уравнений, и их вычисляют с помощью более сложных математических методов.
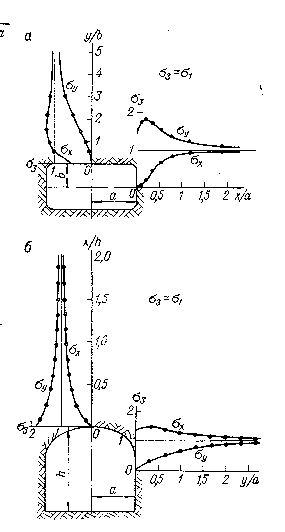
Рис. 3.9. Распределение напряжений в стенках выработки прямоугольной (а) и сводчатой (б) форм поперечного сечения.
Если в качестве модели массива применяется упругая анизотропная модель, в частности, модель трансверсально-изотропного тела, то характер распределения напряжений вокруг выработок изменяется.
В настоящее время разработана теория упругости анизотропной среды, позволяющая вычислять напряжения вокруг отверстий различной конфигурации, однако лишь отдельные решения доведены непосредственно до числа. При этом имеющиеся данные об анизотропии упругих свойств пород свидетельствуют о незначительных отличиях значений напряжений вокруг выработок в анизотропных массивах от изотропного случая.
Теоретические работы о распределении напряжений в физически нелинейных упругих средах показывают, что при этом коэффициенты концентрации напряжений вокруг отверстий различной формы, в отличие от случая линейного деформирования, существенно зависят от упругих характеристик среды и значений внешних нагрузок.
Как следует из уравнений (3.1) и (3.2), напряжения в любой точке массива пород вокруг кругового сечения определяются соотношением напряжений в нетронутом массиве и координатами данной точки.
Причем в случае равнокомпонентного поля естественных напряжений (например, для вертикальных стволов при действии в массиве только гравитационных сил) коэффициент концентрации тангенциальных напряжений, т.е. коэффициент, показывающий во сколько раз напряжение в данной точке превышает соответствующее напряжение в нетронутом массиве (К = i / ), в любой точке контура равен максимально К = 2 и все напряжения являются сжимающими (рис. 3.4).
Рис. 3.4. Распределение напряжений вокруг выработки кругового поперечного сечения при равнокомпонентном напряжённом состоянии нетронутого массива (3 = 1).
При неравнокомпонентном поле напряжений (31) на части контура выработки со стороны действия большего из напряжений появляется область растягивающих напряжений, которая тем обширнее, чем больше разница между 3и1. Сжимающие же напряжения в противоположность этому имеют большие значения со стороны действия меньших нагрузок.
Рассмотрим несколько частных случаев.
1. Выработка горизонтальная. Естественное поле в массиве пород - гравитационное, соответствует гипотезе академика АН СССР А.Н. Динника, т.е. отношение горизонтальной компоненты к вертикальной 1/3 = /(1-). При = 0.2 горизонтальное напряжение 1 = 0.253 (рис. 3.5).
Рис. 3.5. Распределение напряжений в кровле и стенках горизонтальной выработки кругового поперечного сечения при соотношениях компонент тензора напряжений в нетронутом массиве по А.Н. Диннику (при v = 0,2;
1 = 0.25 3)
В этом случае максимальный коэффициент концентрации напряжений К наблюдается в боках выработки и составляет 2,75. В кровле образуется небольшая зона растяжений.
2. Выработка горизонтальная. Естественное поле в массиве пород - гравитационно-тектоническое, т.е. горизонтальное напряжение 1 = 23 (рис. 3.6а) и 1 = 103(рис. 3.6б).
При этом максимальная концентрация напряжений наблюдается в кровле горизонтальной выработки, коэффициенты концентрации составляют соответственно 5 и 29.
Во всех рассмотренных случаях речь идет о коэффициенте концентрации тангенциальных напряжений, поскольку радиальные напряжения на контуре всегда равны нулю, если со стороны контура выработки массив не испытывает противодавления (например, реакции жесткой крепи).
Интересно проследить, как изменяется размер L области влияния выработок, т. е. другими словами, на каких расстояниях от контура выработки напряжения практически не отличаются от соответствующих компонент поля напряжений нетронутого массива.
Вычисления по формулам (3.2) показывают, что для условий равнокомпонентного (гидростатического) напряженного состояния нетронутого массива уже на расстоянии, немногим более трёх радиусов выработки [L = 1.65d (где d = 2a)], значения и тангенциальных и радиальных составляющих отличаются от соответствующих компонент напряжений в нетронутом массиве не более, чем на 5%.
Для других условий нагружения наблюдаются существенные различия в скорости затухания компонент напряжений и r по мере удаления от контура выработки. При этом, как правило, быстрее затухают те компоненты, которые имеют большие коэффициенты концентраций на контуре.
Так, при 1=0.253наиболее быстро затухает тангенциальное напряжение в стенке выработки, уже на расстоянии L = 1.35d от контура оно отличается на 5% от значения такового в нетронутом массиве. Остальные компоненты (в том числе и в кровле) затухают медленнее, и указанный уровень достигают лишь на расстоянии L = 2.75d.
При 1=23и 1
=103тоже быстрее затухают в кровле, исходя из этого, радиальная протяженность области влияния выработки составляет соответственно L = 1.5d. и L = 1.25d. Медленнее затухают радиальные составляющие напряжений. В частности, в стенке значение r в первом случаеотличается на 5% от уровня соответствующей компоненты нетронутого массива на расстоянии L = 2.5d от контура. Особенно медленно уменьшаются радиальные составляющие в кровле во втором случае (L = 7d).
Таким образом, размеры зоны влияния выработок существенно зависят от степени равномерности начального поля напряжений и минимально, при наиболее благоприятном случае, для круговой формы сечения составляют около полутора диаметров.
Представляет практический интерес характер распределения напряжений в массиве в сторону забоя выработки. В данном случае напряженное состояние массива уже нельзя отождествлять с распределением напряжений в плоскости продольного сечения выработки и необходимо рассматривать пространственную задачу. Результаты исследований свидетельствуют, что в самом простом случае, если конфигурацию забоя представить приближённо полусферой, а начальное поле напряжений в массиве является равнокомпонентным (гидростатическим)
1 = 2 = 3, компоненты напряжений определяются формулами в сферической системе координат (; r; )
= = 1[1 + a3 / 2 r3](3.3)
r = 1[1 - a3 / r3].
В этом случае (рис. 3.7) размеры зоны влияния и значения коэффициентов концентрации существенно меньше, чем для плоской постановки. В частности, уже на расстоянии L=0,8 d от контура выработки компоненты напряжении весьма мало отличаются от таковых в нетронутом массиве, а коэффициент концентрации тангенциальных напряжений на контуре К = 1,5.
Р
ис. 3.7. Распределение напряжений вокруг забоя выработки кругового поперечного сечения.Чтобы проследить, как изменяются напряжения в массиве пород в зависимости от формы сечений выработок, рассмотрим случаи, когда выработки имеют эллиптические, прямоугольные и сводчатые поперечные сечения.
В практике горного дела эллиптическую форму поперечного сечения иногда применяют для вертикальных стволов.
На рис. 3.8 представлены графики напряжений вокруг эллиптического отверстия с отношением осей а/б = 2, при тех же соотношениях компонент начального напряженного состояния, как и для круговой формы сечения выработок.
Из сопоставления графиков на рис. 3.5; 3.6; и 3.8 следует, что в целом характер распределения напряжений вокруг эллиптического отверстия подобен таковому при круговом сечении. Однако коэффициенты концентрации тангенциальных напряжений отличаются от соответствующих им коэффициентов при круговой форме.
По сравнению с круговой формой сечения выработок эллиптическое сечение характеризуется несколько большими скоростями затухания напряжений по мере удаления в сторону массива, т. е. меньшей областью влияния. В частности, для наиболее благоприятных случаев, размеры области влияния эллиптического сечения составляют около 1.2 большого диаметра (разница между напряжениями на границе области влияния и в нетронутом массиве не превышает 5%).
Рис. 3.8. Распределение напряжений в стенках выработки эллиптического поперечного сечения с соотношением осей а/б=2 при различных компонентах тензора напряжений в нетронутом массиве.
На напряжения вокруг выработки эллиптического сечения влияют соотношение полуосей сечения и (что особенно важно) ориентировка осей сечения в поле напряжений 1 и 3нетронутого массива.
Фактически, это один из элементов управления состоянием приконтурного массива вокруг выработок в случае их эллиптического сечения:
Максимальная устойчивость выработки достигается при соблюдении равенства а/б = 3/ 1 и при расположении большей оси сечения по линии действия наибольшего из напряжении в нетронутом массиве.
Это необходимо иметь в виду при проектировании горных выработок, выборе их оптимальных направлений и ориентации поперечного сечения.
Отмеченные закономерности можно проследить и при рассмотрении графиков напряжений вокруг сечений выработок прямоугольной и сводчатой формы (рис. 3.9). Однако в этих случаях напряжения уже не могут быть представлены в виде элементарных уравнений, и их вычисляют с помощью более сложных математических методов.
Рис. 3.9. Распределение напряжений в стенках выработки прямоугольной (а) и сводчатой (б) форм поперечного сечения.
Если в качестве модели массива применяется упругая анизотропная модель, в частности, модель трансверсально-изотропного тела, то характер распределения напряжений вокруг выработок изменяется.
В настоящее время разработана теория упругости анизотропной среды, позволяющая вычислять напряжения вокруг отверстий различной конфигурации, однако лишь отдельные решения доведены непосредственно до числа. При этом имеющиеся данные об анизотропии упругих свойств пород свидетельствуют о незначительных отличиях значений напряжений вокруг выработок в анизотропных массивах от изотропного случая.
Теоретические работы о распределении напряжений в физически нелинейных упругих средах показывают, что при этом коэффициенты концентрации напряжений вокруг отверстий различной формы, в отличие от случая линейного деформирования, существенно зависят от упругих характеристик среды и значений внешних нагрузок.