Файл: за мерзімді жоспар блімі 3а бір айнымалысы бар сызыты тедеу Мектеп Тараз аласы фмб нзм.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Қысқа мерзімді жоспар
| Ұзақ мерзімді жоспар бөлімі: 6.3А Бір айнымалысы бар сызықтық теңдеу | Мектеп: Тараз қаласы ФМБ НЗМ | ||||||||||||||||||
| Күні: | Мұғалімнің аты-жөні: | ||||||||||||||||||
| Сынып: 6 | Қатысқандар саны: | Қатыспағандар саны: | |||||||||||||||||
| Сабақ тақырыбы | Теңдеулер көмегімен мәтінді есептерді шығару | ||||||||||||||||||
| Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме) | 6.5.1.6 мәтінді есептерді сызықтық теңдеулерді құру арқылы шығару; | ||||||||||||||||||
| Сабақ мақсаттары | Бір айнымалысы бар сызықтық теңдеулер туралы біледі және оның қасиеттерін есептер шешуде қолданады | ||||||||||||||||||
| Бағалау критерийлері | Оқушы: - сызықтық теңдеудің және оның түбірлерінің анықтамасын білу, мәндес теңдеулер ұғымын түсіну. - сызықтық теңдеулерді шешу үшін қасиеттерін қолдану. - қай жағдайда теңдеудің түбірі болмайды, жалғыз болады және шексіз көп болатын шарттарын ажырату; мәтінмен берілген есептердің шартына байланысты теңдеуін құрады және оны шешеді. | ||||||||||||||||||
| Тілдік мақсаттар | Оқушылар: мәтін есептің берілгеніне сәйкес математикалық моделін құрастыру алгоритмін сипаттайды. Пәнге тән лексика мен терминология:
Диалог пен жазу үшін пайдалы сөздер мен тіркестер:
| ||||||||||||||||||
| Құндылықтарды дарыту | Жаңа білімді меңгеру арқылы өмір бойы оқу құндылығын қалыптастыру. | ||||||||||||||||||
| Пәнаралық байланыстар | Физика | ||||||||||||||||||
| АКТ қолдану дағдылары | | ||||||||||||||||||
| Бастапқы білім | Алгебралық өрнектерді ықшамдау, жақшаларды ашу, ұқсас қосылғыштарды біріктіру. | ||||||||||||||||||
| Сабақ барысы | |||||||||||||||||||
| Сабақтың жоспарланған кезеңдері | Сабақтағы жоспарланған іс-әрекет | Ресурстар | |||||||||||||||||
| Сабақтың басы | І. Ұйымдастыру кезеңі. Сәлемдесу. Оқушыларды түгелдеу. Оқушылардың сабаққа дайындығын тексеру Сыныпты 3 топқа біріктіру | | |||||||||||||||||
| Сабақ мақсатын анықтау | ІІ. Сабақтың тақырыбы мен мақсатын анықтау үшін белсенді әдіс тәсілдерді қолдану. 1-топ. 2,3х=9,2 2-топ. 7х+3=7х+5 3-топ. 2х+х-5=3х-5 Түріндегі теңдеулерді әр топта шешеді. Жауаптарын плакатқа жазады. Белгіленген уақытта сағат тілімен бір-бірінің плакаттарын алмасады. Әр тапсырманы топтарында талқылап, қажет болған жағдайда өз жауап үлгісін ұсынады. Соңында әр топ тапсырмасын барлық топ мүшелері талқылайды, - қандай жаңа білім алдыңыз? - сіз үшін не қызық болды? - сіз нені өзгертер едіңіз? – деген сұрақтар бойынша өз ойларын білдіре отырып, сабақ тақырыбы мен мақсаты анықталады. Сабақ тақырыбы мен мақсатын тұжырымдау және жазу. Негізгі білімді белсендіру. | «Карусель» әдісі Слайд 1-5 | |||||||||||||||||
| Жаңа білімді меңгеру | ІІІ. Жаңа білім мазмұны. Мысал қарастыру: «Бірінші сөредегі кітаптар саны екінші сөредегі кітаптар санынынан 4 есе көп, егер бірінші сөреден 15 кітапты алып, екінші сөреге ауыстырса, онда сөредегі кітаптар тең болады. Екінші сөреде қанша кітап бар? Шешу жолы: Екінші сөредегі кітаптарды х деп белгілейік. Онда бірінші сөредегі кітаптар саны 4х болады. Егер бірінші сөредегі 15 кітапты екінші сөреге ауыстырғанда, бірінші сөреде 4х-15 кітап, ал екінші сөреде х+15 кітап болады. Есеп шарты бойынша мұндай ауыстырудан кейін екі сөреде кітаптар саны тең болады. Олай болса, 4х-15=х+15 Біз белгісіз кітаптар санын табу үшін құрамында айнымалысы бар теңдік құрдық. Мұндай теңдіктерді бір айнымалысы бар теңдеулер немесе бір белгісізі бар теңдеулер деп атайды. Бізге 4х-15=х+15 теңдеуіндегі х айнымалысының орнына қойғанда тура теңдік шығатын санды табу керек. Мұндай санды теңдеудің шешімі немесе теңдеудің түбірі деп атайды. Анықтама. Теңдеуді тура теңдікке айналдыратын айнымалының мәні теңдеудің түбірі деп аталады. Теңдеуді шешу дегеніміз – оның түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеу. Анықтама: Түбірлері бірдей болатын теңдеулерді мәндес теңдеулер деп атайды. Мысал: 5х=25, 3х=15 және 4х-2х=10 теңдеулері – мәндес теңдеулер. Түбірлері бірдей: х=5 Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады. Теңдеулерді шешу үшін келесі қасиеттер қолданылады Теңдеулердің 1- қасиеті. Теңдеудің екі жағына да бірдей санды немесе әріпті өрнекті қосқанда (азайтқанда) теңдеу мәндес теңдеуге түрленеді. Мысал. х+24=40, х+24-24=40-24, х=40-24 х=16 – теңдеудің түбірі. Теңдеулердің 2- қасиеті. Теңдеудің екі жағын да нөлден өзге бірдей санға көбеткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді. Мысал. 7х=56 7х:7=56:7, х=8 Қысқаша: 7х=56 х=56:7, х=8 Теңдеулердің бұл қасиеттері тура санды теңдіктердің қасиеттерімен дәлелденеді. Тура санды теңдіктердің қасиеттерін есімізге түсірейік. Тура сандық теңдіктің қасиеттері
Ең алғаш қарастырған мысалымызға оралайық. Есеп шарты бойынша құрылған теңдеуімізді шешейік. 4х-15=х+15 1 – қасиет бойынша: 4х-х=15+15 3х=30 2 – қасиет бойынша: х=30:3 x=10 10 саны – теңдеудің түбірі. Енді біз сұраққа жауап бере аламыз. Екінші сөреде 10 кітап болды. Көптеген теңдеулерді теңдеулердің қасиеттерін қолдана отырып aх=b түріне келтіруге болады. aх=b түріндегі теңдеуді бір айнымалысы бар сызықтық теңдеу деп атайды. Мұндағы aжәне b – қандай да бір сандар. х – айнымалы. Мысал. 5х=-3, -0,2х=0 aх=b теңдеуін шешіп, түбірін табуда келесі үш жағдай орындалады:
Бір айнымалысы бар сызықтық теңдеуді шешу үшін алгоритмі: Қарастырылған мысалдарға талдау жасасақ, сызықтық теңдеулерді шешу кезінде келесі алгоритм орындалатынын байқауға болады. Алгоритм: 1. Теңдеудің оң жақ немесе сол жақ бөлігіндегі өрнектерде жақшалар болса, онда оларды ереже бойынша ашу керек. 2. Айнымалысы бар мүшелерді теңдеудің сол жағына, бос мүшелерді теңдеудің оң жағына жинақтау керек. 3. Теңдеудегі ұқсас мүшелерді біріктіріп, теңдеуді ax = b түріне келтіру керек. 4. Берілген теңдеуге мәндес соңғы теңдеуді a және b коэффициенттерінің мәніне байланысты шешу керек. | Слайд | |||||||||||||||||
| Білімді қолдануға тапсырмалар орындау | Тапсырма. Теңдеулердің қасиеттерін қолданып, келесі теңдеулерді сызықтық түрге келтіріңіз: а) 3х – 11 = 5х + 7; Шешуі: а) 3х – 11 = 5х + 7; 3х – 5х =7 + 11; –2х = 18. б) 2 (х + 1) = 2х + 2; 2х + 2 = 2х + 2; 2х – 2х = 2 – 2; 0 · х = 0. в) –8х + 11 = 8 (3 – х). –8х + 11 = 24 – 8х; –8х + 8х = 24 – 11; 0 · х = 13. a және b коэффициенттері неге тең және теңдеудің қанша түбірі бар? а)a = –2; b = 18 – бір түбір х = –9, екі жағын да (–2) ге бөлдік. б) a = 0; b = 0 – сансыз көп түбір, себебі 0 · х = 0 теңдігі х – тің кез келген мәнінде тура. в) a = 0; b = 13 – түбірі жоқ, себебі 0 · х = 13 х – тің ешбір мәнінде орындалмайды. Оқулықпен жұмыс. №842, №843 (есепті теңдеу құру арқылы шығару) | Слайд Математика 6 сынып Алдамұратова | |||||||||||||||||
| Сабақтың соңы | Мақсат: оқушылардың рефлексиясы, кері байланыс. Оқушылар рефлексиясы үшін сұрақтар:
Оқушылар өз жұмысын және сыныптастарының жұмысын бағалау критерийлері арқылы бағалайды. | | |||||||||||||||||
| Саралау –оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз? | Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз? | Денсаулық және қауіпсіздік техникасының сақталуы | |||||||||||||||||
| Жұптық жұмысты бақылай отырып, қиындықтар кездескенденде бағыт беремін. Өздеріне сенімсіз оқушыларды өздеріне сенімді оқушылармен біріктіремін. | Оқушылардың тапсырманы орындаудағы белсенділіктрін бақылау арқылы формативті бағалаймын. Сабақ соңында оқушылар өздерінің жеткен жетістіктері жайлы ауызша өзін – өзі бағалайды. | Белсенді әдіс-тәсілдерді қолдану арқылы жүзеге асырамын, қажет болған жағдайда сергіту сәтін орындатамын. | |||||||||||||||||
| Сабақ бойынша рефлексия Сабақ мақсаттары/оқу мақсаттары дұрыс қойылған ба? Оқушылардың барлығы ОМ қол жеткізді ме? Жеткізбесе, неліктен? Сабақта саралау дұрыс жүргізілді ме? Сабақтың уақыттық кезеңдері сақталды ма? Сабақ жоспарынан қандай ауытқулар болды, неліктен? | Бұл бөлімді сабақ туралы өз пікіріңізді білдіру үшін пайдаланыңыз. Өз сабағыңыз туралы сол жақ бағанда берілген сұрақтарға жауап беріңіз. | ||||||||||||||||||
| | |||||||||||||||||||
| Жалпы баға Сабақтың жақсы өткен екі аспектісі (оқыту туралы да, оқу туралы да ойланыңыз)? 1: 2: Сабақты жақсартуға не ықпал ете алады (оқыту туралы да, оқу туралы да ойланыңыз)? 1: 2: Сабақ барысында сынып туралы немесе жекелеген оқушылардың жетістік/қиындықтары туралы нені білдім, келесі сабақтарда неге көңіл бөлу қажет? | |||||||||||||||||||
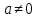 болса, теңдеудің екі жағын да а –ға бөліп,
болса, теңдеудің екі жағын да а –ға бөліп, 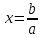 теңдігін жазамыз. Бұл жағдайда теңдеудің бір ғана түбірі бар.
теңдігін жазамыз. Бұл жағдайда теңдеудің бір ғана түбірі бар.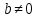 болса, теңдеу
болса, теңдеу 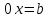 түрінде жазылады.
түрінде жазылады.