Древние индийцы изобрели для каждой цифры свой знак. Вот как они выглядели (Рис.6)


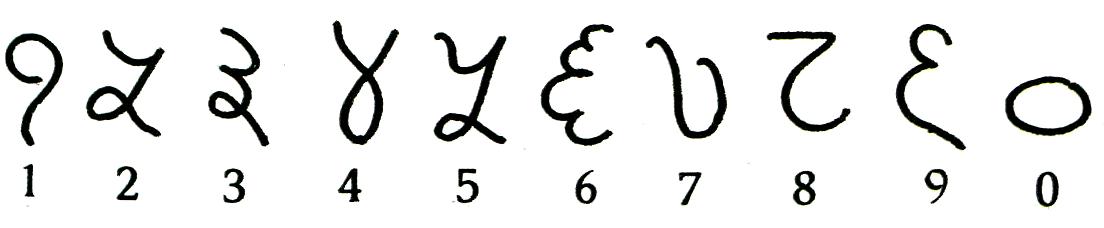
Рис. 6.
Однако Индия была оторвана от других стран, - на пути лежали тысячи километров расстояния и высокие горы. Арабы были первыми «чужими», которые заимствовали цифры у индийцев и привезли их в Европу. Чуть позже арабы упростили эти значки, они стали выглядеть вот так (Рис.7).


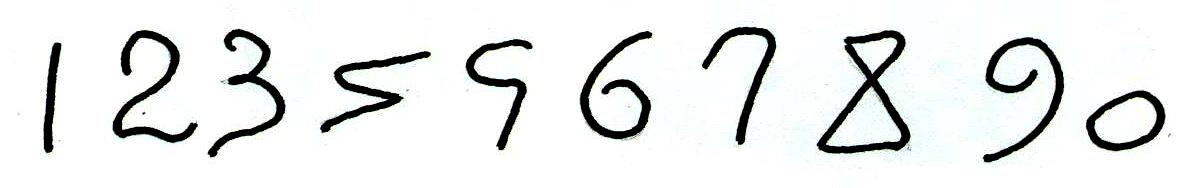
Рис. 7.
Они похожи на многие наши цифры. Слово «цифра» тоже досталось нам от арабов по наследству. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Арабские цифры были видоизменёнными изображениями индийских цифр приспособленными к арабскому письму. (рис.8)
Впервые индийскую систему записи использовал арабский учёный Мухаммед ибн Муса аль-Хорезми, автор знаменитой Китаб аль-Джебр ва-ль-Мукабаля, от названия которой произошёл термин «алгебра».


Рис. 8

Китайские цифры, так же как и другие символы письменности, обозначаются иероглифами. (рис.9) Такое обозначение непривычно для европейцев, поскольку цифры представлены в виде непривычных нам символов. Составные числа образуются комбинацией символов в определенном порядке.


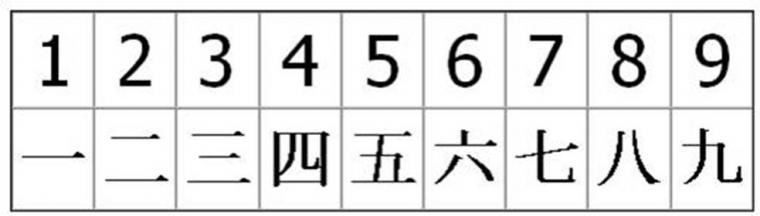
Рис. 9


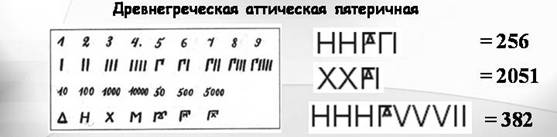
В Древней Греции и в последствие в Византии были две основные системы греческие чисел - более древняя аттическая система и пришедшая ей на смену ионическая. Переводчик чисел Титло работает с обеими системами греческих чисел. 

Собственно, первые записи греческих чисел появились видимо на Крите, в XIV-VII веках до н. э. К сожалению, сведений о них у меня недостаточно, чтобы включить критскую систему в переводчик. 




Постепенное превращение первоначальных цифр в наши современные цифры.

2. 
   Римская нумерация
   

---

В основе римской нумерации использованы принципы сложения (например, VI = V + I) и вычитания (например, IX = X -1). Римская система нумерации десятичная, но непозиционная. Римские цифры произошли не от букв. Первоначально они обозначались, как и у многих народов, «палочками» (I - один, X - 10 - перечеркнутая палочка, V - 5 - половина от десяти, сто - кружочек с черточкой внутри, пять­десят — половина этого знака и т. д.).

Со временем некоторые знаки изменились: С - сто, L - пятьде­сят, М - тысяча, D - пятьсот. Например: XL - 40, LXXX - 80, ХС - 90, CDLIX - 459, CCCLXXXII - 382, CMXCI - 991, MCMXCVIII - 1998, MMI – 2001.
3.3. Цифры русского народа

Арабские числа в России стали применять, в основном, с XVIII века. До того наши предки использовали славянскую нумерацию. Над бук­вами ставились титлы (черточки), и тогда буквы обозначали числа.

В одной из русских рукописей XVIII века написано: «... Знай же то, что есть сто и что есть тысяща, и что есть тма, и что есть легион, и что есть леодр...; ... сто есть десятью десять, а тысяща есть десять сот, а тма десять тысящ, а легион есть десять тем, а леодр есть де­сять легионов...».

П 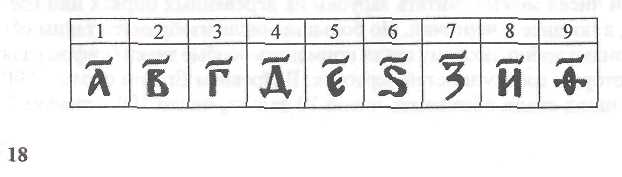ервые девять чисел записывались так:

Сотни миллионов назывались «колодами».

« Колода» имела специальное обозначение: над буквой и под бук­вой ставили квадратные скобки. Например, число 108 записывалось в виде

Числа от 11 до 19 обозначались так:



Остальные числа записывались буквами слева направо, напри­мер, числа 5044 или 1135 имели соответственно обозначение



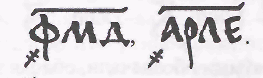
В приведенной системе обозначения чисел не шли дальше ты­сяч миллионов. Такой счет назывался «малый счет». В некоторых рукописях авторами рассматривался и «великий счет», доходив­ший до числа 10⁵⁰. Далее говорилось: «И более сего несть челове­ческому уму разумети».

Заключение

По окончанию работы можно сделать следующие выводы:

1. 
   Слово математика возникло в Древней Греции в V веке до нашей эры.
   
2. 
   Считать люди научились в незапамятные времена.
   
3. 
   Сначала для счета использовали пальцы рук и ног.
   
4. 
   На более высокой стадии развития люди при счете стали применять разные предметы: камешки, зерна, веревку с бирками.
   
5. 
   Необходимость обозначения чисел привело к образованию специальных знаков-цифр.
   
6. 
   Существуют различные теории о происхождении чисел.
   

---

Изучив историю возникновения цифр, я узнала, что арабские цифры были заимствованы арабами в Индии. Они передали данный способ записи в Европу. Современные цифры отличаются от индийских, т.к. арабы их видоизменили, приспосабливая к своему письму. Способы записи чисел в древнеегипетской нумерации, древнегреческой, славянской кириллической и римской нумерации похожи, различны только сами знаки. Способы записи чисел у древних майя и арабов также схожи. А вот в древнем Китае использовался свой особый способ записи, который называется мультипликативным (т.е. умножение). Таким образом, моя гипотеза, что способы записи чисел у разных народов схожи частично подтвердилась. В ходе исследования я установил, что арабская запись чисел 0, 1, 2, 3,4, 5, 6, 7, 8, 9 наиболее удобна и проста, в отличие, например, от древнекитайской или римской. Я научился изображать цифры теми способами, которыми пользовались наши предки. На сегодняшний день параллельно с арабскими цифрами используются и римские (для обозначения размеров одежды, веков и т.д.)

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 
   Большая математическая энциклопедия / Якушева Г.М. и др. – М.: Филол. О-во «СЛОВО»: ОЛМА-ПРЕСС, 2005. – 639 с.: ил.
   
2. 
   Возникновение и развитие математической науки: Кн. Для учителя. – М.: Просвещение, 1987. – 159 с.: ил.
   
3. 
   Шейнина О. С., Соловьева Г. М. Математика/О. С. Шейнина, Г. М. Соловьева – М.: Изд-во НЦ ЭНАС, 2007. – 208с.
   
4. 
   Энциклопедия для детей. Т.11.Математика / Глав. ред, М.Д.Аксёнова. – М.: Аванта+,1998. – 688 с.: ил.
   
5. 
   Энциклопедия. Мудрость тысячелетий. – М.: ОЛМА-ПРЕСС, 2004. –
   

Автор-составитель В. Балязин. – 848 с.

• 
  Иллюстрированный энциклопедический словарь. Москва. Научное издательство «Большая Российская энциклопедия», 1998год.
  
• 
  «Занимательная арифметика» Перельман Я.И.Москва, Триада-Литера,1994 год.
  
• 
  «Математическая шкатулка» Ф.Ф. Нагибин. Е.С. Канин. Москва, «Просвещение», 1984 год.
  
• 
  «Что такое? Кто такой». Москва. Педагогика, 1990 год.
  
• 
  «Что? Зачем? Почему?». Большая книга вопросов и ответов. Перевод с испанского «Школьникам о математике и математиках». Составитель Лиман М.М Москва, Просвещение. 1989 год.
  
• 
  « «Я познаю мир». Детская энциклопедия. Москва, «Астрель», 2004 год. К. Мишиной, А. Зыковой, Москва, Эксмо, 2006 год.
  
• 
  www.wikipedia.ru http://comp-science.narod.ru/
  
• 
  Demenev/files/history.htm
  

---

---

Смотрите также файлы

• Таырыбы Ммкіндігі шектеулі адамдарды леуметтік рлдерін абылдау проблемасы.docx

• Протокол 1 от 26августа 2022г Согласовано Заместитель директора по увр мухина Е. Р. Утверждаю.doc

• Планконспект проведения занятий с.doc

• 1 понятие и виды избирательных систем.pdf

• Б проектирование, строительство, реконструкция, капитальный ремонт и техническое перевооружение опасных производственных объектов, изготовление, монтаж (демонтаж),.docx