Контрольная работа № 1

Вариант 7

117. Снаряд, летевший со скоростью = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью и₁= 150 м/с. Определить скорость u₂ большего осколка.

Дано:

V=400 м/с; m2 = 0,4 M; V1=150 м/с.

Найти:

V2=?

Решение:

Используем закон сохранения импульса:

.

А так как меньший осколок массой m2 = 0,4 M полетел в противоположном направлении, то .

Нам известно, что масса второго осколка равна m1=M-m2=0,6 M. Подставляем и получаем:

Откуда находим скорость



Так как величина положительная, то её вектор скорости совпадает с выбранными нами направлениями оси x.

127. Из ствола автоматического пистолета вылетела пуля массой m₁ = 10 г со скоростью v = 300 м/с. Затвор пистолета массой m₂ = 200 г прижимается к стволу пружиной, жесткость которой k = 25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

Дано:

m1=10г.; m2= 200г.; k = 25 кН/м; v = 300 м/с.

Найти:

=?

Решение:

Используем закон сохранения импульса:



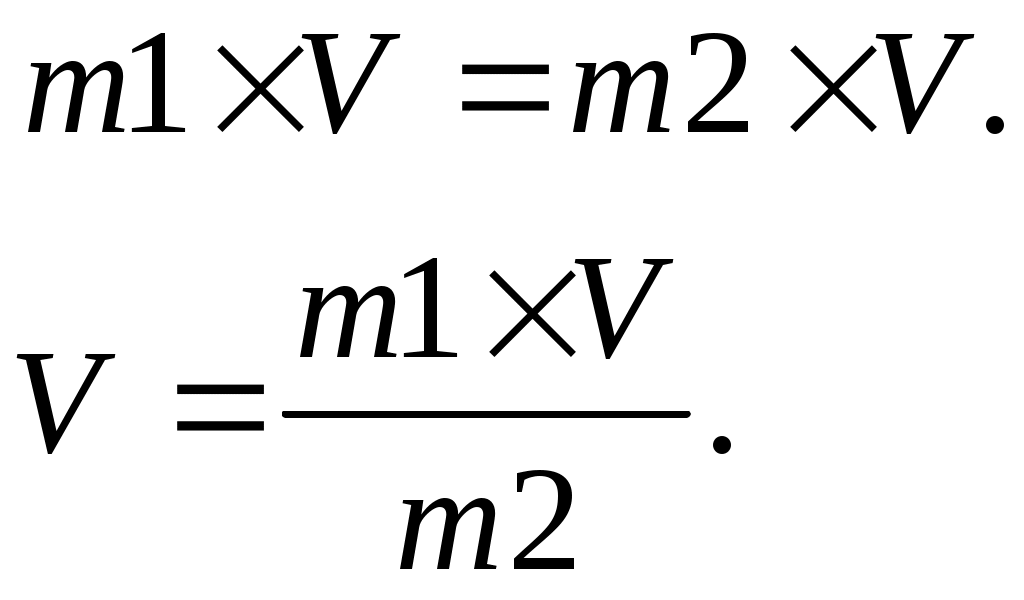
Кинетическая энергия затвора после выстрела:



Подставляем эту скорость

---

в кинетическую энергию затвора:



Эта энергия идет на деформацию пружины. Энергия деформированной пружины:

Тогда

Откуда искомая величина =

187. Во сколько раз релятивистская масса m электрона, обладающего кинетической энергией Т = 1,53 МэВ, больше массы покоя m₀?

Дано:

Т = 1,53 МэВ.

Найти:

=?
Решение:

Так как электрон двигается со скоростью близкой к скорости света необходимо пользоваться релятивистскими формулами для нахождения импульса и энергии частицы.

Масса электрона в состоянии покоя , тогда масса двигающегося электрона

Тогда отношение масс:

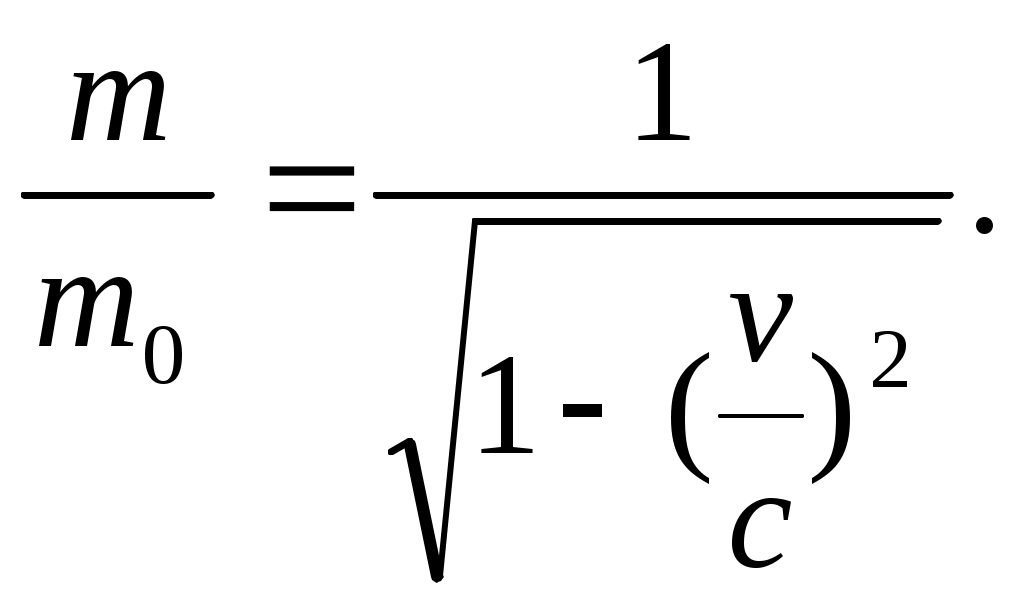
Кинетическая энергия для релятивистской частицы равна:



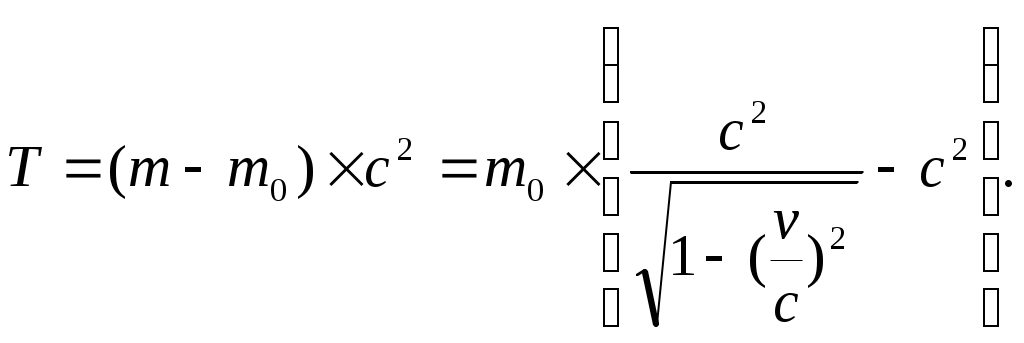
Откуда = ,

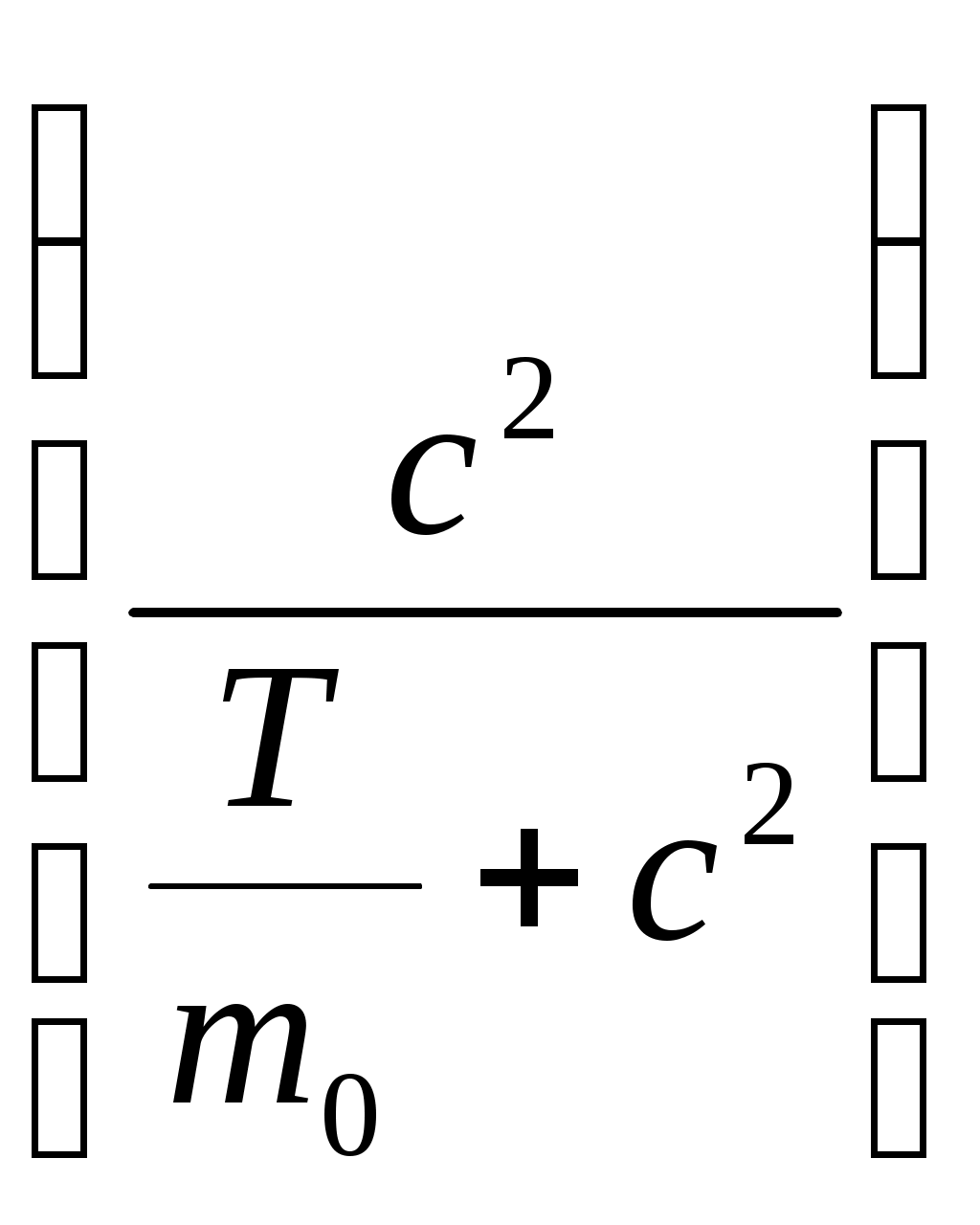поэтому

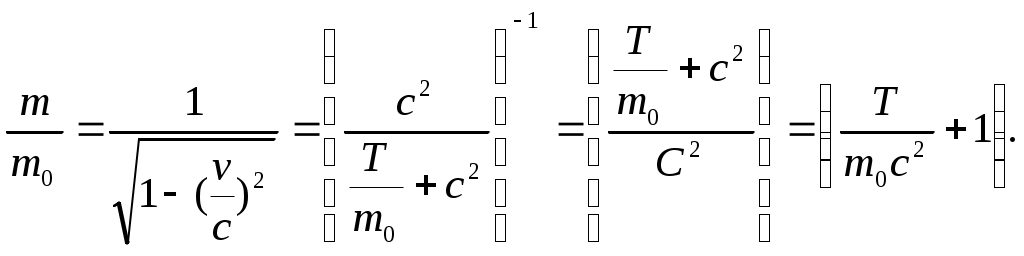
Подставляем числа =

307. В вершинах правильного треугольника со стороной а=10см находятся заряды Q₁ =10 мкКл, Q₂ = 20 мкКл и Q₃=30 мкКл. Определить силу F, действующую на заряд Q₁ со стороны двух других зарядов.

Дано:

а=10см ; Q₁ =10 мкКл; Q₂ = 20 мкКл; Q₃=30 мкКл.
Найти:

F =?

Р ешение:

Cила с которой действует заряд q2 на заряд q1 определяется из закона Кулона

---

где - диэлектрическая постоянная. В нашем случае она равна =1.

Сила с которой действует заряд q3 на заряд q1: .

Пользуясь принципом суперпозиции получаем (это векторные величины нам необходимо использовать скалярные).

Модуль вектора F найдем по теории косинусов:



Из рисунка видна, что угол равен углу равностороннего треугольника = .

Подставляем числа



.

327. См. условие задачи 325. В п. 1 принять σ₁ = σ, σ₂= – 2σ. Β п. 2 принять σ = 20 нКл/м² и точку расположить справа от плоскостей.

Дано:

σ₁ = σ; σ₂= – 2σ; σ = 20 нКл/м^{2 .}

Найти:

E =?

Решение:

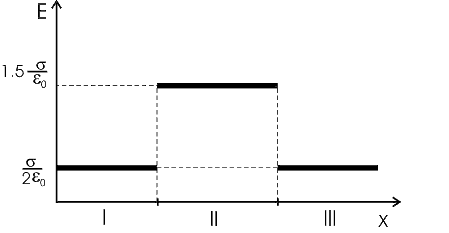
Воспользуемся принципом суперпозиции в каждой области.

В области I: E=E1-E2. Модуль , модуль , поэтому

. В этой области поле отлично от нуля.

В области II: E=E1+E2

В области III: E=E1-E2 . В этой области поле отлично от нуля.

---

Между плоскостями поле равно , и направлено влево.



337. Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью заряда τ = 800 нКл/м. Определить потенциал φ в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.

Дано:

R = 10 см; τ = 800 нКл/м; h = 10 см.

Найти:

φ =?

Решение:

Заряд всего кольца равен где τ-линейная плотность.

Потенциал от заряда в точке, отстоящей на расстоянии h от центра кольца, равен

Тогда полный потенциал равен



Подставляем числа



347. Какой минимальной скоростью _minдолжен обладать протон, чтобы он мог достигнуть поверхности заряженного до потенциала φ = 400 В металлического шара (рис. 29)?

Дано:

φ = 400 В.

Найти:

_min =?

Решение:





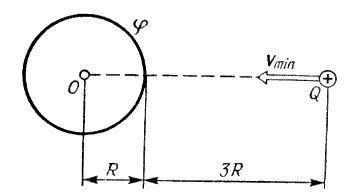
357. Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор подсоединен к источнику напряжения U = 80 В. Определить заряд Q и напряженность Е поля конденсатора в двух случаях: а) диэлектрик – воздух; б) диэлектрик – стекло.

Дано:

R = 10 см; d = 2 мм; U = 80 В;

Найти:


q1=?; q2=?; E1=?; E2=?

Решение:

Известно, что емкость плоского конденсатора

---

где -диэлектрическая проницаемость диэлектрика, d – расстояние между пластинами, S – площадь пластин, - электрическая постоянная.

С другой стороны известно C=q/U, где q – заряд на пластинах, U – приложенное напряжение.

Поэтому q=UxC=Ux

Откуда для имеем



Для имеем



Напряженность поля по определению равна E=U/d. Оно будет постоянно при любой среде между обкладками, если всегда поддерживается постоянная разность потенциалов U, поэтому E = 80В/0,002м=4х10⁴ В/м.

---

Смотрите также файлы

• Инклюзивное образование в условиях фгос на уроках математики дата.docx

• Тема. Технология проведения анализа и самоанализа урока (занятия, внеклассного, воспитательного мероприятия).docx

• Хронический лимфаденит лица и шеи. Аденофлегмона. Клиника, диагностика и принципы лечения. Проявления вичинфекции челюстнолицевой области.docx

• 1. День памяти о геноциде советского народа нацистами и их пособниками.docx

• Types of memory There are two main categories of memory longterm memory and shortterm memory. Most scientists believe there are at least four general types of memory working memory sensory memory shortterm memory longterm memory Working memory.docx