ТПР

Семинар

АЛГОРИТМ «ДИСКРИМИНАНТНАЯ ФУНКЦИЯ»
Назначение — решение задач распознавания в ситуациях, когда в материале обучения представлены объекты образов ( ), распределенные нормально в пространстве «объекты — свойства».

Постановка задачи. В исходных данных, представленных в виде ТОС, присутствуют представители всех образов. Для каждого объекта указана его принадлежность к образу. В процессе распознавания определяется принадлежность объектов экзамена к одному из образов.

Метод решения задачи. Этот метод основан на предположении, что объекты, составляющие каждый из образов, многомерно нормально распределены. Мы опираемся на эталонные объекты. Теоретически разделяются:

— линейный дискриминантный анализ, когда матрицы ковариации для разных образов равны;

— квадратичный дискриминантный анализ, когда матрицы ковариации для разных объектов различны.

Линейный дискриминантный анализ

Рассмотрим случай, когда в МО имеется два образа. Оказывается, что при равных ковариационных матрицах поверхностью, с одной стороны от которой больше вероятность принадлежности к одному из образов, а с другой к другому (критерий Байеса) является гиперплоскость, т. е. линейная поверхность размерности ( — размерность пространства). Уравнение гиперплоскости в общем виде можно записать следующим образом:

.

В данном случае эта поверхность вычисляется следующим образом:

(4.1)

Формула (4.1) называется уравнением линейной дискриминантной функции, где

---

— -мерный вектор столбец в пространстве свойств ;

— математическое ожидание (среднее) объектов 1-го образа;

— математическое ожидание (среднее) объектов 2-го образа;

— транспонирование;

— матрица коэффициентов ковариации.

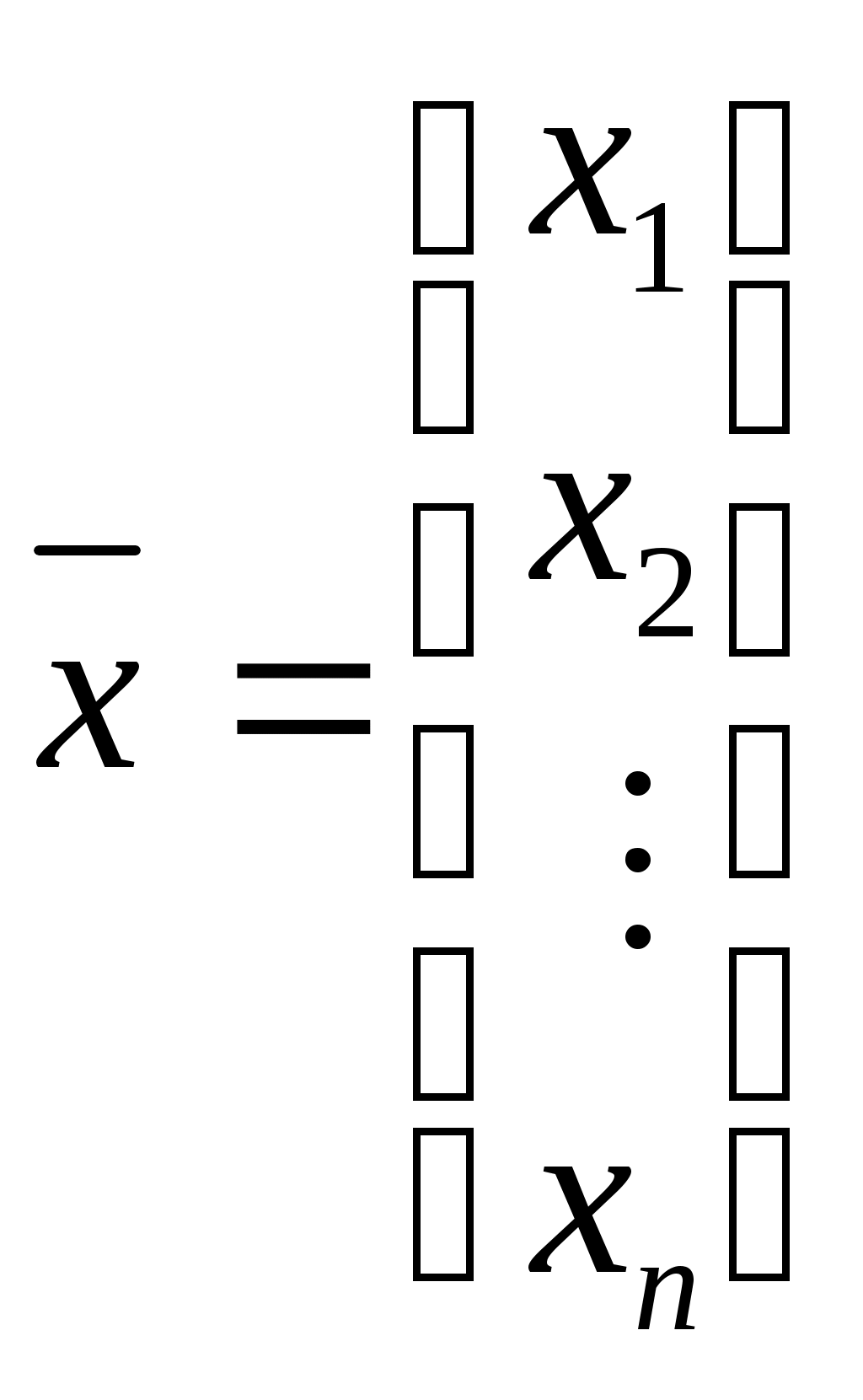Коэффициенты ковариации вычисляются следующим образом:

,

где m — математическое ожидание по к-ому свойству.

Коэффициенты ковариации тесно связаны с коэффициентом корреляции:

, где

— среднее квадратичное отклонение ( ) -го свойства;

— среднее квадратичное отклонение ( ) -го свойства;

Дисперсия .

Дискриминантная плоскость разбивает все пространство на две части. При этом точки пространства, относимые к 1-му образу, при подставлении своих координат в дискриминантную функцию дадут , а точки 2-го образа — .

Таким образом, подставляя координаты, интересующих нас объектов выборки, мы по дискриминантной функции определим, к какому из двух образов принадлежит объект (понятно, что с определенной долей вероятности). На рисунке (рис. 1) для двумерного случая это выглядит следующим образом:

---

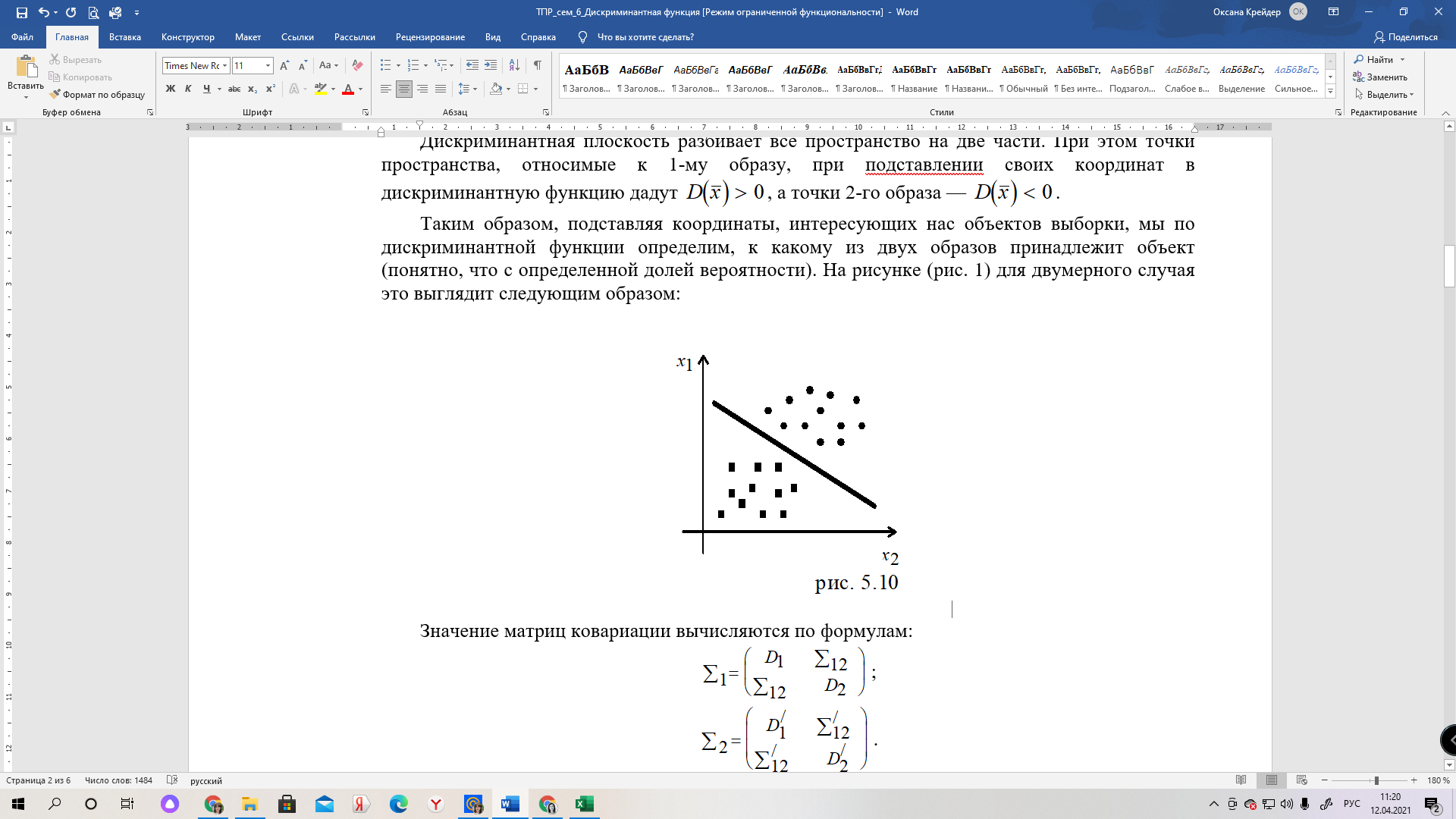
Рис.1.
Значение матриц ковариации вычисляются по формулам:

;

.

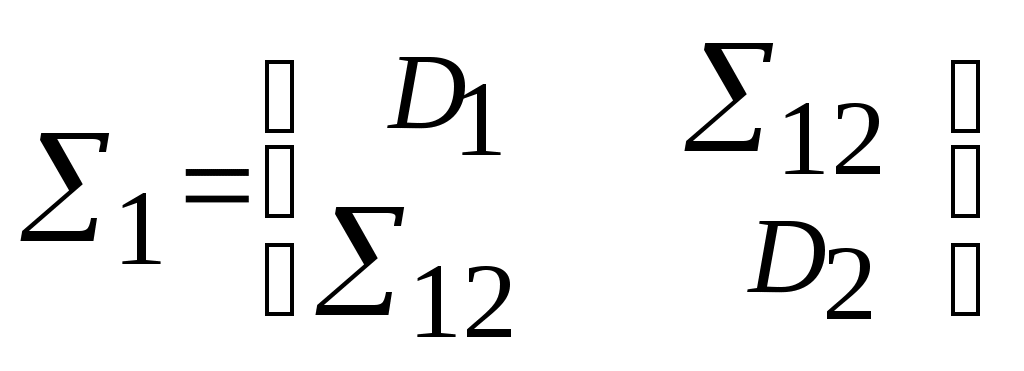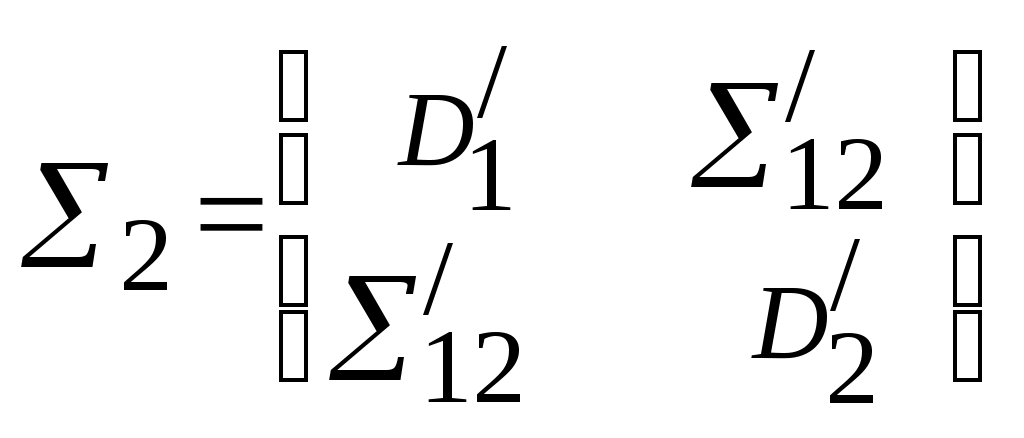Есть параметр, говорящий о качестве разбиения с помощью дискриминантной функции — это расстояние Махаланобиса:

.

Разбиение тем лучше, чем больше .
Квадратичный дискриминантный анализ

Был рассмотрен случай, когда матрицы ковариации для разных образов равны, и для распознавания использовалась линейная дискиминантная функция. Теперь рассмотрим ситуацию, когда матрицы ковариаций разных образов не совпадают. Для различных ковариационных матриц байесовский критерий предлагает строить квадратичную дискриминантную функцию. Однако, на практике ее строят чрезвычайно редко, поскольку никогда нельзя с точностью сказать равны или нет ковариационные матрицы. Мы ведь имеем только оценки, так как работаем не со всей генеральной совокупностью объектов, а только с выборкой из нее. Поэтому обычно вычисляют усредненную ковариационную матрицу для двух образов:

,

где

— число объектов в 1-ой выборке;

— число объектов во 2-ой выборке;

— ковариационная матрица для 1-го образа;

— ковариационная матрица для 2-го образа.

После этого применяется линейный дискриминантный анализ.

Распознавание с отказами. Пусть имеется образов, где

---

(т. е. известны эталоны для этих образов). Тогда можно построить линейную дискриминантную функцию для любой пары образов:

,

где , j =1, — образы. относится к -му образу, если для всех , или к области отказа, если такового — нет.

Посмотрим, как это выглядит на графике (рис. 4.11), где

D — гиперплоскости;

1, 2, 3 — образы;

4 — область отказа.

В область отказа попадают такие точки, для которых невозможно определить принадлежность к одному из образов. Другими словами, точка отказа — это такая точка, координаты которой при подставлении в дискриминантную функцию дают следующие значения:

;

;

;

.

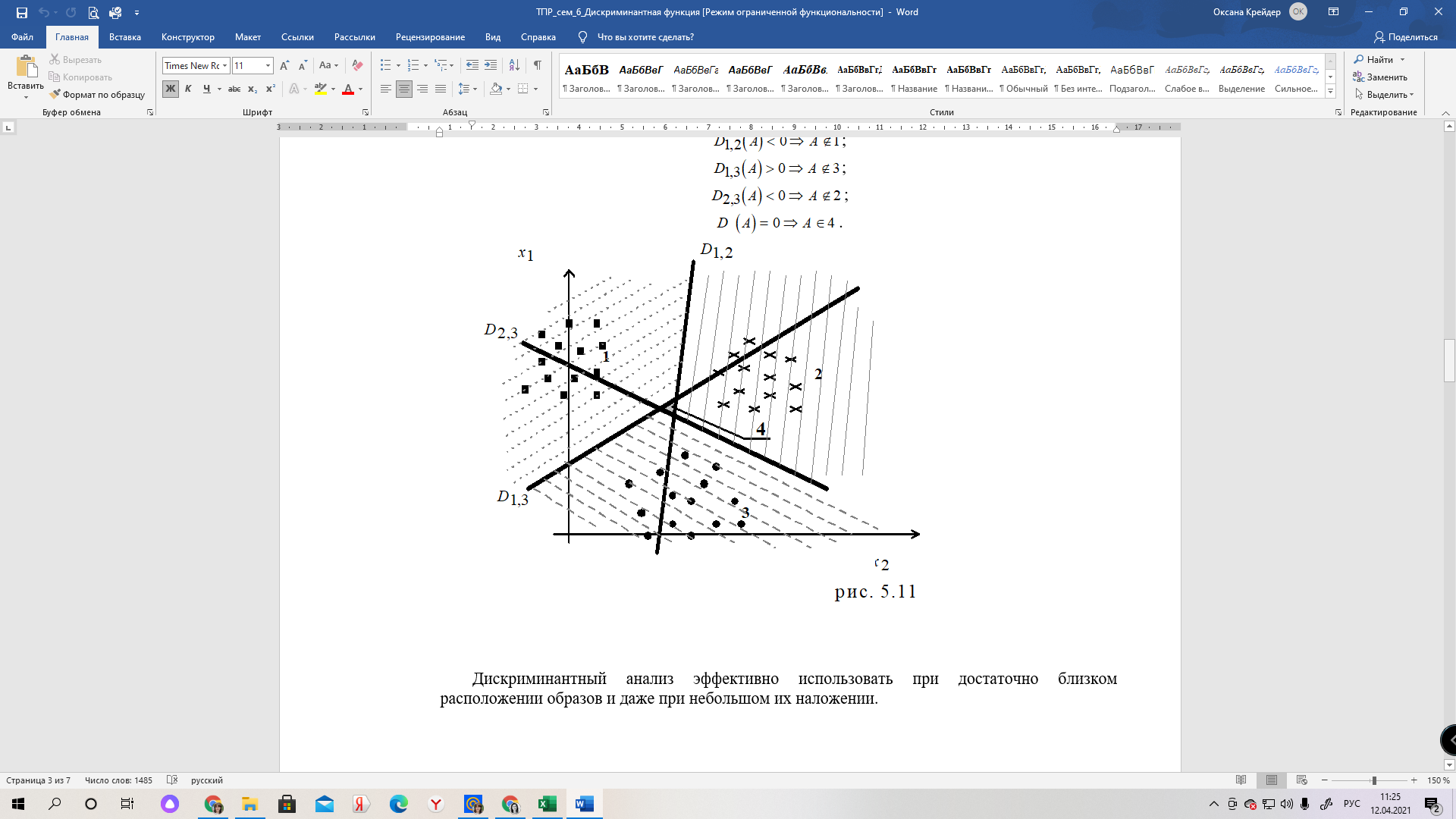Рис.2.
Дискриминантный анализ эффективно использовать при достаточно близком расположении образов и даже при небольшом их наложении.


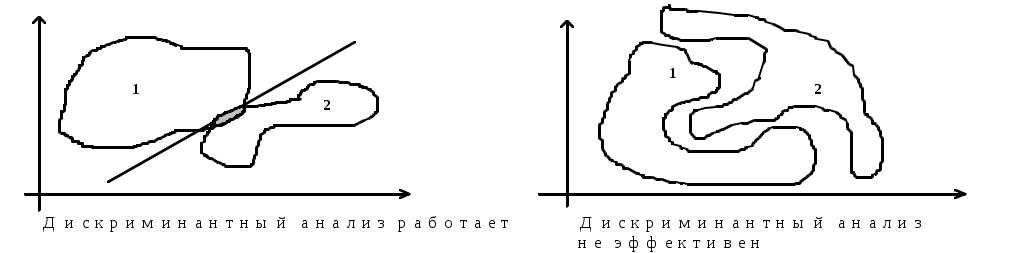
Рис.3.

Практика показала, что дискриминантный анализ хорошо работает и для случая, когда нет многомерного нормального распределения. При этом необходимо, чтобы распределение по каждому образу было все-таки симметрично и унимодально. Правда, при этом алгоритм уже нельзя рассматривать как статистический, а можно говорить об эвристическом алгоритме распознавания образов.
П р и м е р.

---

После отбора в модельном агентстве девушек делят на две группы: для Модельера№1 и для Модельера№2. Распределение происходит при условии, что для Модельера№1 необходимы девушки с объемом талии 50—60 см и весом от 40—50 кг, а для Модельера№2 требуются девушки с объемом талии 60—70 см и весом 50—60 кг.

Таким образом, мы имеем два образа: Модельер№1 и Модельер№2. Для каждого образа измерены два свойства: объем талии и вес. Нам известна часть представителей из этих образов и значение их свойств (табл. 2). Требуется отнести объекты МЭ к одному из образов.

Табл.2

---

Смотрите также файлы

• Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Менеджмент.docx

• Пп Критерии анализа Содержательные характеристики.docx

• Исследовательская работа по теме Внешняя политика Екатерины ii кирпичики величия России.doc

• 2саба Сабаты таырыбы Жазытытаы нктені координаталары. Екі нктені араашытыы. Кесінді ортасыны координатасы.docx

• Учебной работе Кобландина К. С. 2022 г. Календарно тематический план педагога для организации технического и профессионального, послесреднего образования.docx