Лабораторная работа № 7
Создание макросов в Excel
Цель работы: Ознакомиться со способами создания и использования макросов.

Задание на выполнение работы: создать макросы с использованием Excel

Порядок выполнения работы:
Вариант 20

Дана следующая матрица выигрышей:



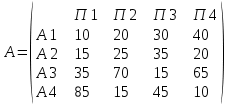
Определите оптимальную стратегию используя критерии Вальда, Сэвиджа и Гурвица (коэффициент пессимизма равен 0,5).



Решение:

Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) A_i, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(a_ijp_j)
∑(a_1,jp_j) = 10*0.25 + 20*0.25 + 30*0.25 + 40*0.25 = 25
∑(a_2,jp_j) = 15*0.25 + 25*0.25 + 35*0.25 + 20*0.25 = 23.75
∑(a_3,jp_j) = 37*0.25 + 70*0.25 + 15*0.25 + 65*0.25 = 46.75
∑(a_4,jp_j) = 85*0.25 + 15*0.25 + 45*0.25 + 10*0.25 = 38.75

Ai	П1	П2	П3	П4	∑(aijpj)
A1	2.5	5	7.5	10	25
A2	3.75	6.25	8.75	5	23.75
A3	9.25	17.5	3.75	16.25	46.75
A4	21.25	3.75	11.25	2.5	38.75
pj	0.25	0.25	0.25	0.25

---

Выбираем из (25; 23.75; 46.75; 38.75) максимальный элемент max=46.75
Вывод: выбираем стратегию N=3.
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min a_ij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

Ai	П1	П2	П3	П4	min(aij)
A1	10	20	30	40	10
A2	15	25	35	20	15
A3	37	70	15	65	15
A4	85	15	45	10	10

Выбираем из (10; 15; 15; 10) максимальный элемент max=15
Вывод: выбираем стратегию N=2.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max r_ij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.

---

1. Рассчитываем 1-й столбец матрицы рисков.
r₁₁ = 85 - 10 = 75; r₂₁ = 85 - 15 = 70; r₃₁ = 85 - 37 = 48; r₄₁ = 85 - 85 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r₁₂ = 70 - 20 = 50; r₂₂ = 70 - 25 = 45; r₃₂ = 70 - 70 = 0; r₄₂ = 70 - 15 = 55;
3. Рассчитываем 3-й столбец матрицы рисков.
r₁₃ = 45 - 30 = 15; r₂₃ = 45 - 35 = 10; r₃₃ = 45 - 15 = 30; r₄₃ = 45 - 45 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r₁₄ = 65 - 40 = 25; r₂₄ = 65 - 20 = 45; r₃₄ = 65 - 65 = 0; r₄₄ = 65 - 10 = 55;

Ai	П1	П2	П3	П4
A1	75	50	15	25
A2	70	45	10	45
A3	48	0	30	0
A4	0	55	0	55

Результаты вычислений оформим в виде таблицы.

Ai	П1	П2	П3	П4	max(aij)
A1	75	50	15	25	75
A2	70	45	10	45	70
A3	48	0	30	0	48
A4	0	55	0	55	55

---

Выбираем из (75; 70; 48; 55) минимальный элемент min=48
Вывод: выбираем стратегию N=3.
Проведение идеального эксперимента.
В крайнем правом столбце рассчитаем средний риск.

					ri
					0
					0
					0
					0

Минимальное значение средних рисков равно 0. Следовательно, выше этой цены планирование эксперимента становится нецелесообразным.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(s_i)
где s_i = y min(a_ij) + (1-y)max(a_ij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем s_i.
s

---

₁ = 0.5*10+(1-0.5)*40 = 25
s₂ = 0.5*15+(1-0.5)*35 = 25
s₃ = 0.5*15+(1-0.5)*70 = 42.5
s₄ = 0.5*10+(1-0.5)*85 = 47.5

Ai	П1	П2	П3	П4	min(aij)	max(aij)	y min(aij) + (1-y)max(aij)
A1	10	20	30	40	10	40	25
A2	15	25	35	20	15	35	25
A3	37	70	15	65	15	70	42.5
A4	85	15	45	10	10	85	47.5

Выбираем из (25; 25; 42.5; 47.5) максимальный элемент max=47.5
Вывод: выбираем стратегию N=4.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₃.
Множество Парето

E1	10	20	30	40
p	0.25	0.25	0.25	0.25

ME(1)=10*0.25+20*0.25+30*0.25+40*0.25=25=25
σ(1)=sqrt(10²*0.25+20²*0.25+30²*0.25+40²*0.25-25²) = sqrt(125)=11.18

---

Смотрите также файлы

• Темы рефератов 2 семестр.pdf

• Решение внп (по расходам) Расходы на личное потребление Валовые инвестиции Госзакупки товаров и услуг Экспорт Импорт 325 76 105 57 10 553.docx

• Подобрать фото и иллюстрации.docx

• Задача Определить коэффициент сменности, если дано в механическом цехе установлено 20 единиц оборудования, из них 12 токарные станки, 8 фрезерные..pdf

• Цель получить практические навыки проведения оценки риска и возникновения чрезвычайных ситуаций, вредных и нежелательных явлений.pdf