Порядок вычисления:

1. Составить расчетную таблицу.

2. Вычислить коэффициент корреляции и уравнение регрессии.

3. Построить график зависимости величины ошибки ∆ от длины линии D.

4. Сделать вывод.

Решение:

1. Составим таблицу:

	D, км	, мм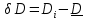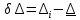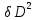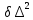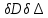
1
2
3
…
16
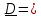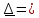			Σ =	Σ =	Σ =	Σ =	Σ =

2. Вычислим коэффициент корреляции:



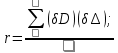
Найдем средние квадратические ошибки m_D и m_∆:



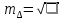
Определим надежность коэффициента корреляции (по таблице):

см. приложение Г «Значение функции Z», приняв коэффициент корреляции в качестве аргумента.

---

Найдем надежностный интервал для z:

z - t·G_Z ≤ z ≤ z + t·G_Z

По условию задачи t=2;


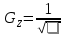
Минимально допустимое значение коэффициента корреляции вычислим по формуле:



.

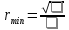
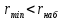Составим уравнение регрессии:

.

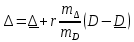3. Построим график зависимости величины ошибки ∆ от длины линии D и прямую по уравнению регрессии.

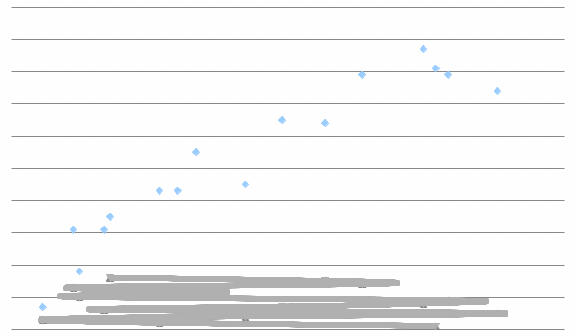
4. На основании полученных данных (по виду графика и неравенств) можно ли считать корреляционную связь установленной.

Лабораторная работа №3

Обработка результатов равноточных измерений одной величины

Цель работы: обработать данный ряд равноточных измерений.

Дано: даны результаты равноточных измерений линии (м):

110, 338

381

394

387

385

379

393

386

382

389
Порядок выполнения работы:

1.Составить расчетную таблицу.

2. Провести контроль для суммы уклонений.

3. Вычислить и провести контроль величины .

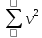4. Вычислить среднюю квадратическую ошибку отдельного измерения.

5.Определить надежность средней квадратической ошибки отдельного результата измерений.

6.Вычислить среднюю квадратическую ошибку среднего арифметического.

7. Определить надежность средней квадратической ошибки среднего арифметического.

Решение:

1. 
   Составим расчетную таблицу.
   

i	Li, м	ε=li – l0		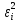νi, мм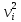
1
2
3
Σ	-

---

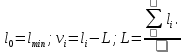
2. Контроль для суммы уклонений:



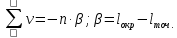
3. Вычислим и проведем контроль величины :



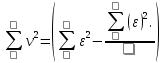
4.Вычислим среднюю квадратическую ошибку отдельного измерения по формуле Бесселя:



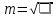
5.Определим надежность средней квадратической ошибки отдельного результата измерений:



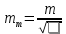
6.Вычислим среднюю квадратическую ошибку среднего арифметического:



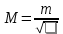
7.Определим надежность средней квадратической ошибки среднего арифметического:



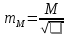
Лабораторная работа №4

Оценка точности по разностям двойных равноточных измерений

Цель работы: оценить точность двойных равноточных измерений по их разностям.

Дано: даны превышения между точками, определенные по черной и красной сторонам реек.

Порядок выполнения работы:

1. Составить расчетную таблицу.

2. Провести контроль значения .

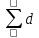3. Вычислить среднюю квадратическую ошибку одного измерения и среднюю квадратическую ошибку арифметической середины.

4. Определить надежность средней квадратической ошибки отдельного результата измерений.

5. Определить надежность средней квадратической ошибки среднего арифметического.

Решение:

1.Составим расчетную таблицу:

№ превышений				Превышения, вычисленные по сторонам реек:						d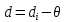,мм	, мм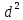
				черная			красная
1				+1,384			+1,382
2				-0,817			-0,813
3				+0,373			+0,370
4				+0,448			+0,451
5			+1,755			+1,758
6			+0,211			+0,215
7			+0,314			+0,317
8			-0,227			-0,229
9		+0,972				+0,975
Σ	-				-

---

Вычислим значение остаточной систематической ошибки θ:


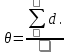
2. Контроль значения


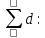
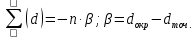
Критерием допустимости 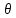является неравенство: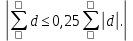



3. Вычислим среднюю квадратическую ошибку одного измерения :



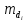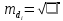
Вычислим среднюю квадратическую ошибку арифметической середины :



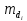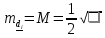
Следует заметить, что средние квадратические ошибки, полученные по разностям двойных измерений, обычно дают преуменьшенные результаты.

4. Определим надежность средней квадратической ошибки отдельного результата измерений:



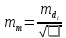
5. Определим надежность средней квадратической ошибки среднего арифметического:



Лабораторная работа №5

«Обработка ряда неравноточных измерений»

Теоретические пояснения

---

Обратный вес функции общего вида

Пусть дана функция 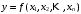  , где 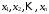 — независимо измеренные величины. Известны их веса .

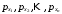Используя формулы средней квадратической ошибки функции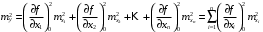

 и веса 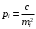, получаем следующую формулу для вычисления обратного веса функции: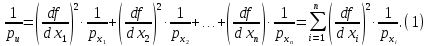



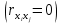- условие.

Если величины 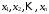коррелированы, т.е. коэффициенты попарной корреляционной связи отличны от нуля, 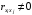, то обратный вес функции вычисляется по формуле: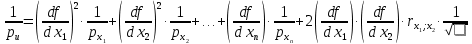



Положим, что при измерении величины х получены равноточные значения:

a₁, a₂, …, a_k

b₁,b₂, …, b_q

c₁, c₂, …, c_n

Вероятнейшим, т.е. более надежным значением х является средняя арифметическая середина:





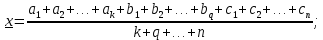
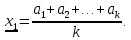
Используя формулу (2), получим:





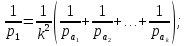
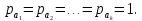
С учетом этих значений находим формулу общей арифметической середины:











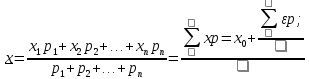
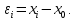
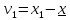
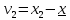
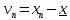
Умножив левые и правые части этих выражений на веса измерений и после сложения получим:

---

Смотрите также файлы

• Групповое занятие по дисциплине Раздел 3 Огневая подготовка из стрелкового оружия Тема 14 Основы, приёмы и правила стрельбы из стрелкового оружия. Занятие 1.pptx

• Рекламное сообщение.pptx

• Письменное задания.docx

• Планконспект проведения учебного занятия по овп. 03 с 22 учебным взводом.docx

• Выбор и расчет средств комплексной механизации очистного забоя курсовой проект.docx