Файл: Подготовка данных к статистической обработке.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 21

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическая работа 1

Тема: Подготовка данных к статистической обработке

Задание 1 Браковка сомнительных данных
Сомнительные данные, которые значительно отличаются от всех остальных данных, определяются только с помощью математической статистики. Субъективная браковка данных недопустима.

С помощью математической статистики определить достоверность и забраковать сомнительные данные эксперимента.

Ход анализа:

Чтобы убедиться, что все данные принадлежат к определенному вариационному ряду, выполняются следующие операции:

  1. Ранжируют вариационный ряд в возрастающем порядке. Двум первым данным присваивают обозначения х1 и х2, а двум последним хn и хn-1. Наиболее сомнительными будут крайние. Их сомнительность проверяется путем расчёта критерия τ (тау) для х1 и хn по формулам:

  1. проверка сомнительности первого числа

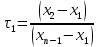, где τ1 – фактическое значение критерия τ для первого числа

  1. проверка сомнительности последнего числа

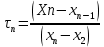, где τn – фактическое значение критерия τ для последнего числа

  1. Находят значения теоретического критерия τ (τ01 или τ05) по объёму выборки (n) (приложение1).

  2. Сравнивают расчётные критерии с теоретическим: если расчётные больше или равны теоретическому, то проверяемые данные сомнительны. На основании проведенных расчётов делают выводы о сомнительности или достоверности проверяемых данных.


Варианты задания

1.
22,3
21,9
15,6
22,5
27,8
21,5
21,6
23,4



2.
5,7
6,8
5,9
6,6
1,2
5,5
5,6






3.
12,5
10,6
12,3
12,5
12,4
12,2
12,1
20,0



4.
1,9
2,0
2,0
1,9
0,3
2,1
2,0






5.
37,0
51,5
43,8
50,2
38,6
29,0
43,5






6.
32,0
33,2
12,5
41,3
40,0
31,0









7.
10,0
12,2
16,3
11,4
18,5
12,6
7,1
21,8



8.
16,25
12,54
15,36
14,56
16,44
13,06
5,03






9.
1,97
2,23
2,01
2,56
2,20
2,12









10.
12,5
12,3
12,6
12,4
12,6
12,2
12,7






11.
72
7,5
74
70
79
78
73






12.
10,8
10,7
9,8
10,7
10,4
11,4









13.
1,20
1,64
1,39
1,42
1,40
1,01
1,40
1,24



14.
152
67
130
132
136
107
131
97
117

15.
22,2
21,3
19,8
18,7
15,6
20,1
22,4







Приложение 1

Значение критерия τ для 5-% уровня значимости

n
τ
n
τ

4
0,995
13
0,395

5
0,807
16
0,369

6
0,689
18
0,349

7
0,610
20
0,334

8
0,554
22
0,320

9
0,512
24
0,309

10
0,477
26
0,299

11
0,460
28
0,291

12
0,428
30
0,283


Задание 2 Восстановление выпавших данных

Обработка данных часто осложняется выпадение данных на некоторых участках (делянках) эксперимента (повреждение растений птицами, вредителями, затопление после ливней, проезд транспорта и т.д.). Из-за выпадения средние арифметические в вариантах могут быть либо завышены, если выпала дата с низким числовым значением, либо занижены, если выпала дата с наибольшим числовым значением. В результате возникают ошибки, которые можно устранить, если выпавшие данные восстановить, т.е. вычислить их наиболее вероятностные значения.

С помощью математической статистики восстановить выпавшие в эксперименте данные, сделать вывод.
Ход анализа:

При выпадении одного результата пользуются формулой:

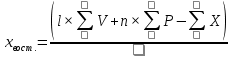, где

l
- число вариантов;



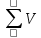- сумма данных в варианте, где выпал результат;

n
- число повторений в эксперименте;



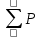- сумма данных в повторении, где выпал результат;



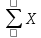- сумма данных во всем эксперимента, за исключением выпавшего результата.


Восстановленный результат ставят на выпавшее место и выполняют соответствующей анализ.

Варианты задания

1.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V
VI




15,8
12,9
15,3
16,0
17,9
16,0




16,2
16,1
15,8
16,3
15,3
17,8




17,8
15,0
*
16,3
16,0
18,1

2.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V




9,7
10,4
14,5
14,4
12,9




10,0
9,9
9,8
13,2
10,5




10,2
*
9,6
11,2
12,4




10,3
10,8
10,8
9,9
13,5

3.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V
VI




221,3
229,3
223,6
291,2
231,5
231,5




228,9
192,0
202,2
192,0
*
222,5




262,7
232,4
221,5
222,5
250,1
231,5

4.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV




21,3
24,3
23,0
20,9




21,3
21,5
22,2
21,3




24,3
20,8
23,1
*




21,1
20,9
21,9
21,3




23,2
21,5
20,5
20,9


5.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V




860,0
870,4
860,3
850,2
958,5




840,2
841,2
838,9
*
880,1




960,3
962,2
839,9
958,5
802,3


6.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V




860,0
870,4
860,3
850,2
958,5




840,2
841,2
838,9
*
880,1




960,3
962,2
839,9
958,5
802,3




880,2
878,2
882,2
880,1
817,1


7.

Варианты
Экспериментальные данные по повторениям

I
II
III
IV
V
VI




5,6
3,4
6,8
7,2
5,5
9,0




4,0
4,6
6,5
8,1
6,8
5,6




5,9
8,7
6,5
8,0
8,6
*

Смотрите также файлы