№	Задания
1	Углы вы­пук­ло­го че­ты­рех­уголь­ни­ка от­но­сят­ся как 1:2:3:4. Най­ди­те мень­ший угол. Ответ дайте в градусах.
2	Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 115°.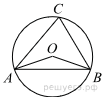
3	Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.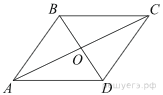
4	На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.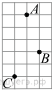
5	Какие из следующих утверждений верны? Доказать!   1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8. 2) Любые два равнобедренных треугольника подобны. 3) Любые два прямоугольных треугольника подобны. 4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.   Если утверждений несколько, запишите их номера в порядке возрастания.
6	Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
7	Найдите тангенс угла В треугольника ABC, изображённого на рисунке.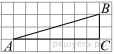

Ответы:

1. 
   36
   
2. 
   57,5
   
3. 
   2400
   
4. 
   4
   
5. 
   1
   
6. 
   6
   
7. 
   3,5
   

Решение:

1. Пусть x — меньший угол четырехугольника, тогда другие его углы равны 2

---

х, 3х и 4х. Так как сумма углов выпуклого четырехугольника равна 360° имеем:

 



 

Таким образом, меньший угол четырёхугольника равен 36°.

 

Ответ: 36.

2. Угол ACB − вписанный угол, он равен половине центрального угла, опирающегося на ту же дугу. Т. е. 

 

Ответ: 57,5.

3. Введём обозначения, как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть АС=80. Рассмотрим треугольник АВО он прямоугольный, из теоремы Пифагора найдём ВО:
 

 

Найдём площадь ромба как половину произведения его диагоналей:

 



 

Ответ: 2400.

4. Расстояние от точки А до середины отрезка ВС равно четырём сторонам клетки, или 4 см.

 

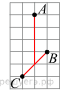
Ответ: 4.

5. Проверим каждое из утверждений.

1) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.»— верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

2) «Любые два равнобедренных треугольника подобны.» — неверно, так как углы, заключенные между пропорциональными сторонами, не равны.

3) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.

4) «Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.» — неверно, треугольник с такими сторонами является прямоугольным.

 

Ответ: 1.

6. Пусть сторона ромба равна a, тогда




 

Ответ: 6.

7. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

---

Ответ: 3,5.

---

Смотрите также файлы

• Рабочая программа Подготовка детей к школе.docx

• Этап Содержание Переживания приемного родителя Поведение приемного ребенка.pdf

• Контрольная работа по праву. 11 класс I. Объяснить значение следующих терминов.docx

• Описание деятельности Перед мэрией города районного значения НьюВасюки.doc

• Отчет о прохождении учебной практики (по получению первичных профессиональных умений и навыков) Эренценовой Алтын Убушаевны.docx