Файл: Контрольная работа по дисциплине Анализ данных Вариант 7 Найдем количество не выученных вопросов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра "Менеджмент, информатика и общегуманитарные науки"
Контрольная работа
по дисциплине
«Анализ данных»
Вариант 7
1.
Найдем количество не выученных вопросов:
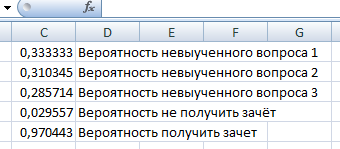
30 - 20 = 10.
Тогда вероятность выбора такого вопроса, составит:
10 : 30 = 0,333333333
Вероятность, что ему повторно попадется не выученный вопрос составит:
=(10-1)/(30-1)
Вероятность, что ему повторно попадется не выученный вопрос составит:
=(9-1)/(29-1)
Общая вероятность такого события равна произведению вероятностей:
=C1*C2*C3= 0,02955665
Тогда вероятность получить зачет равна:
=1-C4= 0,97044335
Ответ: вероятность получения зачета составляет 0,97044335
2.
Решение.
Событие A = {студент в итоге соревнования попал в сборную}.
Можно сделать 3 предположения:
H1H1 = {студент принадлежал 1-й группе}.
H2H2 = {студент принадлежал 2-й группе}.
H3H3 = {студент принадлежал 3-й группе}.
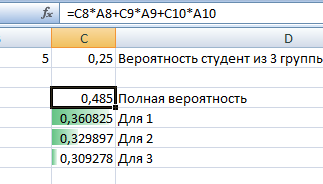
Условная вероятность того, что студент в итоге соревнования попал в сборную, при условии, что верно предположение H1H1, равна
PH1(A)= PH1(A)=0,35
Условная вероятность того, что студент в итоге соревнования попал в сборную, при условии, что верно предположение H2H2, равна
PH1(A)= PH1(A)=0,4
Условная вероятность того, что студент в итоге соревнования попал в сборную, при условии, что верно предположение H3H3, равна
PH3(A)= (A)=0,25
Рассчитаем полную вероятность
Далее рассчитаем благоприятные события для каждого из групп по формуле Байеса
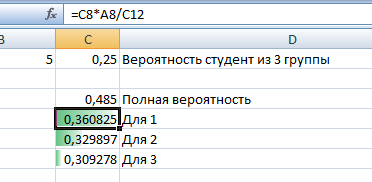Из этого следует, что вероятнее всего в сборною попадет студент из 1 группы.3.
Для начала рассчитаем вероятность НЕ получить дивиденды
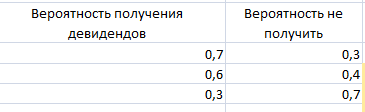Для этого из 1 нужно вычесть вероятность получения дивидендов.Затем рассчитаем все варианты получения дивидендов путем перебора.
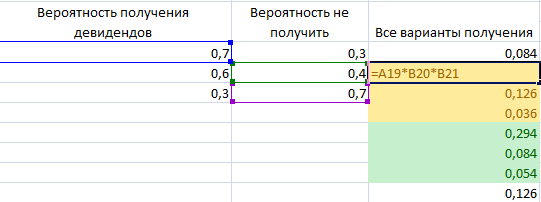
Затем построим закон распределения
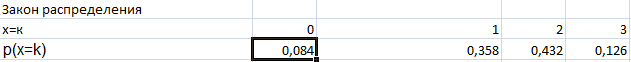
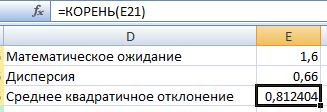
Затем исходя из закона распределение рассчитаем математическое ожидание и дисперсию
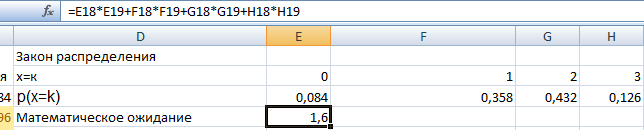
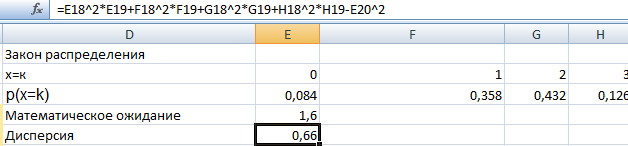
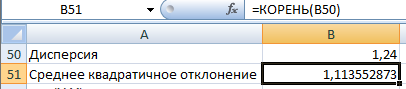
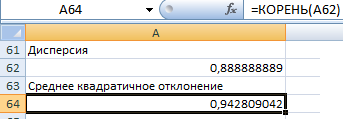
Затем найдем среднее квадратичное отклонение, для этого используем функцию вычисления квадратного корня из дисперсии
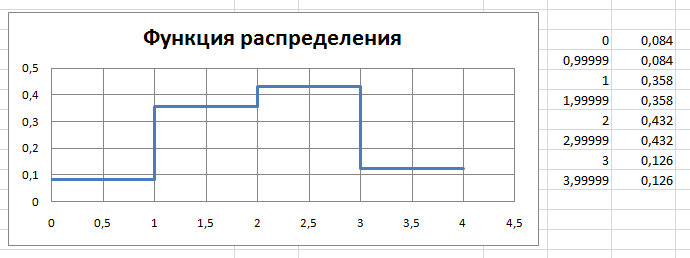
Затем по данным построим функцию распределения
4.
По условию у нас даны условные величины, которые справедливы для переменных Х и У.
Рассчитаем математическое ожидание используя формулу для Z.
Далее исходя из этой формулы также рассчитаем дисперсию :
5.
Рассчитаем математическое ожидание для Х и У.
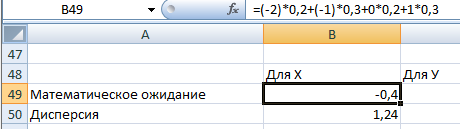
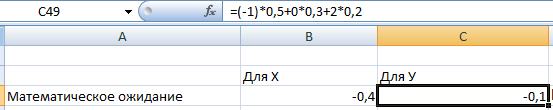
Далее рассчитаем дисперсию для этих переменных
Затем рассчитаем среднее квадратичное отклонение от каждой из величин дисперсии
Они понадобятся нам для вычисления ковариации
Затем рассчитаем коэффициент ковариации, для этого мы значение ковариации разделим на произведение средних квадратичных отклонений
Поскольку, P(X=-2,Y=-1) = 0.1=0.2•0.5, то случайные величины X и Y независимы.
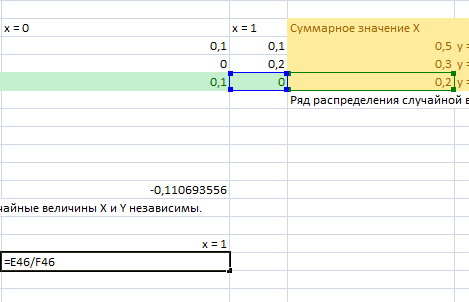
Составим Ряд распределения случайной величины У
Для того нам нужно сложить все величины Х соответствующие ряду У.Для того чтобы составить Ряд распределения случайной величины Х, нужно каждое значение Х справедливое для у=2 разделить на значение суммарного ряда у=2
6.
А)Случайная величина Х задана плотностью распределения f(x):
Б)
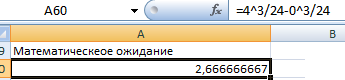
В)Найдем математическое ожидание исходя из интегрального выражения функции
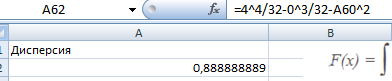
Далее найдем дисперсию
После найдем среднее квадратичное отклонение ,используя функцию КОРЕНЬ из дисперсии
Г)
