Файл: Отчет по лабораторной работе отправить преподавателю по электронной почте.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 18

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Индивидуальное задание по лабораторной работе
Расчет линейной регрессивной зависимости функции от фактора

Расчет регрессивной зависимости функции у от фактора х рассмотрим на примере. Цель работы – определить уравнение линейной зависимости функции от фактора.

Исходные данные в виде статистического ряда парных измерений приведены в табл. 1. Из выборки исходных данных исключены грубые ошибки измерений. Измерения удовлетворяют условиям воспроизводимости эксперимента.


Отчет по лабораторной работе представить в следующем виде: значение коэффициента корреляции r; уравнение линейной регрессии с цифровыми значениями коэффициентов; график зависимости у от фактора х .

Отчет по лабораторной работе отправить преподавателю по электронной почте.

Таблица 1

Статический ряд парных измерений фактора и функции





Вариант

1

Фактор х
1
2
3
4
5
6
7
8

Функция у
1
4
6,9
9
10,8
12
14
16

2
х
5
6
7
8
9
10
11
12

у
10,8
12
14
16
19
20,1
23
23,4

3
х
9
10
11
12
13
14
15
16

у
19
20,8
23
23,4
27
28,1
31
32

4
х
13
14
15
16
17
18
19
20

у
27
28,1
31
32
35,4
40
39,1
40,1

5
х
17
18
19
20
21
22
23
24

у
35,5
40
39,1
40,1
45
47,9
51
52

6
х
21
22
23
24
25
26
27
28

у
45
47,9
51
52
54,9
55,8
59
58,7

7
х
25
26
27
28
29
30
31
32

у
54,9
55,8
59
58,7
63,5
65,4
69,7
72,6

8
х
29
30
31
32
33
34
35
36

у
63,5
65,4
69,7
72,6
74,9
79
80
83,8

9
х
33
34
35
36
37
38
39
40

у
74,9
79
80
83,8
85,5
87,6
88,9
91,2

10
х
37
38
39
40
41
42
43
44

у
85,5
87,6
88,9
91,2
92,9
96
98,9
101

11
х
41
42
43
44
45
46
47
48

у
92,9
96
98,9
101
103
106,4
107,9
112,4

12
х
45
46
47
48
49
50
51
52

у
103
106,4
107,9
112,4
114,8
118,7
121,7
127,6

13
х
49
50
51
52
53
54
55
56

у
114,8
118,7
121,7
127,6
98,9
131,3
133
137,3

14
х
53
54
55
56
57
58
59
60

у
98,9
131,3
133
137,3
139
140,1
144
144,2

15
х
9
10
11
12
13
14
15
16

у
19
20,1
23
23,4
27
28,1
31
32

16
х
17
18
19
20
21
22
23
24

у
35,4
40
39,1
40
45
47,9
51
52

17
х
25
26
27
28
29
30
31
32

у
54,9
55,8
59
58,7
63,5
65,4
69,7
72,6


Производим промежуточные вычисления для уравнения линейной регрессии, результаты расчетов сводим в табл. 2.

Определяем среднее арифметическое значение для факторов хi по формуле

. (1)

Коэффициент линейной корреляции r может принимать значения от –1 до +1. При r = 0 линейная корреляционная связь между х и у отсутствует, при r = 1 существует строгая функциональная линейная связь х и у. Если | r | 0,5, то принято считать, что между фактором х и функцией отклика у имеется линейная корреляционная связь.

Определяем среднее арифметическое значение функции отклика по формуле (1)

. (2)

Определяем коэффициент линейной корреляции по формуле

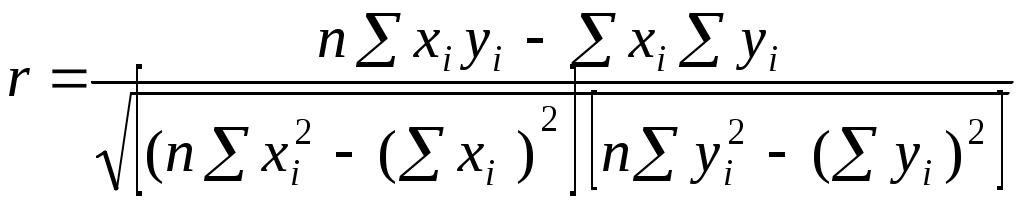. (3)

Таблица 2

Значения промежуточных величин для уравнения регрессии


хi
уi

хi2
хi2
хi уi

2
4,01
4
16,08
8,02

6
12,01
36
144,24
72,06

10
20,18
100
407,23
201,80

14
28,09
196
789,05
393,26

18
39,95
324
1596,00
719,10

22
47,90
484
2294,41
1053,80

26
55,85
676
3119,22
1452,10

27
58,93
729
3472,74
1591,11

28
58,71
784
3446,86
1643,88

32
72,59
1024
5269,31
2322,88

36
83,80
1296
7022,44
3016,8

40
91,22
1600
8321,09
3648,8

44
101,07
1936
10215,14
4447,08

45
102,90
2025
10588,41
4630,50

46
106,40
2116
11320,96
4894,40

50
116,69
2500
13616,56
5834,50

54
131,90
2916
17397,61
7122,60

72
178,49
5184
31858,68
12851,28

76
190,20
5776
36176,04
14455,20

77
192,20
5929
36940,84
14799,40

78
195,09
6084
38060,11
15217,02

82
207,19
6724
42927,70
16989,58

86
222
7396
49284
19092

104
261
10816
68121
27144

Σхi =1075
Σуi = 2578,37
Σхi2 = 66655
Σуi 2 = 402405,727
Σ(хi уi) = 163601,17


Определяем значение постоянных коэффициентов a, b уравнения линейной регрессии y = a + bx :

расчетный тангенс угла наклона линии регрессии
b = ;

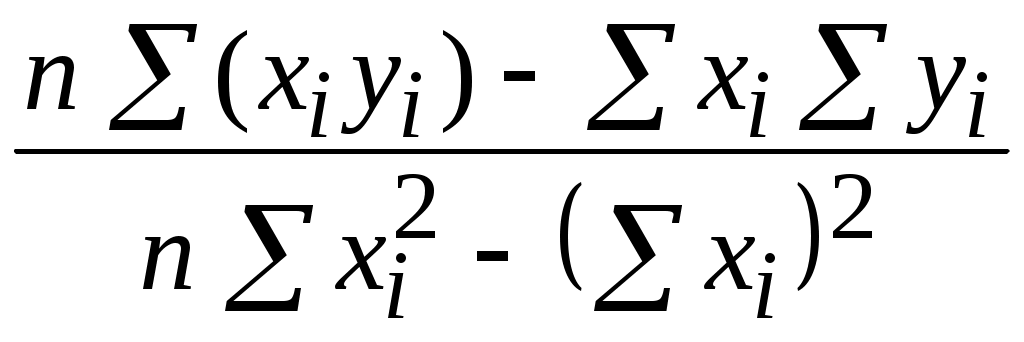расчетное значение свободного члена

а = .

После подстановки значений коэффициентов а и b уравнение линейной регрессии примет вид y = aр + bрx .

Графическая зависимость уот х приведена на рис. 1.

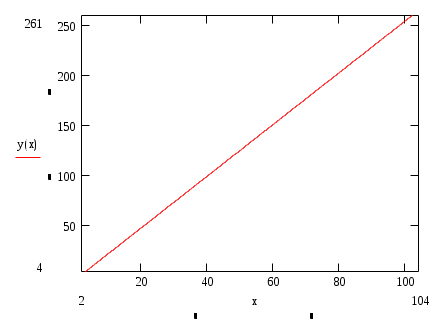
Рис. 1. График зависимости y от фактора x
Определяем коэффициент детерминации, который отражает влияние фактора х на функцию у. КД = r2. Например при КД = 0,997 функция у на 99,7 % зависит от фактора х и лишь на 0,03 % от других причин.

При r < 0,5 линейная корреляционная связь между фактором х и функцией отклика у считают неудовлетворительной. В этом случае степень влияния переменных друг на друга может изменяться непрямолинейно. Для определения связи между х и у в виде плавных кривых линий применяются методы подбора эмпирических формул.
Индивидуальное задание к практическому занятию
Подбор эмпирических формул для однофакторного эксперимента по

методу средних квадратов

Расчет эмпирических формул для однофакторного эксперимента по методу средних квадратов выполнить по своему варианту статистического ряда парных измерений (см. выше задание к лабораторной работе).

Цель – изучить метод средних квадратов для подбора эмпирических формул по данным однофакторного эксперимента.

Задачи – составить полиноминальное уравнение; составить систему начальных уравнений для расчета коэффициентов полинома; рассчитать коэффициенты полиноминального уравнения, записать уравнение полинома и построить график полиноминальной зависимости функции у от фактора х.

Методика расчета эмпирических формул для однофакторного эксперимента
по методу средних квадратов приведена в методических указаниях: Сиваков В,П. «Модель и метод факторного эксперимента» на стр. 13-16, а также в учебном пособии: Сиваков В.П., Вураско А.В. Леонович А.А. Основы научных исследований в химической и химико-механической переработке сырья растительного происхождения : учеб. пособие. – Екатеринбург : УГЛТУ. 2021. – 168 с. (см. стр. 110-113).

Отчет по практическому занятию представить в виде полиноминального уравнения функции у и графика зависимости функции у от фактора х и отправить преподавателю по электронной почте.

Смотрите также файлы