Файл: Отчет по лабораторной работе 2 одномерная статистическая модель.docx
Добавлен: 12.12.2023
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное автономное образовательное учреждение
Астраханской области высшего образования
«Астраханский государственный архитектурно-строительный университет»
Кафедра систем автоматизированного проектирования и моделирования
 Отчет
Отчетпо лабораторной работе №2
«ОДНОМЕРНАЯ СТАТИСТИЧЕСКАЯ МОДЕЛЬ»
Выполнил ст. группы ПГ-31-18
Кузнецов К.А.
(Ф.И.О.)
Преподаватель к.т.н., доцент
Евсина Е.М.
(Ф.И.О.)
| | дата | подпись |
| отчет | | |
Лабораторная работа №2
Одномерная статистическая модель.
Цель работы:
-
Расчёт статистических характеристик никеля.
Оборудование: 1. MatCAD
Ответы на контрольные вопросы
-
Реализация случайной величины
Одномерная статистическая модель применяется для изучения одного свойства. Пусть имеется система, состоящая из множества однородных геологических объектов. Выборочным методом возьмем из множества n объектов и у каждого из них измерим характеристику свойства х. Результаты измерений обозначим х1, х2, ..., хn и составим из них матрицу (1.1), в которой число строк равно n, а число столбцов k = 1.
В основе одномерной статистической модели лежат три гипотезы: а) измеренные значения х1, х2, ..., хn носят случайный характер; б) они не зависят друг от друга; в) значения образуют однородную совокупность. Измеренные значения принято называть реализациями случайной величины х.
-
Размах
Размах – это разность между максимальным хmax и минимальным хmin значениями свойства:
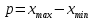
-
Медиана
Медиана – средний член упорядоченного ряда значений. Для нахождения медианы нужно расположить все значения в порядке возрастания или убывания и найти средний по порядку член ряда. В случае n – четного числа в середине ряда окажутся два значения, тогда медиана будет равна их полусумме.
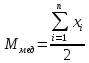
-
Мода
Мода – наиболее часто встречающееся значение случайной величины. Методику ее нахождения мы рассмотрим позднее.
-
Среднее значение
Среднее значение – это среднеарифметическое из всех измеренных значений:
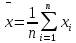
Существуют другие виды средних (среднее взвешенное, среднее геометрическое, среднее гармоническое и др.), которые вычисляются в особых случаях и здесь не рассматриваются.
-
Дисперсия
Дисперсия – это число, равное среднему квадрату отклонений значений случайной величины от ее среднего значения:
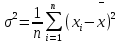
-
Среднеквадратичное отклонение
Среднеквадратичное отклонение – это число, равное квадратному корню из дисперсии:
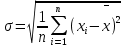
Среднеквадратичное отклонение имеет размерность, совпадающую с размерностью случайной величины и среднего значения. Например, если значения случайной величины измерены в метрах, то и среднеквадратичное отклонение также будет выражаться в метрах.
-
Коэффициент вариации
Коэффициент вариации – это отношение среднеквадратичного отклонения к среднему значению:
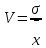
Коэффициент вариации выражается в долях единицы или (после умножения на 100) в процентах. Вычисление коэффициента вариации имеет смысл для положительных случайных величин
-
Ассиметрия
Асимметрия – степень асимметричности распределения значений случайной величины относительно среднего значения,
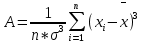
-
Экцесс
Эксцесс – степень остро- или плосковершинности распределения значений случайной величины относительно нормального закона распределения,
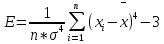
-
Математическое ожидание
Математическое ожидание случайной величины М(х) – это ее среднее значение в генеральной совокупности. Оно, за редким исключением, бывает неизвестно, и приходится пользоваться его приближенной оценкой (точечной оценкой) – выборочным средним значением x, определяемым по формуле. При увеличении числа наблюдений выборочное среднее стремится к пределу – к математическому ожиданию.
-
Дисперсия генеральной совокупности
Дисперсия генеральной совокупности D(х) – это число, равное среднему квадрату отклонений случайной величины от ее математического ожидания. Если математическое ожидание известно, то дисперсию находят по формуле.
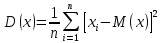
-
Моменты случайной величины, их связь со статическими характеристиками
Вычисление статистических характеристик можно производить непосредственно по формулам, но на практике характеристики обычно находят с помощью моментов.
Моментом случайной величины k-го порядка относительно постоянного параметра а называется выражение
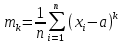
Порядок k может быть выражен любым целым числом, но интерес представляют первые четыре момента (порядка).
В зависимости от выбора параметра а различают начальные и центральные моменты. В первом случае а выбирается произвольно, что имеет смысл для ускорения вычислений. Часто полагают а = 0, и формула начальных моментов приобретает вид
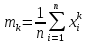
Во втором случае принимают a = x и получают центральные моменты
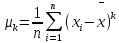
От начальных моментов можно перейти к центральным
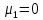
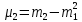
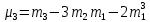
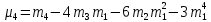
Зная моменты случайной величины, можно найти ее статистические характеристики по формулам
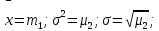
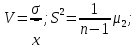
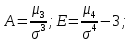
-
Группировка исходных данных
При большом числе исходных данных (n>50) расчет статистических характеристик с помощью таблиц становится громоздким, поэтому применяется компактный метод расчета с предварительной группировкой данных. Для этого весь диапазон исходных значений от х
min до хmax разбивается на равные интервалы (классы), границы которых удобно брать округленными, хотя это не имеет принципиального значения. С округленными границами удобнее работать.
Число классов зависит от числа исходных данных. Обычно принимается от 6 до 20 классов, но можно использовать и больше. Для определения числа классов рекомендуется эмпирическая формула Nкл = 16[0,4ln(n) – 1]. Далее подсчитывают число исходных значений, попавших в каждый класс, и результаты сводят в таблицу.
Некоторая трудность возникает в том случае, когда отдельные значения попадают на границу классов. Их можно относить в старший класс либо пытаться распределить примерно поровну между смежными классами.
Число значений в классе называется частотой. Если выразить частоту в относительных долях к общему числу значений, то получим частость. Ееможно выразить в процентах.
-
Построение гистограммы
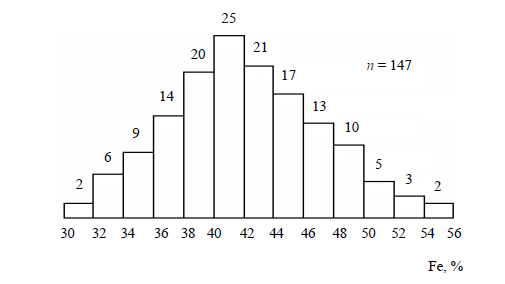
Данные табл.2.4 позволяют построить гистограмму значений случайной величины (рис.2.1). По оси абсцисс откладывают классы, а по оси ординат – частоту или частость в виде ступенек. Для удобства обозрения над ступеньками выписана частота, а рядом с гистограммой указано суммарное значение n.
Гистограмма дает наглядное представление о поведении случайной величины. На ней видны размах и частота значений. Полезную информацию несет и форма гистограммы; она может быть симметричной и асимметричной, с одним, двумя и более максимумами частот.
Н
аличие нескольких максимумов свидетельствует о неоднородности изучаемой совокупности и позволяет ставить вопрос о выделении однородных совокупностей. В некоторых случаях отдельные частоты резко преобладают, это чаще всего связано с дефектами измерений. Например, при химическом анализе часто встречаются округленные значения и гораздо реже – промежуточные между ними. Чтобы устранить влияние подобных погрешностей, следует увеличить размер классов и построить гистограмму снова.