_{Тема: Индуктивность. Энергия магнитного поля.}

Цель работы.

Ознакомление с основными параметрами катушек индуктивности и методами их измерений

Основные теоретические положения.

Движущиеся заряды порождают магнитное поле. Магнитное поле имеет направленный характер и характеризуется векторной величиной В, называемой электромагнитной индукцией. Было бы логично присвоить величине В, по аналогии с напряженностью электрического поля Е, название напряженность магнитного поля. Однако по историческим причинам это название носит вспомогательная величина Н, аналогичная вектору электрического смещения D. Связь между В и Н определяется следующей формулой:

B=₀H, (5.1)

где₀= 410^-7 Гн/м– магнитная проницаемость вакуума (воздуха); μ – относительная магнитная проницаемость вещества по отношению к вакууму.

Магнитное поле удается сконцентрировать внутри катушки, образованной множеством близко расположенных витков с током I. Если принять, что все составляющие индукции по сечению катушки S равны некоторому среднему значению В, что справедливо для катушек с сердечником, то отдельные значения B суммируются в полный поток электромагнитной индукции, или магнитный поток, определяемый как

 =BS = LI, (5.2)

где L – коэффициент пропорциональности между током и полным магнитным потоком катушки, называемый индуктивностью катушки. Индуктивность зависит от геометрии катушки, от магнитной проницаемости сердечника и от магнитных свойств окружающей среды. Так, для дросселей с замкнутыми тороидальными магнитопроводами индуктивность определяется формулой

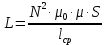, (5.3)

где N– количество витков; S – сечение магнитопровода; l_ср – средняя длина окружности, определяемая как полусумма длин окружностей внутреннего и внешнего контуров магнитопровода. В лабораторной работе используется сердечник с μ = 500, l_ср = 78 мм, S= 54 мм².

Единицей индуктивности является генри [Гн]. Одному генри соответствует индуктивность катушки без сердечника, которая развивает поток электромагнитной индукции в 1 Вб (вебер) в результате протекания тока 1 А.

---

В соответствии с законом Ленца изменение магнитного потока Ф, пронизывающего замкнутый контур, порождает в нем возникновение индуцированной ЭДС (Е):

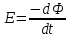. (5.4)

С учетом (5.2) из (5.4) получаем выражение для ЭДС катушки индуктивности при изменении протекающего через нее тока:

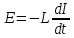. (5.5)

Из этого следует, что включение индуктивности последовательно с цепью нагрузки, питаемой от пульсирующего источника тока, снижает его пульсации за счет возникающей ЭДС самоиндукции. Если предположить, что ток в катушке изменяется от некоторого значения I до нуля, то работа, совершаемая этим током за время dt, будет определяться как dA = EIdt. Тогда, если индуктивность не зависит от тока, очевидно, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, катушка с индуктивностью L, через которую протекает ток I, запасает энергию W, равную

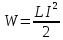. (5.6)

Катушка не может запасти энергию мгновенно. Ее нужно зарядить аналогично тому, как заряжают конденсатор. Если индуктивность подключается к источнику постоянного напряжения (U), то ее зарядка происходит по экспоненциальному закону:

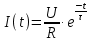, (5.7)

где R – полное активное сопротивление, ограничивающее ток индуктивности; τ = L/R – постоянная времени зарядки индуктивности.

Цепь, состоящую из катушки индуктивности и параллельно подключенного ей конденсатора, называют колебательным контуром. При работе индуктивности в составе колебательного контура, ее периодическая зарядка и разрядка происходят на резонансной частоте контура:

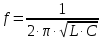, (5.8)

где С – емкость конденсатора, входящего в колебательный контур.

Поскольку в колебательном контуре происходит периодическое превращение энергии, запасенной в катушке индуктивности, в энергию заряженного конденсатора, то, в отсутствие потерь, справедливо:

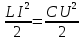. (5.9)

Поскольку работа контура сопровождается потерями энергии, используют понятие добротности колебательного контура, характеризующее скорость затухания колебаний.

---

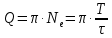, (5.10)

где N_e - число колебаний, в течение которых амплитуда снижается в «е» раз.



Рисунок5.1.Исследование колебательного контура

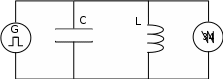
Рисунок 5.2. Схемаисследования колебательного контура
Обработка результатов эксперимента.

1. 
   Расчет теоретического и практического значений величины индуктивности исследуемой катушки.
   

Для теоретического значения используем формулу:

(5.11)

Для практического значения используем формулу:

(5.12)

Примеры расчета:

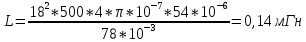(5.13)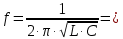



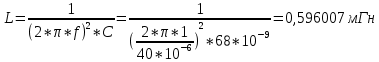(5.14)

Таб.1.Теоретическоеи практическое значений величины индуктивности исследуемой катушкив зависимости от кол-ва витков

Кол-во витков	8	10	12	14	16	18
Lтеор, мГн	0,028	0,043	0,06	0,09	0,11	0,14
Lпракт, мГн	0,149	0,21	0,292	0,43	0,537	0,596

2. 
   Расчет добротности колебательного контура по формуле
   

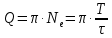(5.15)

Вычисление 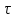по формуле: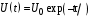

---

(5.16)


Расчеты:
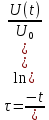(5.17)

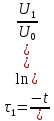(5.18)

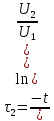(5.19)

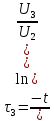(5.20)
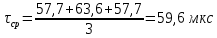(5.21)
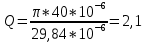(5.22)

3)Графики теоретической и экспериментальной зависимостей индуктивности катушки от количества витков


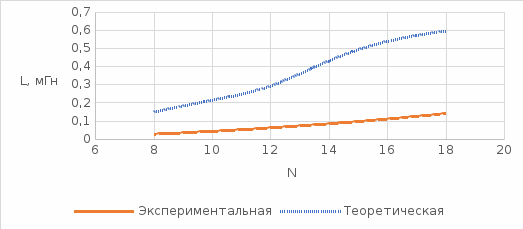
Рисунок 5.3. Зависимость индуктивности от количества витков

Выводы.

В данной лабораторной работы были исследованы основные параметры катушек индуктивности. При расчете индуктивности катушки было замечено, что практическое и теоретическое значение отличается. Данное отличие связано с погрешностью установки. Также были рассчитаны теоретические и экспериментальные зависимости индуктивности катушки от количества витков. На основании этих данных были построены графики, из которых видно, что при увеличении количества витков индуктивность возрастает. Была рассчитана добротность колебательного контура, которая оказалась равна 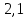, что соответствует теории.

---

Смотрите также файлы

• Недостаточность информации складывается на основе 4 групп.docx

• Безопасность на льду 78 класс Дата 141022 год.doc

• иялы дамыан жне ты идеялар табады 2 Кпіршелер трызу.docx

• Зрительные диктанты по федоренко и. Т.ppt

• Программа интегративного курса физического воспитания для обучающихся общеобразовательных учреждений на основе регби.doc