Федеральное государственное бюджетное образовательное учреждение высшего образования

«Санкт-Петербургский Горный университет»

Кафедра общей и технической физики

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №10

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ (МОДУЛЯ ЮНГА) ПО ДЕФОРМАЦИИ ИЗГИБА

Выполнил: студент гр. ГМ-20 _______________ / Гайфуллин М.М./

^{(подпись) (Ф.И.О.)}

Проверил: доцент _______________ /Егорова А.Ю./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

2020

Цель работы: определить модуль Юнга материала путём измерения прогиба стержня при механической нагрузке.

Теоретические основы лабораторной работы:

Деформация – это изменение объема кили формы тела без изменения его массы под действием внешний силы. Все возможные виды деформации могут быть сведены к двум основным деформациям: растяжению (или сжатию) и сдвигу, называемым элементарными деформациями. Деформации изгиба и кручения принадлежат к числу сложных деформаций. Их можно представить как сочетание элементарных деформаций, происходящих одновременно.

Мо́дуль Ю́нга (синонимы: модуль продольной упругости, модуль нормальной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации^[1]. Обозначается большой буквой Е.

Схема установки:



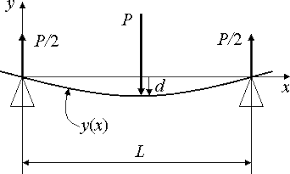
Общие сведения:

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гига Паскалях (10¹²Па)

Величину E для

---

стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Основные расчетные формулы:



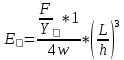
Где E- модуль Юнга, F-сила тяжести, Y- стрела прогиба стержня, h w-размеры поперечного сечения стержня , L- расстояние между опорами балки.

Погрешность прямых измерений:

Линейка( L)= 1 мм

Штангенциркуль( h, w)= 0,05 мм

Тензометр( Y)= 0,01 мм

Исходные данные:

L=40 мм

Материал стержня – сталь

g= 9,8 Н/кг



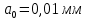
Таблицы:

	h		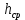	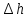w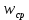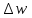
Ед. измерений	мм	мм	мм	мм	мм	мм
1	10,2	10,17	0,03	3,05	3,06	0,01
2	10,15	10,17	0,02	3,1	3,06	0,04
3	10,2	10,17	0,03	3,05	3,06	0,01
4	10,15	10,17	0,02	3,05	3,06	0,01
5	10,15	10,17	0,02	3,05	3,06	0,01

	Масса груза	F	n	Y	F/Y		E
Ед. измерений	кг	Н	делений	м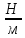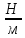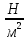
1	0,2	19,6	51	0,00051	3843	58	19103000
2	0,4	3,92	105	0,00105	3733	52	18556000
3	0,605	5,929	158	0,00158	3752	33	18651000
4	0,805	7,889	207	0,00207	3811	26	18944000
5	1,01	9,898	264	0,00264	3749	36	18636000
6	1,21	11,858	314	0,00314	3776	9	18770000
7	1,424	13,9552	369	0,00369	3782	3	18799000
8	1,624	15,9552	422	0,00422	3771	14	18745000
9	1,424	13,9552	370	0,037	3772	13	18750000
10	1,21	11,858	311	0,00311	3813	28	18954000
11	1,01	9,898	262	0,00262	3778	7	18780000
12	0,805	7,889	206	0,00206	3830	45	19059000
13	0,605	5,929	154	0,00154	3856	71	19168000
14	0,4	3,92	101	0,00101	3881	96	19292000
15	0,2	1,96	54	0,00054	3630	155	18044000

---

Пример вычисления:













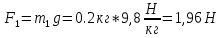
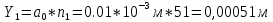
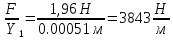
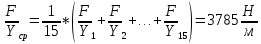
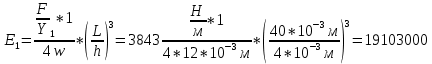
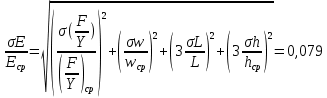
Вывод:

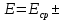
В этой работе я определил модуль Юнга, который равен: 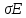= 18815400 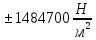путём измерения прогиба стержня при механической нагрузке. Сравнив с табличным значением (200* 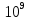Па) докажем, что материал стержня сталь

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м² или в Па.

---

Смотрите также файлы

• Реферат по дисциплине Психология Влияние речи родителей на развитие речи детей раннего возраста.docx

• Выполнение практических заданий по дисциплине история государства и права России 11.docx

• Проблема выбора. Спп с параллельным (неоднородным ) подчинением придаточных.docx

• Бюджет продаж пп.docx

• Анкета для учащихся Любите ли вы ЧупаЧупс Часто ли вы покупаете эти конфеты.ppt