Файл: Задача Найти матрицу, обратную матрице Ответ.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 12.12.2023

Просмотров: 24

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

Задача 1. Найти матрицу, обратную матрице 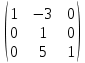Ответ:

Главный определитель
∆=1*(1*1 - 5*0) - 0*((-3)*1 - 5*0) + 0*((-3)*0 - 1*0) = 1
Определитель отличен от нуля, следовательно, матрица является невырожденной и для нее можно найти обратную матрицу A-1.
Обратная матрица будет иметь следующий вид:

A11
A21
A31

A12
A22
A32

A13
A23
A33










где Aij - алгебраические дополнения.
Транспонированная матрица.

AT=

1
0
0

-3
1
5

0
0
1










Найдем алгебраические дополнения матрицы AT.

A1,1 = (-1)1+1

1
5

0
1










∆1,1 = (1*1 - 0*5) = 1

A1,2 = (-1)1+2

-3
5

0
1










∆1,2 = -((-3)*1 - 0*5) = 3

A1,3 = (-1)1+3

-3
1

0
0










∆1,3 = ((-3)*0 - 0*1) = 0

A2,1 = (-1)2+1

0
0

0
1










∆2,1 = -(0*1 - 0*0) = 0

A2,2 = (-1)2+2

1
0

0
1










∆2,2 = (1*1 - 0*0) = 1

A2,3 = (-1)2+3

1
0

0
0










∆2,3 = -(1*0 - 0*0) = 0

A3,1 = (-1)3+1

0
0

1
5










∆3,1 = (0*5 - 1*0) = 0

A3,2 = (-1)3+2

1
0

-3
5










∆3,2 = -(1*5 - (-3)*0) = -5

A3,3 = (-1)3+3

1
0

-3
1










∆3,3 = (1*1 - (-3)*0) = 1
Обратная матрица.

1
3
0

0
1
0

0
-5
1











A-1=

1
3
0

0
1
0

0
-5
1










Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.

E=A*A-1=

1
-3
0

0
1
0

0
5
1









1
3
0

0
1
0

0
-5
1










E=A*A-1=

1*1+(-3)*0+0*0
1*3+(-3)*1+0*(-5)
1*0+(-3)*0+0*1

0*1+1*0+0*0
0*3+1*1+0*(-5)
0*0+1*0+0*1

0*1+5*0+1*0
0*3+5*1+1*(-5)
0*0+5*0+1*1





1
0
0

0
1
0

0
0
1











A*A-1=

1
0
0

0
1
0

0
0
1









Задача 2. Решить СЛАУ

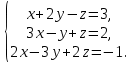
Ответ: {x+2y-z=3 (1)
{3x-y+z=2  (2)
{2x-3y+z=-1  (3)
прибавим (1) и (2),получим 4х+у=5
прибавим (1) и (3),получим 3х-у=2
прибавим
7х=7
х=1
4*1+у =5
у=5-4
у=1
подставим в (1)
1+2-z= 3
z=0
Ответ: (1 ;1;0)

Задача 3. Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен:

а) ровно 6-ти изделиям;

б) более чем 7-ми изделиям;

в) хотя бы одному изделию;

г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.

Решение.

Вероятность того, что изделию не будет присвоен знак «изделие высшего качества» равна   .

а)  ;

б) 

Смотрите также файлы