ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант I
1.Запишите уравнение прямой, параллельной прямой y = 4x – 5 и проходящей через точку (2; 5).
2. Функция задана формулой f (х) = х2 – 9.
а) Найдите f (6), f (–0,5).
б) Найдите значение аргумента, при котором значение функции равно –9; 7.
3. Вычислите координаты точки пересечения прямых 4х – у = 21 и 3х – 2у = 17.
4
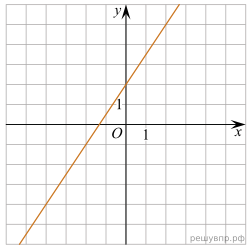. Найдите координаты точки пересечения прямой 
осью Ox.5. На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию.
6. Найдите область определения функции:
.Вариант II
1.Запишите уравнение прямой, параллельной прямой y = –3x + 2 проходящей через точку(3; 4).
2.Дана функция f (х) =
.а) Найдите значения f (–2); f (–1); f (3); f (6).
б) Постройте график функции y = f (х).
3. Вычислите координаты точки пересечения прямых 2х – 3у = 17 и х – 5у = 19.
4
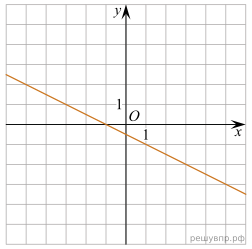.Найдите координаты точки пересечения прямой 
с осью Oy.На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию
6. Найдите область определения функции:
.