Файл: Контрольная работа 2 по предмету Теория электрических цепей Выполнил Группа Проверил 2007.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 79
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи.
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа №2
по предмету
Теория электрических цепей
Выполнил:
Группа:
Проверил:
2007
Вариант 01
КОНТРОЛЬНАЯ РАБОТА № 2
Задача 2.1
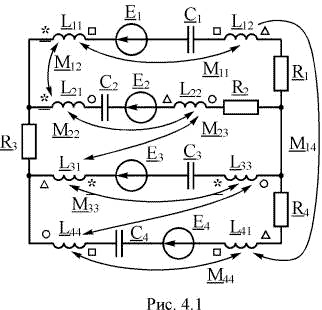
Задача посвящена анализу цепей, имеющих индуктивно связанные катушки.
На рис. 4.1 приведена общая схема цепи гармонического тока, состоящая из четырех ветвей. Согласно таблицы 4.1 схемы вариантов задачи содержат только по три ветви. В каждую их этих ветвей входят элементы R1C1, R2C2, R3C3, R4C4 соответственно. Комбинации из ЭДС Е, индуктивностей и взаимоиндуктивностей для десяти вариантов схем определяются таблицей 4.1.
Выполните следующее:
1. Составьте схему своего варианта, используя таблицы 4.1 и рис. 4.1. Одноименные зажимы катушек обозначены комбинациями:
– ; * – *; 
– ; 
– .2. Укажите направления токов ветвей и составьте уравнения электрического равновесия цепи по законам Кирхгофа в комплексной форме для действующих значений токов и ЭДС.
3. Запишите полное напряжение на каждой индуктивности схемы.
Таблица 4.1
| Номер схемы | Ветвь 1 | Ветвь 2 | Ветвь 3 | Ветвь 4 |
| 1 2 3 4 5 6 7 8 9 10 | E1L11L12M11 E1L12M14 L11M12L12M14 нет нет Е1L11M12 E1L11L12M11 L12M14 L12M14Е1 нет | E2L22M23 нет E2L21M12 E2L21L22M22 L22M23 E2L21M12 нет нет E2L21L22M22 E2L22M23 | L31M23 E3L33M34 нет L33M34 E3L31M23 нет Е3L33M34 E3L31L33M33 нет L31M23L33M34 | нет L41M14L44M34 E4L41M14 E4L44M34 E4L41L44M44 L41L44M44 L44M34 E4M14L41 L41M14 E4L44M34 |
Задача Т2.1
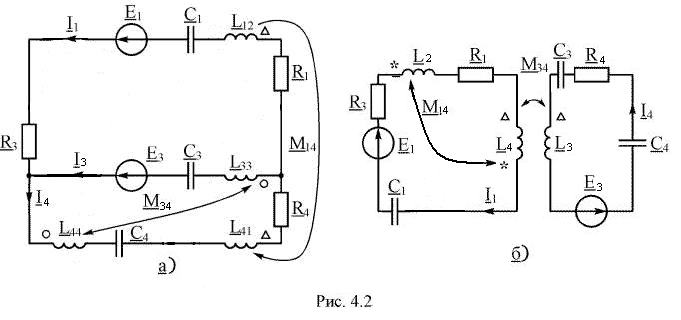
На рис. 4.2, а приведена схема цепи, которая составлена по рис.4.1 при условии, что: ветвь 1 имеет Е1 L11 М12; ветвь 2 имеет Е2 L21 М12; ветвь 3 имеет Е3 L31 L33 М33; ветви 4 нет. Указаны одноименные зажимы каждой пары катушек.
В схеме 4.2, а три неизвестных тока и два узла, поэтому составляется одно уравнение по закону Кирхгофа для токов и два уравнения по закону Кирхгофа для напряжений.
| 1 2 3 4 5 6 7 8 9 10 | E1L11L12M11 E1L12M14 L11M12L12M14 нет нет Е1L11M12 E1L11L12M11 L12M14 L12M14Е1 нет | E2L22M23 нет E2L21M12 E2L21L22M22 L22M23 E2L21M12 нет нет E2L21L22M22 E2L22M23 | L31M23 E3L33M34 нет L33M34 E3L31M23 нет Е3L33M34 E3L31L33M33 нет L31M23L33M34 | нет L41M14L44M34 E4L41M14 E4L44M34 E4L41L44M44 L41L44M44 L44M34 E4M14L41 L41M14 E4L44M34 |
При составлении уравнений по ЗНК для цепей, имеющих индуктивно связанные катушки необходимо знать следующее. Две катушки включены согласно, если токи, протекающие через них, входят в одноименные зажимы или включены встречно, если токи входят в разноименные зажимы. При согласном включении взаимная индуктивность М учитывается со знаком «плюс», при встречном включении – со знаком «минус». В качестве примера ниже представлена система из двух уравнений по ЗНК для схемы, показанной на рис. 4.2, б.
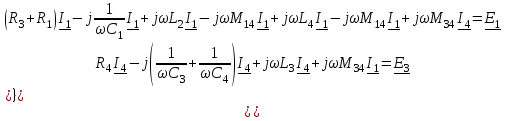
Полные напряжения на зажимах катушек будут:
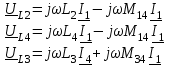
Задача 2.2
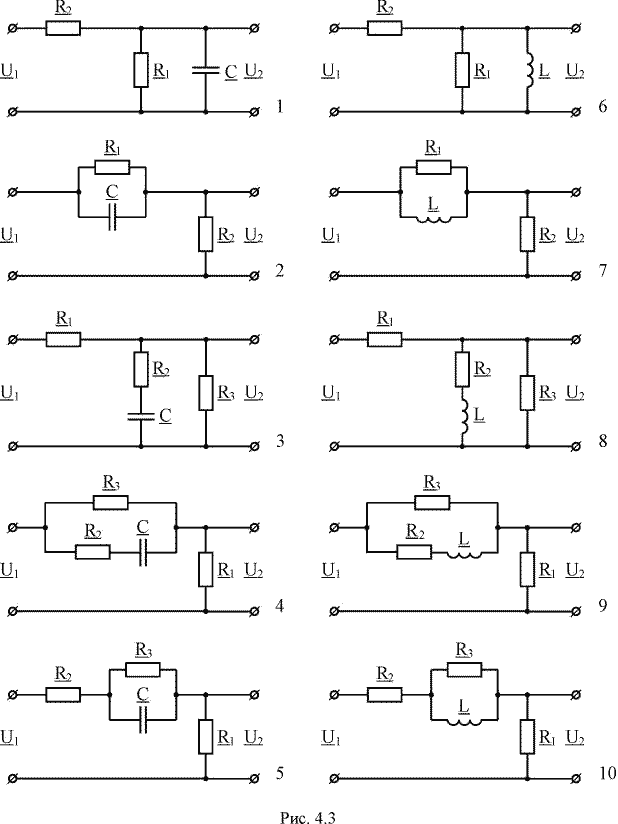
Задача посвящена расчету и построению графиков АЧХ и ФЧХ пассивных цепей. На рис. 4.3 приведены схемы цепей. Номер схемы и параметры элементов ее определяются по таблице 4.2. Во всех схемах R2 = 0,2R1. В схемах, где имеется сопротивление R3, его величина R3 = 3R1.
Выполните следующее:
1. Перерисуйте схему своего варианта и выпишите значения ее элементов.
2. Качественно постройте АЧХ цепи по напряжению.
3. Рассчитайте АЧХ и ФЧХ цепи, используя комплексную передаточную функцию по напряжению.
4. Постройте графики АЧХ и ФЧХ по результатам расчета.
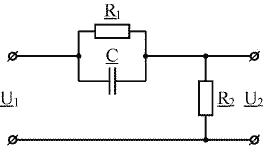
Задача Т2.2
Дана цепь, схема которой приведена на рис. 4.4, а. Значения элементов: R1 = 20 кОм, R2 = 0,2R1 = 4 кОм, С=10 нФ.
Решение
1. Качественное построение кривой АЧХ.
Обычно для качественного построения кривых АЧХ цепей, имеющих только один реактивный элемент, используется значение модуля комплексной передаточной функции по напряжению, рассчитанное на частотах w = 0 и w =
. Такой расчет удобно выполнить по эквивалентным схемам, составленным по исходной, но для частот w = 0 и w= (рис. 4.4, б и в соответственно). Для этих схем:
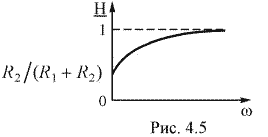
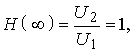
т. к. все напряжение U1 будет действовать на выходе схемы. По двум точкам строим кривую АЧХ (рис. 4.5).
2. Расчет АЧХ и ФЧХ цепи.
Расчет сводится к составлению таблицы зависимости модуля и аргумента комплексной передаточной функции от частоты. Наиболее простой вариант составления такой таблицы сводится к следующему. Записывают выражение для передаточной функции
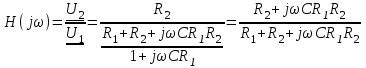(4.1)делают числовые подстановки
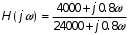
а затем, задавая различные значения частот, получают численные значения Н(jw), из которых выделять модуль и аргумент.
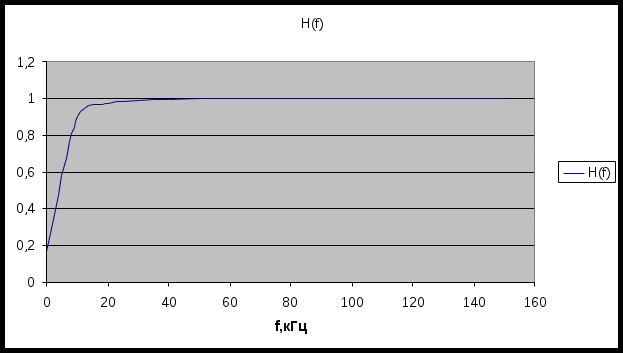
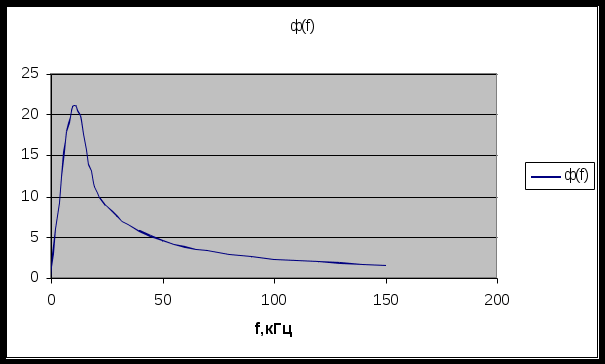
Таблица 4.3
| f, кГц | 0 | 10 | 50 | 100 | 250 |  |
| Н(f) | 0,167 | 0,905 | 0,996 | 0,999 | 1 | 1 |
| φ(f), град | 0 | 21 | 4,55 | 2,28 | 0,913 | 0 |
В таблицу 4.3 заносим значения: Н(f) = 0,19 и j(f) = 26°. При выборе расчетных значений частот обязательно присутствуют частоты f = 0 и f=
. Промежуточные значения частот в таблице 4.3 отражают только значительные различия Н(f) от значений Н(0) и Н( ). Так при f = 1 кГц – Н = 0,16, а при f = 500 кГц – Н = 0,98. Поэтому Н(f) на этих частотах в таблице нет.По данным таблицы 4.3 строятся кривые АЧХ и ФЧХ цепи (рис. 4.6).
Задача 2.3
Задача посвящена анализу работы параллельного колебательного контура с нагрузкой и без нагрузки.
На рис. 4.7 приведено две схемы работы параллельного контура с источником тока и с источником напряжения, имеющими большие внутренние сопротивления. Вид схемы и параметры элементов ее определяются по таблице 4.4. Во всех схемах сопротивление нагрузки Rн = 1,2 Rг.
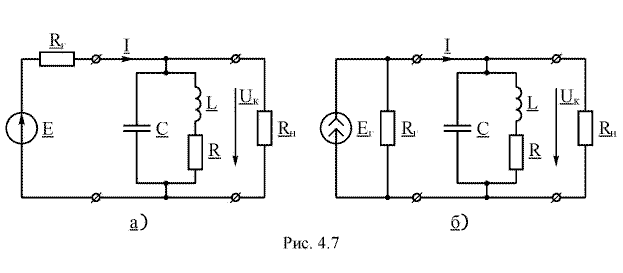
Выполните следующее
1. Перерисуйте схему своего варианта и выпишите значения ее элементов.
2. На резонансной частоте при Rн =
рассчитайте I0 – ток, подходящий к контуру, и токи в контуре IL0 и IC0.3. Рассчитайте напряжение на контуре Uк0 на резонансной частоте с учетом и без учета Rн.
4. Рассчитайте fн и fв – частоты на границе полосы пропускания контура с учетом и без учета Rн.
Таблица 4.4
| Варианты | Схема | Е, В | Iг, мА | Rг, кОм | L, мкГн | С, нФ | R, Ом |
| от 00 до 09 от10 до 19 от20 до 29 от30 до 39 от40 до 49 от50 до59 от 60 до 69 от70 до 79 от80 до 89 от 90 до 99 | а б а б а б а б а б | 5 – 8 – 10 – 12 – 14 – | – 5 – 7 – 9 – 11 – 13 | 10 6 8 7 9 8 8 9 9 10 | 125 117 116 111 129 105 122 120 120 114 | 3 1,5 3 1,5 2,5 1,5 2,3 1,2 2,2 1,2 | 5 6 3,5 5 5 4 4,5 6 4 5,5 |
5. Постройте кривые напряжения на контуре (резонансные кривые) в зависимости от частоты Uк(f) по трем точкам (на частотах