ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 108
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Геометрия 11 класс
Зачет № 4
по теме «Объёмы тел»
Вариант 1
1. Какое утверждение неверное?
1). Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
2). Равные тела имеют равные объёмы.
3). Если объёмы тел равны, то тела равны.
2. Какое утверждение верное?
1) Не могут быть равны объёмы четырёхугольной призмы и четырёхугольной пирамиды, имеющих равные высоты.
2) Две призмы с равными высотами равновелики, если их основаниями являются одноимённые многоугольники с равными сторонами.
3) Диагональные плоскости делят параллелепипед на равновеликие части.
3. Объем правильной шестиугольной призмы можно найти по формуле:
1)
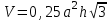 ; 2)
; 2) 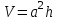 ; 3)
; 3) 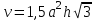 ,
, где
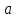 - сторона основания,
- сторона основания, 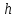 - высота призмы.
- высота призмы.4. S – площадь боковой поверхности цилиндра, R – радиус его основания. Тогда объем цилиндра равен:
1) RS; 2)
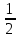 RS; 3) 2RS.
RS; 3) 2RS.5. Объем равностороннего конуса (длина образующей равна длине диаметра основания конуса) нельзя вычислить по формуле:
1)
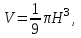 где
где 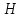 - высота конуса;
- высота конуса;2)
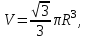 где
где 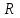 - радиус основания конуса;
- радиус основания конуса;3)
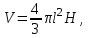 где
где 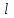 - образующая конуса.
- образующая конуса.6. Объем усеченного конуса, высота которого равна
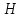 , вычисляется по формуле:
, вычисляется по формуле:1)
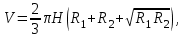 где
где 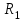 и
и 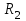
- радиусы оснований;
2)
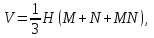 где
где 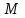 и
и 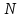 - площади оснований;
- площади оснований;3)
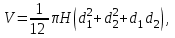 где
где 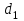 и
и 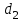 - диаметры оснований.
- диаметры оснований.7. Объем шара радиуса R можно найти по формуле:
1)
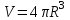 ; 2)
; 2) 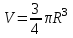 ; 3)
; 3) 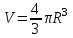 .
.8. Площадь поверхности шара диаметром d можно найти по формуле:
1)
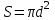 ; 2)
; 2) 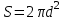 ; 3)
; 3) 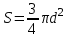 .
.9. Имеются шар и куб равного объема. У какого тела больше полная поверхность:
1) у шара; 2) у куба; 3) площади поверхностей тел равны.
Геометрия 11 класс
Зачет № 4
по теме «Объёмы тел»
Вариант 2
1. Какое утверждение верное:
1) Равные объемы могут иметь только равные тела.
2) Равновеликие тела – это тела, совмещаемые наложением.
3) Если первое тело содержит второе, то объем первого тела не меньше объема второго.
2. Какое утверждение верное:
1) Объемы двух правильных четырехугольных призм равны, если их диагональные сечения равновелики.
2) Два прямоугольных параллелепипеда с разными измерениями имеют разные объемы.
3) Два прямоугольных параллелепипеда разных объемов не могут иметь одинаковые измерения.
3. Объем правильной треугольной призмы можно найти по формуле:
1)
 ; 2)
; 2)  ; 3)
; 3)  ,
, где
 - сторона основания,
- сторона основания,  - высота призмы.
- высота призмы.4. Разверткой боковой поверхности цилиндра является квадрат со стороной
 см. Тогда объем цилиндра равен:
см. Тогда объем цилиндра равен:1)
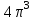 ; 2)
; 2) 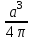 ; 3)
; 3) 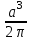 .
.5. Объем конуса можно найти по формуле:
1)
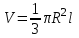 ; 2)
; 2) 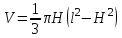 ; 3)
; 3) 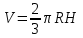 .
.6. Объем усеченного конуса, высота которого равна
 , вычисляется по формуле:
, вычисляется по формуле:1)
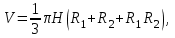 где
где  и
и  - радиусы оснований;
- радиусы оснований;2)
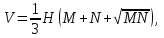 где
где  и
и  - площади оснований;
- площади оснований;3)
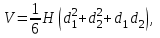 где
где  и
и  - диаметры оснований.
- диаметры оснований.7. Объем шара радиуса R можно найти по формуле:
1)
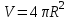 ; 2)
; 2)  ; 3)
; 3)  .
.8. Площадь сферы радиуса R можно найти по формуле:
1)
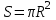 ; 2)
; 2) 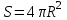 ; 3)
; 3) 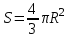 .
.9. Радиус шара уменьшили в 5 раз. Тогда площадь поверхности шара уменьшится:
1) в 2 раза; 2) в 10 раз; 3) в 25 раз.
Геометрия 11 класс
Зачет № 4
по теме «Объёмы тел»
Вариант 3
1. Площадь полной поверхности куба равна 6 см2. Найдите его объем.
2. Диагональ правильной четырехугольной призмы равна 3, 5 см, а диагональ боковой грани – 2,5 см. Найдите объем призмы.
3. Площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее, равна 36 см2. Радиус основания цилиндра равен 5 см. Найдите его объем.
4. Диагональ квадрата, лежащего в основании правильной пирамиды, равна 8 дм, а ее высота – 12 дм. Найдите объем пирамиды.
5. Радиус основания конуса равен 20 см, расстояние от центра основания до образующей равно 12 см. найдите объем конуса.
6. В наклонной призме основание – прямоугольный треугольник. Гипотенуза которого равна 4 см, один острый угол 30о. боковое ребро равно 5 см и составляет с плоскостью основания угол 60о. Найдите объем призмы.
7. Сколько шариков диаметром 2 см можно отлить из металлического куба с ребром 4 см?
8. Площадь поверхности полушара равна 18
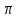 см2. Найдите объем шара.
см2. Найдите объем шара.Геометрия 11 класс
Зачет № 4
по теме «Объёмы тел»
Вариант 4
1. Измерения прямоугольного параллелепипеда относятся как 2 : 3 : 4. Диагональ параллелепипеда равна
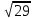 см. Найдите объем параллелепипеда.
см. Найдите объем параллелепипеда.2. Основанием прямой призмы служит прямоугольный треугольник с катетами 6 см и 8 см. высота призмы равна радиусу вписанной в основание окружности. Найдите объем призмы.
3. Площадь сечения, проведенного параллельно оси цилиндра на расстоянии 3 см от нее, равна 64 см2. Радиус основания цилиндра равен 5 см. Найдите его объем.
4. Основанием пирамиды является прямоугольный треугольник с катетами 6 см и 8 см. Каждое боковое ребро равно 13 см. Найдите объем пирамиды.
5. высота конуса равна 20 см, расстояние от центра основания до образующей равно 12 см. Найдите объем конуса.
6. в наклонной треугольной призме стороны основания равны 5 см, 6 см и 9 см. Боковое ребро равно 10 см и составляет с плоскостью основания угол 45о. Найдите объем призмы.
7. сколько кубиков с ребром 2 см можно отлить из металлического шара диаметром 4 см?
8. Объем шара равен
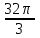 см3. Найдите площадь поверхности полушара.
см3. Найдите площадь поверхности полушара.Геометрия 11 класс
Ответы к зачету № 4 по теме «Объёмы тел»
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1 | 3 | 3 | 1 | 24 |
| 2 | 3 | 3 | 3 | 48 |
| 3 | 3 | 1 | 150 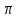 | 200 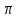 |
| 4 | 2 | 2 | 128 | 96 |
| 5 | 3 | 2 | 2000 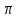 | 1500 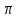 |
| 6 | 3 | 2 | 15 | 100 |
| 7 | 3 | 2 | 16 | 4 |
| 8 | 1 | 2 | 18 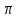 | 8 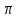 |
| 9 | 2 | 3 | | |