ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 190
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

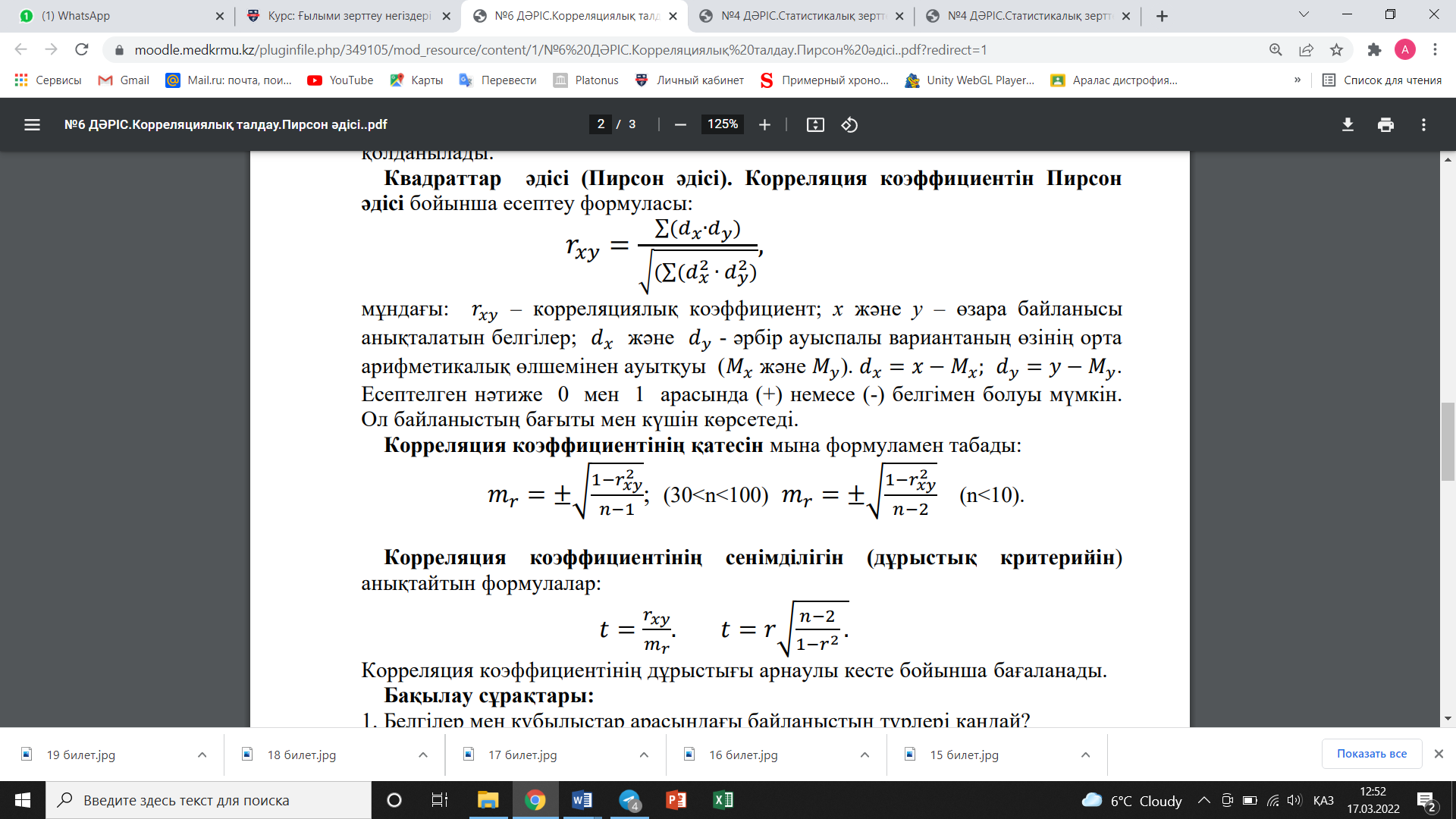
20 – билет . Пирсонның Хи-квадрат келісім критерийі.
Пирсонның Хи-квадрат келісім критерийі таралудың заңы жөніндегі жай жорамалды тексеру үшін ең жиі қолданылатын критерий. Тексеру үшін нөлдік жорамалды ұйғарады Н0: “эмпирикалық таралу мен теориялық таралудың арасында ешқандай айырмашылық жоқ”. Критерийді қолданудың негізгі идеясы теориялық жиіліктер мен эмпирикалық жиіліктерді салыстыру болып табылады. Егер эмпирикалық жиіліктер (ni) теориялық жиіліктерден (npi) қатты ерекшеленетін болса, онда тексерілетін жорамалды жоққа шығару керек; керісінше жағдайда қабылдау қажет.
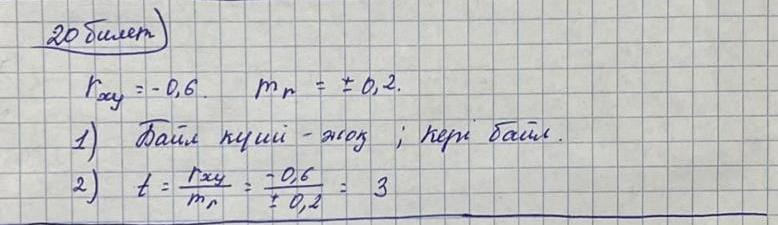
21 – билет . Статистикалық жиынтықтағы белгінің қалыпты таралуы. Гаусс қисығы.
Қалыпты (Гаусстық) таралу
Таралуы олардың басқа түрлеріне қарағанда жиірек кездесетін және статистикадағы ең маңызды таралулардың бірі - қалыпты таралу.
Қалыпты таралу түрінде варианталар вариациялық қатардың ортасына қарасты симметриялы түрде орналасады және олардың саны орталықтан алыстаған сайын біртіндеп кеміп отырады, сонымен бірге бақылаудың ең көп саны қатардың ортасына жинақталады.
Кездейсоқ шамалардың мұндай таралу түрі медициналық-биологиялық көрсеткіштерде жиірек кездесетін болғандықтан, оны «қалыпты» деп атаған.
Гаусс қисығы - Қалыпты таралудың графигі орта мәнге қатысты симметриялы, қоңырау тәрізді болады және қалыпты таралу қисығы немесе Гаусс қисығы деп аталады.
Қалыпты таралудың негізгі сипаттамалары:
-
толығымен екі параметрмен анықталады: орта мән және
-
дисперсия;
-
қоңырау тәріздес(унимодальды);
-
орта мәнге қатысты симметриялы;
-
егер орта мән ұлғайса оңға қарай, орта мән азайса солға қарай
-
жылжиды(дисперсия түрақты жағдайда);
-
қисықтың түрі бас жиынтықтың стандарттық ауытқуымен
-
анықталады;
-
стандарттық ауытқуы аз таралуға жіңішке, жоғары созылған
-
қисықтар, ал стандарттық ауыткуы үлкен таралуға жазыңқы қисықтар
-
сәйкес келеді.
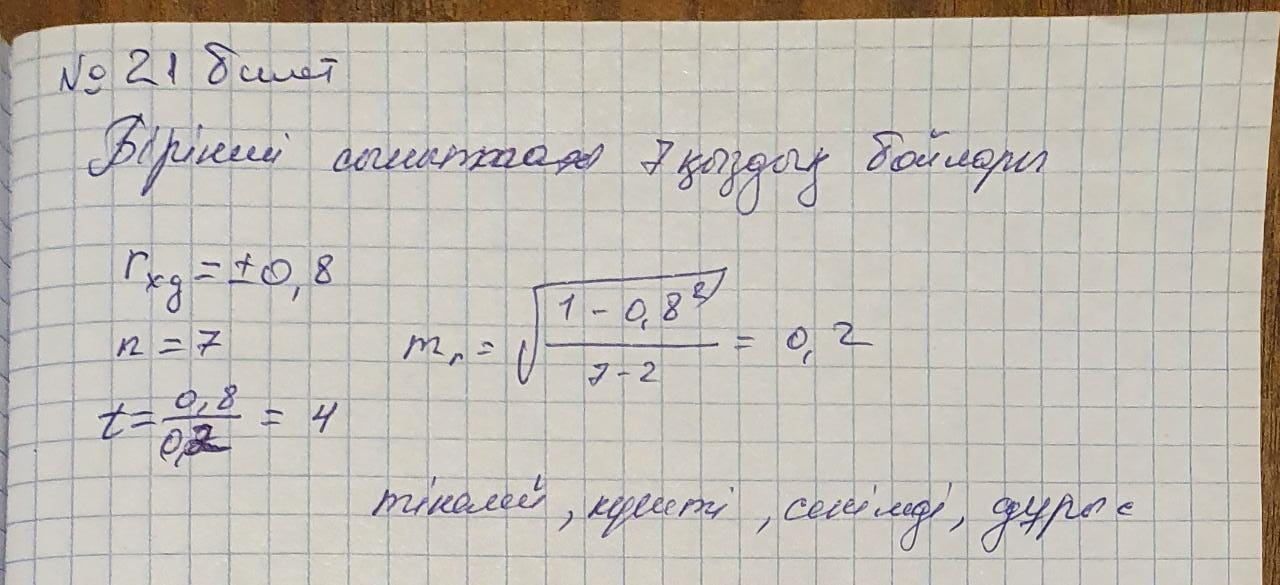
22 – билет. Корреляциялық талдау. Пирсон әдісі.
Корреляциялық байланысты бейнелеу тәсілдері: кестелік, графикалық (шашырау диаграммасы), корреляция коэффициенті. Егер нәтижелік белгінің бір факторға байланысын қарастырса, оны парлық корреляция дейді де, ал екі немесе бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді. Корреляциялық талдау жасау корреляциялық кесте мәліметтеріне сүйенеді. Мұндай кестелер екі түрде болады. Бірінде ол кесте мәліметтерді санау арқылы жасалса, екіншісінде қарапайым корреляциялық кесте, корреляциялық тор немесе корреляциялық матрица күйінде болады. Ал, графикалық тәсілдің мақсаты – корреляциялық өріс құру. Корреляциялық байланыс бағыты бойынша: тікелей, кері болып бөлінеді.
Квадраттар әдісі (Пирсон әдісі). Корреляция коэффициентін Пирсон әдісі бойынша есептеу формуласы: ???????????? = ∑(????????∙????????)/√(∑(???????? 2 ∙ ???????? 2 ) ,
мұндағы: ???????????? – корреляциялық коэффициент; x және y – өзара байланысы анықталатын белгілер;
???????? және ???????? - әрбір ауыспалы вариантаның өзінің орта арифметикалық өлшемінен ауытқуы (???????? және ????????). ???????? = ???? − ????????; ???????? = ???? − ????????. Есептелген нәтиже 0 мен 1 арасында (+) немесе (-) белгімен болуы мүмкін. Ол байланыстың бағыты мен күшін көрсетеді.
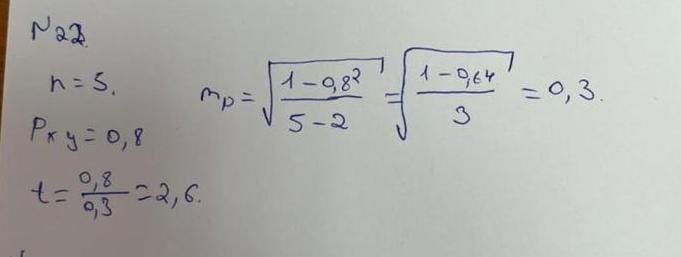
23 – билет. Корреляциялық талдау. Спирмен әдісі.
Корреляциялық байланысты бейнелеу тәсілдері: кестелік, графикалық (шашырау диаграммасы), корреляция коэффициенті. Егер нәтижелік белгінің бір факторға байланысын қарастырса, оны парлық корреляция дейді де, ал екі немесе бірнеше факторға байланысын қарастырса, оны көп өлшемді корреляция дейді. Корреляциялық талдау жасау корреляциялық кесте мәліметтеріне сүйенеді. Мұндай кестелер екі түрде болады. Бірінде ол кесте мәліметтерді санау арқылы жасалса, екіншісінде қарапайым корреляциялық кесте, корреляциялық тор немесе корреляциялық матрица күйінде болады. Ал, графикалық тәсілдің мақсаты – корреляциялық өріс құру. Корреляциялық байланыс бағыты бойынша: тікелей, кері болып бөлінеді.
Рангілік әдісті қолдану жөніндегі нұсқаулар: 1) егер байланыс күшінің деңгейін нақты түрде білу қажет болмаса, ондай мәліметтерді болжамдап алуға болады (яғни, дәл сандық өлшеммен анықталмайтын құбылыстар арасындағы байланысты ашу немесе оны бағалау қажет болғанда). 2) егер белгілер (n≤ 30) сандық және сапалық (атрибутивтік) белгілер болса; 3) белгілердің үлестірім қатары ашық варианталар болса (мысалы, жұмыс өтілі 1 жылға дейін).
Рангілік әдіс. Корреляция коэффициентін Спирмен әдісі бойынша есептеу формуласы: ???????????? = 1 – 6/∑ ???? 2 ????∙(????2−1) ,
мұндағы: ???????????? – рангілі корреляция коэффициенті; d – рангтардың айырмашылығының ауытқуы: d=x-y; n–бақылау саны. Есептелген нәтиже 0 мен 1 арасында (+) немесе (-) белгімен болуы мүмкін. Ол байланыстың бағыты мен күшін көрсетеді. Корреляция коэффициенті +1,0 немесе - 1,0 болса, оны толық (функционалдық) байланыс дейді.

24 – билет. Регрессиялық талдау, регрессия коэффициенті, қолданылуы.
Екі айнымалы шаманың бір-бірімен байланысының бағыты мен күші корреляциялық көрсеткіш арқылы анықталады. Ал, бір белгі мөлшерінің екінші белгінің мөлшері өзгергенде сан жағынан қаншалықты өзгеретіні регрессия әдісі арқылы анықталады. Регрессия – бір-бірімен байланысты белгілердің бірінің шамасы белгілі болса, екіншісінің орта шамасын табуға мүмкіншілік беретін әдіс. Мысалы, 1 сынып оқушыларының бойы 1 см-ге ұзарса салмағы қаншалықты өзгеретінін регрессиялық талдау арқылы анықтайды. Көбінесе, регрессиялық әдіс физикалық дамудың нормативті шкалалары мен стандарттарын жасау үшін қолданылады. Осы мақсатта регрессия коэффициенті және басқа да параметрлер қолданылады.
Регрессия коэффициенті – абсолюттік шама, ол бір белгінің мөлшері бірлік санға өзгергенде екінші белгінің өлшемі қаншалықты өзгеретінін көрсетеді. Регрессия коэффициентін есептеу формуласы:
????????⁄???? = ???????????? ∙ ???????? ???????? .
Мұндағы, ????????⁄???? - регрессия коэффициенті, ???????????? - корреляция коэффициенті, ???????? және ???????? - X және Y қатарларының орта квадраттық ауытқулары.

25 – билет. Сызықты регрессиялық талдау, теңдеуі, параметрлері.
Регрессия коэффициенті арқылы бір белгінің (мысалы, салмақтың) мөлшерін арнайы өлшеу жүргізбей-ақ, екінші белгінің (мысалы, бойдың) орта шамасы бойынша табуға болады. Ол үшін сызықты регрессия теңдеуін қолданады:
???? = ???????? + ????????⁄???? (???? − ???????? ).
Мұндағы, ???? - ізделіп отырған белгінің (салмақтың)шамасы; ???? - бірінші белгінің (бойдың) шамасы; ????????⁄???? – салмақты бойға салыстырғандағы регрессия коэффициенті; ???????? (белгілі жасқа тән салмақтың орта шамасы), ???????? (бойдың орта шамасы) – ???? және ???? белгілерінің белгілі орта шамалары. Мысал: 9 жасар қыздардың орта есеппен салмағы ????????= 30,3 кг., бойының ұзындығы орта есеппен ????????= 135,5 см. Егер 9 жасар қыздардың орта есеппен бойының ұзындығы: ???? = 132 см болса, онда салмағының орта шамасы қандай болатынын табуға болады: ???? = ???????? + ????????⁄???? (???? − ???????? ) = 30,3 + 0,43 (132 – 135,5) = 28,8 кг.
Сонымен, қорытынды: орта есеппен 9 жасар қыздардың бойының ұзындығы 132 см болса, бұған сәйкес салмақтың мөлшері орта шамамен 28,8 кг болады. Бұл теңдеу екі белгінің арасында түзу сызықты байланыс болғанда қолданылады.
Регрессия теңдеуінің графигі – регрессия сызығы. Жеке адамдардың белгілерінің мөлшері әртүрлі. Мысалы, бойларының ұзындығы бірдей болғанымен табылған салмаққа тән өзгерушіліктің шамасын анықтау үшін регрессия коэффициентінің ауытқуы қолданылады. Регрессияның орта квадраттық ауытқуы нәтижелік белгінің (y) өлшемінің әртүрлі болуына сипаттама береді. Ол мына формуламен есептеледі: ????????????⁄???? = ???????? ∙ √1 − ???????????? 2 . Мұндағы, ????????????⁄???? - сигма (орта квадраттық ауытқу); ???????? - y-зерттелінетін белгінің (мысалы, салмақтың) орта квадраттық ауытқуы; ???????????? - x және y белгілері арасындағы корреляция коэффициенті. Неғұрлым ????????????⁄???? - тың мөлшері аз болса, соғұрлым әр адамның зерттелген белгісінің орта шамасынан айырмашылығы аз болады. ????????= ± 4,2; ????????????= +0,6; ????????????⁄???? = ???????? ∙ √1 − ???????????? 2 = 4,2 ∙ √1 − 0,6 2 = +3,36 кг. Регрессия теңдеуін және регрессия ауытқуын пайдаланып регрессия коэффициенті арқылы регрессия шкаласын құрады. Бұл шкала бойынша балалардың және жас өспірімдердің дене дамуын зерттегенде бойдың, салмақтың, кеуде көлемінің мөлшерінің жасына сәйкестігін бағалайды. Бұнда, егер бала денесінің салмағы нақты бір бой ұзындығы бойынша регрессияның 1 сигмасы шегінде: ???? ± 1????????????⁄???? болса, онда физикалық даму салмақ бойынша гармониялы деп саналады. Ал, егер ???? ± 2????????????⁄???? болса, онда физикалық даму дисгармониялы деп; ???? ± 3????????????⁄???? болса, қатты дисгармониялы деп есептеледі (яғни, салмағы өте артық немесе өте кем). Бұл регрессиялық әдіс дәрігерлердің күнделікті жұмысында да қолданылады. Регрессия шкаласы бойынша қан қысымының ең жоғарғы деңгейі белгілі болса, оған сәйкес ең төменгі деңгейін табуға болады.
