ЛАБОРАТОРНАЯ РАБОТА №102

ИЗУЧЕНИЕ ПРУЖИННОГО МАЯТНИКА

Учебная цель занятия:

Колебательные движения исключительно широко распространены в природе и технике. Вибрация натянутой струны, движение поршня дизеля и ножей косилки, суточные и годичные изменения температуры воздуха, морские приливы и отливы, волнение водной поверхности, тепловое движение ионов кристаллической решётки твёрдого тела, переменный ток и его электромагнитное поле, движение электронов в атоме и т.д.- всё это в конечном счёте колебательные процессы. В данной работе изучаются собственные колебания пружинного маятника и определяются основные характеристики затухающих колебаний. Умения и навыки работы с простыми системами помогут понять физическую суть многих колебательных процессов разной природы.

Содержание лабораторной работы.

Необходимо экспериментально определить коэффициент упругости, зависимость периода собственных колебаний пружинного маятника от коэффициента упругости, коэффициент затухания колебаний.

Базовый материал.

Для успешного выполнения и сдачи работы необходимо знать основные кинематические и динамические характеристики колебательного движения, а также характеристики затухающих колебаний. Кроме того, необходимо уметь возводить числа в дробную степень, обладать навыками логарифмирования, решать дифференциальные уравнения второго порядка.

Подготовка к занятию:

Повторить, а по необходимости, изучить вопросы базового материала. (Например, 1. Р.И. Грабовский Курс физики.- М.: Высшая школа, 1980, стр.88-100, 2. Б.М.Яворский, А.А. Детлаф Справочник по физике.- М.: Наука, 1980, стр.299-323, 3. лекционный материал).

Входной контроль (самопроверка)

Подготовка к лабораторной работе контролируется по подготовленному бланку лабораторной работы, согласно общим требованиям и ответам на вопросы:

---

1. 
   Как определяется удлинение пружины?
   
2. 
   Чем характеризуется положение равновесия системы?
   
3. 
   Изменится ли положение равновесия при изменении массы груза, жесткости пружины?
   
4. 
   Почему начальная амплитуда колебаний маятника не должна быть слишком большой?
   
5. 
   Какой должна быть начальная масса груза в первом задании?
   
6. 
   Какое число колебаний п нужно брать при определении амплитуды затухающих колебаний?
   

Приборы, материалы, оборудование:

Пружинный маятник, грузы, штатив с вертикальной шкалой, секундомер.

Теоретическое введение и исходные данные:

Колебательные движения, или колебания, чрезвычайно широко распространены в природе и технике. Различают колебания механические, электромагнитные, электромеханические и другие, в зависимости от физической природы.

Механическим колебательным движением называется процесс, при котором тело или система тел, будучи выведена из положения равновесия, проходит это положение по инерции, каждый раз вновь отклоняясь от него.

Колебания называются периодическими, если система приходит в положение равновесия через равные промежутки времени.

Гармоническими колебаниями (или простыми) называются такие периодические колебания, в которых смещение тела или системы от положения равновесия совершаются по закону синуса (или косинуса).

Целью лабораторной работы является изучение законов колебательного движения на примере колебательной системы – пружинном маятнике.

При рассмотрении колебаний пружинного маятника вам необходимо:

а) пренебречь сопротивлением среды, считая груз маятника материальной точкой;

б) пренебречь массой пружины;

в) учесть, что на маятник, находящийся в положении равновесия, действует две силы: сила тяжести и сила упругости пружины, равные друг другу, но направленные противоположно;

г) при перемещениях маятника вниз от положения равновесия возникает дополнительная сила упругости, направленная к положению равновесия. То же самое будет и при отклонения маятника вверх, но природа силы будет иная. Это – равнодействующая силы тяжести и не полностью компенсирующей ее силы упругости пружины. Но по величине эта равнодействующая пропорционально величине смещения х от положения равновесия маятника. Таким образом, возвращающая сила, действующая на отклоненный маятник, - это сила квазиупругая, равная

---

где к – это коэффициент пропорциональности, именуемый жесткостью пружины.

Тогда II закон Ньютона может быть записан в виде:

где m – масса маятника.

Преобразовав это уравнение к виду



и представив , получим динамическое уравнение свободных незатухающих гармоничных колебаний:

.

Подстановкой легко убедится в том, что решение дифференциального уравнения (1) будет функция

.

Формула (2) выражает смещение х пружинного маятника в любой момент времени.

Выражение (2) является кинематическим уравнением гармонического колебания в общем виде.

Здесь А - амплитуда, т.е. максимальное отклонение от положения равновесия;

- фаза, т.е. аргумент функции, описывающий гармоническое колебание; - начальная фаза колебания.

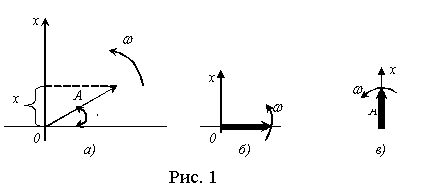
Не трудно убедится в том, что незатухающее колебательное движение подобно движению проекции но ось х вектора А, вращающегося относительно точки 0 равномерно, с угловой скоростью ₀. На этом основан способ изображения колебания с помощью векторной диаграммы – один из распространенных, особенно в электронике, способов. Если положить, что на рис. 1а указано начальное угловое положение вектора А, то рис. 1а является векторной диаграммой колебания, описанного управлением (2).

Обычно за начало отсчёта (t=0) принимают момент времени, когда система находится в положении равновесия или в положении максимального отклонения. В первом случае колебание может быть задано векторной диаграммой, изображённой на рис. 1б, или уравнением

. (3)

Во втором случае –векторной диаграммой, изображённой на рис.1в, или уравнением

---

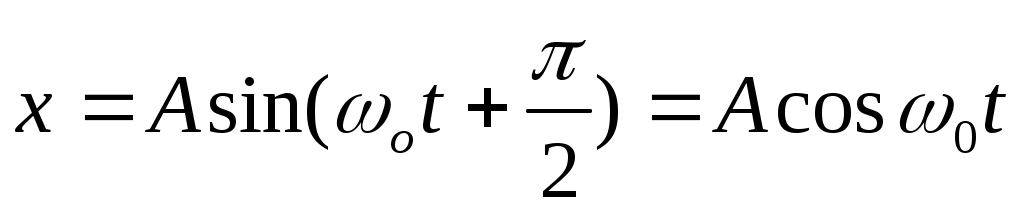(4)

Очевидно, что один оборот вектора А на векторной диаграмме соответствует

одному полному колебанию проекции конца этого вектора.

Из закономерностей вращательного движения известно, что

(5)



Где применительно к колебательному движению

Т-период колебания, т.е. время одного полного колебания;

-частота колебаний, т.е. количество колебаний за единицу времени;

-круговая (или циклическая) частота незатухающих гармонических колебаний, т.е. количество колебаний за единиц времени.

Величина в уравнениях (1-4) может быть при необходимости заменена её выражением (5)

Из (5) следует: .

Учитывая, что , получим: . (6)

из (6) видно, что период колебаний пружинного маятника пропорционален квадратному корню из его массы и обратно пропорционален квадратному корню из жесткости. В пределах деформаций пружины х, при которых выполняется закон Гука, период колебаний не зависит от амплитуды колебаний.

Выясним физический смысл коэффициента упругости (жесткости) к.

,

где F_д – внешняя (деформирующая) сила.

В соответствии с III законом Ньютона . Следовательно, коэффициент упругости к численно равен внешней силе, вызывающий деформацию пружины, равную единице длины.

Мы рассматривали свободные не затухающие колебания, пренебрегая сопротивлением среды и массой пружины. Частоту таких колебаний и соответствующую ей круговую частоту 

---

₀ называют собственной. Реальные свободные колебания – колебания затухающие. Динамическое уравнение таких колебаний:

. (8)

Решением этого дифференциального уравнения является кинематическое уравнение затухающих колебаний:

, (9)

где х – смещение колеблющейся точки;

А_о – начальная амплитуда;

е - основание натуральных логарифмов;

- коэффициент затухания;

- начальная фаза;

t – время (положительность) колебаний;

- круговая (циклическая) частота свободных затухающих колебаний.

Величины круговых частот свободных затухающих и не затухающих колебаний в общем не создают. Известно соотношение между ними:

.

При , что справедливо для случая колебаний пружинного маятника в воздухе:

.

Амплитуда при затухающих свободных колебаниях уменьшается с течением времени по закону: .

Скорость затухания колебательного движения принято характеризовать декрементом затухания . Декрементом затухания называют отношение двух амплитуд, разделенных интервалом времени, равным периоду колебания (рис. 2):

.

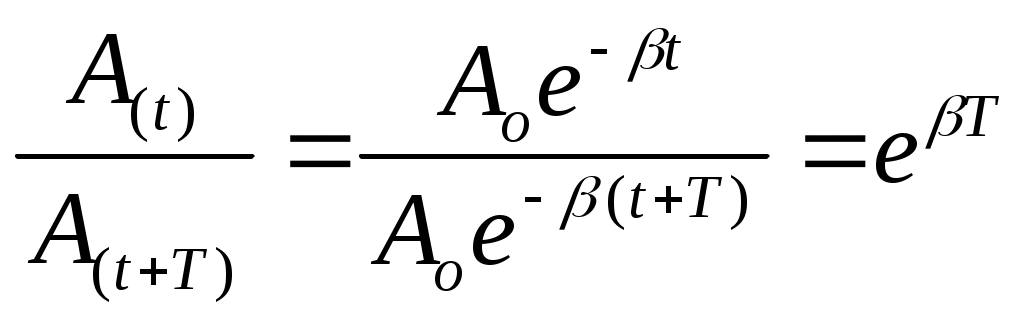Натуральный логарифм такого отношения назвали логарифмическим декрементом затухания :

(1)

Отсюда видно, что , т.е. коэффициент затухания равен отношению логарифмического декремента к периоду колебания.

---

Смотрите также файлы

• Программа среднего профессионального образования Право и организация социального обеспечения Дисциплина Статистика.docx

• Упражнение Доброе утро!.docx

• На окраине Каира столицы современного Египта самая высокая пирамида Хеопса Центральная Америка к северу от Мехико город Теотиукан.ppt

• Рабочая программа внеурочной деятельности Занимательная информатика.doc

• Задание. Прочитайте текст. Определите тему текста. 1 балл.docx