ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 341
Скачиваний: 22
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дисциплина: «Теоретические основы электротехники 3»
ПРОМЕЖУТОЧНЫЙ ТЕСТ 1
Между электродами сферического конденсатора находится диэлектрик, удельная проводимость которого меняется в функции расстояния r от центра сферы по закону
, a = 10–4 См. Радиусы внутренней и внешней обкладок соответственно R1 = 1 см и R1 = e см. Ток утечки через несовершенную изоляцию 
А. Определить напряжение между электродами.Ответ:
Сферический конденсатор с двухслойным диэлектриком имеет радиус внутренней обкладки, сферической поверхности, разделяющей диэлектрики, и радиус внешней обкладки соответственно r1 = 2 см, r2 = 6 см, r3 = 10 см, удельные проводимости слоёв
См/м, 
См/м. Определить проводимость утечки через изоляцию конденсатора (можно воспользоваться аналогией с электростатическим полем). Ответ записать в нСм.Ответ:
Два провода, имеющие одинаковые площади поперечного сечения S, но различные удельные сопротивления ρ1 = 3⋅10–7 Ом·м и ρ2 = 10⋅10–7 Ом·м, соединены встык. По проводникам течёт ток I = 27⋅π А. Найти величину заряда q, который возникнет в сечении стыка, если нормальная составляющая напряжённости электрического поля на поверхности раздела проводников удовлетворяет условию
. Ответ записать в (10–18 Кл).Ответ:
Заземлитель выполнен в виде полусферы радиусом R = 0,2 м, погружённой в грунт вблизи поверхности земли (большой круг полусферы лежит в плоскости земли). Через заземлитель протекает ток I = 1000⋅π А. Определить плотность тока δ в земле вблизи поверхности заземлителя.
Ответ:
Цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутренней обкладки, цилиндрической поверхности, разделяющей диэлектрики, и радиус внешней обкладки соответственно r1 = 2 см, r2 = 4 см, r3 = 8 см, удельные проводимости слоёв γ1 = 2⋅10–8 См/м, γ2 = 8⋅10–8 См/м. Длина конденсатора
см. Определить проводимость утечки через изоляцию конденсатора (можно воспользоваться аналогией с электростатическим полем). Ответ записать в нСм.Ответ:
Заземлитель в виде полусферы радиусом R погружён в глинистый грунт вблизи поверхности земли (большой круг полусферы лежит в плоскости земли). Удельная проводимость грунта
См/м. Сопротивление заземления составляет R0 = 20 Ом. Определить радиус заземлителя R. Ответ выразить в см.Ответ:
Плоский конденсатор с двухслойным диэлектриком имеет площадь обкладок S = 36 см2, толщину слоёв d1 = 2 см, d2 = 1 см, удельные проводимости слоёв γ2 = 2⋅10–9 См/м, γ2 = 8⋅10–9 См/м. Определить проводимость утечки через изоляцию конденсатора. Ответ записать в пСм.
Ответ:
В диэлектрике с удельной проводимостью γ создано однородное электрическое поле напряжённостью E = 2⋅104 В/м. Плотность тока в диэлектрике составляет δ = 2 мкА/м2. Найти мощность тепловых потерь в диэлектрике, если его объём составляет V = 20 см3. Ответ выразить в нВт.
Ответ:
Длинному металлическому цилиндру радиусом R = 10 см сообщили заряд на единицу длины, равный
Кл. Цилиндр поместили в бесконечную слабо проводящую среду с удельной проводимостью γ и диэлектрической проницаемостью ε = 40. Пренебрегая изменением заряда цилиндра и краевыми эффектами, найти удельную проводимость γ среды,
если плотность тепловой мощности, выделяющейся на расстоянии r = 50 см от оси цилиндра, равна p = 40 Вт/м3. Ответ выразить мСм/м.
Ответ:
Между электродами сферического конденсатора находится диэлектрик, удельная проводимость которого меняется в функции расстояния
от центра сферы по закону
, a = 10–4 См. Радиусы внутренней и внешней обкладок соответственно R1 = 1 см и R1 = 2⋅e см. Напряжение между электродами равно 
В. Определить ток утечки через несовершенную изоляцию. Ответ выразить в мА.Ответ:
Цилиндрический конденсатор с двухслойным диэлектриком имеет радиус внутренней обкладки, цилиндрической поверхности, разделяющей диэлектрики, и радиус внешней обкладки соответственно r1 = 2 см, r2 = 6 см, r3 = 18 см, удельные проводимости слоёв γ1 = 2⋅10–8 См/м, γ2 = 8⋅10–8 См/м. Длина конденсатора
см. Определить проводимость утечки через изоляцию конденсатора (можно воспользоваться аналогией с электростатическим полем). Ответ записать в нСм.Ответ:
Тангенциальная составляющая вектора плотности тока в первой среде равна
А/м2. Угол α1 = 60°. Определить величину плотности тока δ2 во второй среде, если γ1 = 2⋅107 См/м; γ2 = 5⋅107 См/м. Ответ выразить в МА/м2.
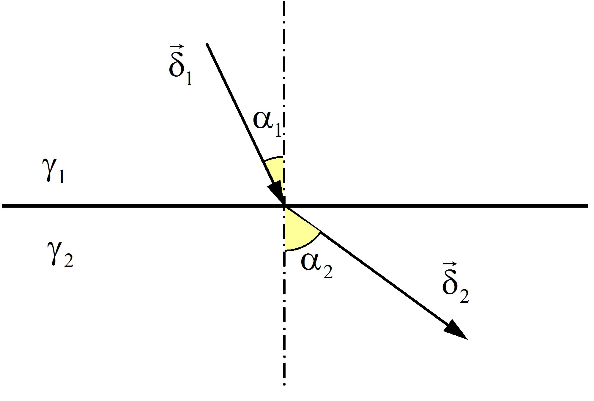
Ответ:
В диэлектрике с удельной проводимостью γ создано электрическое поле. Найти удельную мощность тепловых потерь в данной точке диэлектрика, если в этой точке напряжённость электрического поля равна E = 2⋅104 В/м, а плотность электрического тока δ = 2 мкА/м 2. Ответ выразить в мВт/м3.
Ответ:
Шаровой заземлитель радиусом R = 0,5 м находится на значительной глубине (влиянием поверхности земли пренебрегаем). Через заземлитель протекает ток I = 1000⋅π А. Определить плотность тока δ на расстоянии r = 4 м от центра заземлителя. Ответ выразить в мА/м2.
Ответ:
В диэлектрике с удельной проводимостью γ создано электрическое поле напряжённостью E = 2⋅104 В/м. Найти плотность электрического тока δ в данной точке диэлектрика, если известна удельная мощность тепловых потерь в этой точке p = 36 мВт/м3. Ответ выразить в нА/м2.
Ответ:
Два провода, имеющие одинаковые площади поперечного сечения S, но различные удельные сопротивления ρ1 = 2⋅10–8 Ом·м и ρ2, соединены встык. По проводникам течёт ток
А. Величина заряда, возникшего в сечении стыка, равна q = 10⋅10–18 Кл. Найти удельное сопротивление 2-го проводника ρ2, если нормальная составляющая напряжённости электрического поля на поверхности раздела проводников удовлетворяет условию 
. Ответ записать в нОм·м.Ответ:
Металлическому шару радиуса R = 10 см сообщили заряд
Кл. Шар поместили в бесконечную слабо проводящую среду с удельной проводимостью γ и диэлектрической проницаемостью ε = 40. Пренебрегая изменением заряда шара, найти удельную проводимость γ среды, если плотность тепловой мощности, выделяющейся на расстоянии r = 50 см от центра шара, равна
p = 40 Вт/м3. Ответ выразить мСм/м.
Ответ:
ПРОМЕЖУТОЧНЫЙ ТЕСТ 2
Квадратная рамка с током А и числом витков находится в магнитном поле с индукцией мкТл. Сторона рамки м. Вектор магнитной индукции параллелен плоскости рамки и составляет с двумя противоположными сторонами рамки угол Определить момент сил, действующих на рамку со стороны магнитного поля, относительно оси, проходящей через середины двух противоположных сторон рамки, которые параллельны вектору . Ответ выразить в мкН•м.
Ответ:
По бесконечному прямому проводу течёт ток . Индукция магнитного поля вне провода на расстоянии м от его оси равна мкТл. Найти ток , текущий по проводу.
Ответ:
По двум бесконечным параллельным проводам текут одинаковые токи. Расстояние между проводами м. Сила взаимодействия между проводами на единицу длины провода равна Н / м. Определить величину тока в проводах.
Ответ:
Бесконечный провод с током А находится в магнитном поле с индукцией мкТл. Угол между вектором магнитной индукции и направлением тока . Определить силу, действующую на единицу длины провода. Ответ выразить в мН / м.
Ответ:
По бесконечному прямому проводу течёт ток
. Напряжённость магнитного поля вне провода на расстоянии м от его оси равна 
А / м. Найти ток , текущий по проводу.Ответ:
По бесконечному прямому проводу течёт ток А. Определить напряжённость магнитного поля вне провода на расстоянии м от его оси.