ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт финансов, экономики и управления
| (наименование института полностью) |
| Управление персоналом |
| (Наименование учебного структурного подразделения) |
| 38.03.03 |
| (код и наименование направления подготовки / специальности) |
| Управление персоналом |
| (направленность (профиль) / специализация) |
Практическое задание №1
по учебному курсу « Экономика »
(наименование учебного курса)
Вариант ____ (при наличии)
| Обучающегося | А.Е. Калиткина | |
| | (И.О. Фамилия) | |
| Группа | УПбвд-2101а | |
| | | |
| Преподаватель | Ю. А. Анисимова | |
| | (И.О. Фамилия) | |
Тольятти 2023
Задача 1.
Метод точечной эластичности используется в том случае, когда выведена функциональная связь рассматриваемых факторов (например, функция спроса от цены или предложения) и необходимо оценить их взаимную чувствительность в конкретной ситуации (в точке). Эта зависимость характеризует относительное изменение одного фактора (например, объема спроса) при бесконечно малом изменении другого фактора (например, цены):
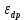 = Q'(P) *
= Q'(P) * 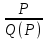 ,
,где
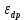 - коэффициент эластичности спроса;
- коэффициент эластичности спроса;Q'(P) - производная функции спроса по цене;
Р - цена;
Q(P) - величина спроса при данной цене
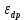 = (3 – Р)' *
= (3 – Р)' * 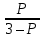 = - 2
= - 2 -1*Р = -2*(3-Р)
3Р = 6
Р = 2 ден.ед.
Ответ : значение цены товара равно 2 ден.ед.
Задача 2.
В условиях рынка ситуация стремится к равновесию в результате того, что ищется такое положение, которое устраивает и продавцов и покупателей. Это достигается в точке пересечения кривых спроса и предложения. А так как кривые представлены соответствующими функциями, то эта точка соответствует равенству функций спроса и предложения.
Поэтому приравняем функции спроса и предложения и найдем координаты этой точки.
Qd = Qs
120–2*Р = 3*Р-100
5*Р = 220
Р = 44 руб. (это равновесная цена)
Подставляем равновесную цену в любую из функций :
Q = 120 – 2*44 = 32 ед. (это равновесный объем).
Налоги на продавцов являются неценовым фактором предложения, т.к. налоги влияют на прибыль продавцов и для того, чтобы компенсировать рост налогов, производители увеличивают цену продукции. Продавцы рассматривают налоги как дополнительные издержки, что при прочих равных условиях означает сокращение предложения, которое вызывает смещение кривой предложения на величину налога.
Функция спроса останется прежней :
Qd = 120–2*Р
А функция предложения из-за налога сдвинется и будет иметь вид:
Qs = 3(P – 10) - 100 = 3Р – 130.
Приравняв функции спроса и предложения найдем новую (с учетом налога) равновесную цену.
120–2*Р = 3*Р-130
5*Р = 250
Р = 50 руб. (это равновесная цена)
Подставляем равновесную цену в любую из функций :
Q = 120 – 2*50 = 20 ед.
Найдем :
– эластичность предложения в точке равновесия и после введения налога
Метод точечной эластичности используется в том случае, когда выведена функциональная связь рассматриваемых факторов (например, функция спроса от цены или предложения) и необходимо оценить их взаимную чувствительность в конкретной ситуации (в точке). Эта зависимость характеризует относительное изменение одного фактора (например, объема предложения) при бесконечно малом изменении другого фактора (например, цены):
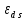 = Q'(P) *
= Q'(P) *  ,
,где
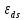 - коэффициент эластичности предложения;
- коэффициент эластичности предложения;Q'(P) - производная функции предложения по цене;
Р - цена;
Q(P) - величина предложения при данной цене
в точке равновесия :
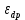 = (3Р-100)' *
= (3Р-100)' * 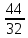 = 4,125
= 4,125 после введения налога :
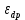 = (3Р-130)' *
= (3Р-130)' * 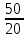 = 7,5
= 7,5 – излишек продавца, излишек покупателя и общественное благосостояние
Qd = 120 - 2*Р = 0
Pмакс = 60 руб.
Qs = 3*Р-100 = 0
Pмин = 3,33 руб.
Определим цену при старой функции предложения и новом объеме.
20 = 3Р-100
Р3 = 40
Излишек продавца до налога = ½ * (44 – 3,33) * 32= 650,72 руб.
Излишек продавца после введения налога = ½ * (44 – 40) * 20 = 40 руб.
Излишки покупателя до налога = ½ * (60 – 44) * 32 = 256 руб.
Излишки покупателя после введения налога = ½ * (60 – 50) * 20 = 100 руб.
Определим изменение общественного благосостояния.
Часть потерь продавцов и покупателей никто не получил, это чистые потери общества (потери «мертвого груза»), они возникают по причине того, что налог ведет сокращению объема производства.
Потери «мертвого груза» = ½ * (Р2 – Р1) * (Q1 - Q2) + ½ * (Р1 – Р3) * (Q1 - Q2) = ½ * (50 – 44) * (32 – 20) + ½ * (44 – 40) * (32 – 20) = 36 + 24 = 60 руб.
– величину дохода государства после введения налога в размере
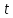 руб.
руб.Определим, каков доход государства от введения этого налога.
Налог = Ставка налога * Новый равновесный объем
Налог = 10 * 20 = 200 руб.
– распределение налогового бремени между продавцами и покупателями (в процентах), сумму налога, выплаченную покупателями и продавцами
Непосредственными плательщиками в государственный бюджет этих налогов являются обычно продавцы. Ставки потоварного налога устанавливаются либо в определенном проценте от цены товара, либо в абсолютной сумме (в рублях) с каждой единицы товара. Обратим внимание на следующий факт. Несмотря на то, что весь налог вносится в госбюджет продавцами
, часть «налогового бремени» ложится на покупателей.
Распределение налогового бремени между покупателями и продавцами зависит от соотношения наклонов линий спроса и предложения, а следовательно, от эластичности спроса и предложения.
Определим налоговое бремя на покупателей :
(Р2 – Р1) * Q2 = (50 – 44) * 20 = 120 руб.
120/200 * 100% = 60%
Определим налоговое бремя на продавцов :
(Р1 – Р3) * Q2 = (44 – 40) * 20 = 80 руб.
80/200 * 100% = 40%
Проиллюстрируем графически рыночное равновесие до введения налога и после.
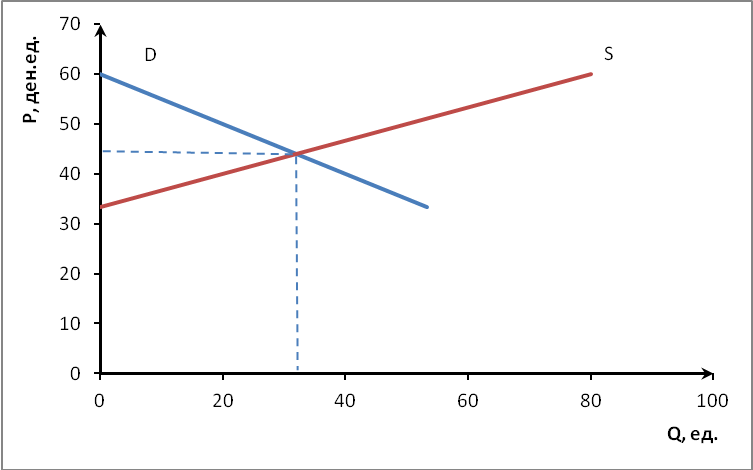
Рисунок 1 – Рыночное равновесие до введения налога
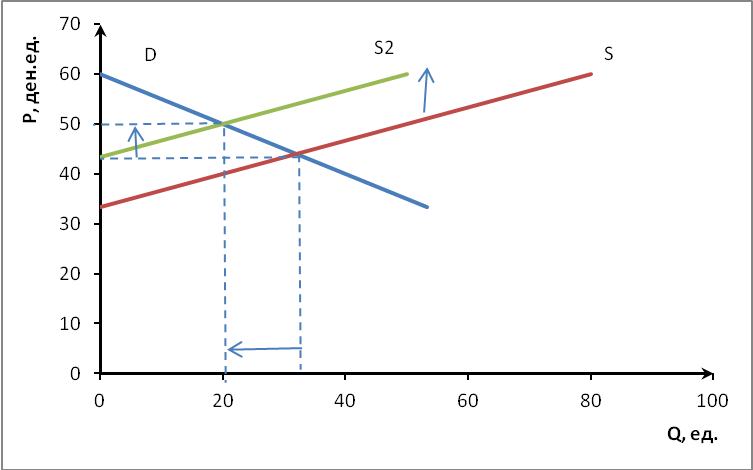
Рисунок 2 – Изменение рыночного равновесия после введения налога
Задача 3.
Так как имеются данные только о цене товара Х, то найдем количество товара Х, если весь доход направляется только на покупку его.
Предельная норма замены - норма, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя.
Предельная норма замены - это мера, показывающая максимальное количество товара, от которого потребитель отказывается ради получения одной дополнительной единицы другого товара :
MRS = ∆X / ∆Y.
Найдем сколько единиц товара Х прибавиться, если полностью отказаться от покупки товара Y :
MRS = ∆X / (16-0) = 0,5
∆X = 8 ед.
Определим максимальное количество товара Х при данном доходе :
Х = 8 + 8 = 16 ед.
Учитываем, что доход полностью израсходован :
XPx + YPy + …и т.д. = I
где X, Y и т.д. - виды товаров;
Рх, РY - цена этих товаров;
I - бюджетный доход потребителя.
I = 16*5 = 80 ден.ед.
Ответ : доход потребителя равен 80 ден.ед.
З
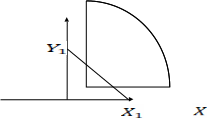 адача 4. На рисунке представлены кривая безразличия и бюджетная линия некоего потребителя (значения для варианта выбираются из таблицы 1.5).
адача 4. На рисунке представлены кривая безразличия и бюджетная линия некоего потребителя (значения для варианта выбираются из таблицы 1.5).
Таблица 1.5
Количество товара
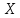 и Y, цена товара и значение
и Y, цена товара и значение
| Вариант | Количество 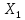 , ед. , ед. | Количество 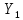 , ед. , ед. | Цена товара 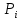 , руб. , руб. |
| 7 | 30 | 50 | Цена товара X: 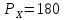 |
Необходимо определить:
– наклон бюджетной линии (
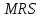 );
);– доход (бюджет) потребителя, если цена товара равна
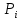 руб.
руб.Выпишите уравнение бюджетной линии.
Решение
Определим:
– наклон бюджетной линии (
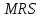 )
)Точки А(0, 50) и В(30, 0)
а) Найдем угловой коэффициент:
m = (yB - yA)/ (xB - xA)
m = (0 – 50) / (30 – 0) = - 5/3
MRS = -1,667
Выпишем уравнение бюджетной линии
б) Подставим угловой коэффициент и координаты точки А в формулу
y - yA = m×(x - xA)
у – 50 = - 1,667 (х – 0)
у = - 1,667 х + 50
Уравнение бюджетной линии : Y = - 1,667*Х + 50
– доход (бюджет) потребителя, если цена товара равна
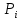 руб.
руб.Так как имеются данные только о цене товара Х, то рассматриваем вариант, если весь доход направляется только на покупку его.
Учитываем, что доход полностью израсходован :
XPx + YPy + …и т.д. = I
где X, Y и т.д. - виды товаров;
Рх, РY - цена этих товаров;
I - бюджетный доход потребителя.
I = 30*180 = 5400 руб.
Ответ : наклон бюджетной линии (
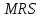 ) равен -1,667, доход (бюджет) потребителя равен 5400 руб., уравнение бюджетной линии Y = - 1,667*Х + 50.
) равен -1,667, доход (бюджет) потребителя равен 5400 руб., уравнение бюджетной линии Y = - 1,667*Х + 50.