Файл: Занятие Методика изучения курса математики в старших классах средней школы (1011 классы). Блоки алгебра, начала анализа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 54
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, чтобы про любой объект можно было сказать, входит он, или не входит, в объем рассматриваемого понятия. Раскрытие содержания понятия в указанном смысле называется его определением. Это можно осуществить разными способами. Один из способов определения понятия называется «определение через ближайший род и видовые отличия».
Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.
Определить понятие – это значит дать способ, позволяющий отделить объекты, охватываемые данным понятием, от всех других объектов изучения в зависимости от присущих им существенных свойств. Таким образом, определение (лат. «definitio» – «определение») понятий – логическая операция, в процессе которой раскрывается содержание понятия.
Определение понятий – это логическая операция, с помощью которой указываются существенные (отличительные) свойства объекта изучения, достаточные для распознавания этого объекта, т.е. в процессе которой раскрывается содержание понятия либо устанавливается значение термина.
Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.
По способу раскрытия свойств определяемого понятия различают неявные и явные определения. К неявным определениям относятся невербальные определения, к явным - вербальные определения (лат. слово «verbalis» означает «словесный»).
Невербальное определение – это определение значения понятия путём непосредственной демонстрации предметов или указания контекста, в котором применяется то или иное понятие.
Невербальные определения понятий используются в начальном курсе математики, так как младшие школьники обладают преимущественно наглядным мышлением, и именно наглядные представления о математических понятиях играют для них основную роль в обучении математике.
Невербальные определения разделяются на остенсивные (лат. слово «ostendere» – «показывать») и контекстуальные определения.
Остенсивное определение – определение, в котором содержание нового понятия раскрывается путём демонстрации объектов (указания на объекты).
Анализ - логический прием, с помощью которого изучаемый предмет мысленно расчленяется на части, каждая из которых затем рассматривается отдельно. В случае необходимости эти части в свою очередь опять могут быть расчленены на другие части и т.д., следовательно процедура разложения целого на части производится до получения элементарных и уже известных предметов.
В мыслительной деятельности человека анализ и синтез, как два противоположных по ходу движения мысли рассуждения, дополняют друг друга. Если с помощью анализа определяются пути решения поставленного вопроса, то с помощью синтеза это решение осуществляется. Рассмотрим применение анализа и синтеза на конкретных примерах.
Используя анализ, сначала учащиеся должны разбить (мысленно, в худшем случае линейкой) эти фигуры на два треугольника и потом подобрать необходимые треугольники. Учитель при этом должен обратить внимание на то, что для ответа на поставленный вопрос сначала фигуры разбиваем на части, а потом их снова соединяем, т.е. делаем обратное действие.
При их использовании анализа и синтеза учителю рекомендуется на первый план выдвинуть процедуру разбиения на части (анализ) и затем объединения частей (синтез) предметов.
Анализ и синтез присутствуют во всех логических операциях. Очень широко они применяются при решении задач, когда ход рассуждений называют: "аналитический метод разбора" и "синтетический метод разбора".
В процессе умственной работы приходится делать и обратную мыслительную операцию: отдельные части или элементы, полученные при анализе, соединять в целое. Логический прием объединения отдельных элементов или частей в целое, обогащенное новыми знаниями, называется синтезом.
Познавая окружающий мир, человек устанавливает различные отношения: между объектами, между объектами и их свойствами. Взаимосвязи между объектами и свойствами выражаются с помощью предложений. Предложения могут быть сформулированы при помощи слов и записаны при помощи математических символов: «У квадрата все стороны равны»; «5 7».
Среди предложений выделяют высказывания и высказывательные формы (предикаты).
Рассмотрим теперь теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник - равнобедренный». Оно, как известно, истинное и поэтому является теоремой. Ее называют
теоремой, обратной данной.
Замечание. В том случае, если предложение, обратное данному, будет истинно, его называют теоремой, обратной данной.
Замечание. Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не А, то не В», которое называют противоположным данному.
Но не всегда это предложение является теоремой. Например, предложение, противоположное теореме «если четырехугольник является прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
Замечание. В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Таким образом, если для теоремы А В сформулировать обратное или противоположное предложения, то их надо доказывать (и тогда их можно называть соответственно обратной и противоположной теоремами) или опровергать.
Замечание. Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не В, то не А», которое называют обратным противоположному.
Например, для теоремы «если четырехугольник является прямоугольником, то в нем диагонали равны» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он (четырехугольник) не является прямоугольником». Это, как известно, предложение истинное и, следовательно, является теоремой. Ее называют обратно противоположной данной.
Замечание. Для какой бы теоремы мы ни формулировали предложение обратное противоположному, оно всегда будет теоремой, потому имеется следующая равносильность (А В) (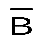
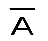 ).
).
Эту равносильность называют законом контрапозиции. Мы принимаем его без доказательства. Согласно этому закону,
Закон контрапозиции. Предложение, обратно противоположное какой-либо теореме, также является теоремой, и, значит, вместо данной теоремы можно доказывать теорему, обратно противоположную данной.
Необходимыми условиями правильности утверждения А называются такие условия, без соблюдения которых утверждение А заведомо не может быть верным, а достаточными условиями правильности утверждения А называются условия, при выполнении которых утверждение А заведомо верно.
Теорема – это мат - ое предложение, истинность которого устанавливается посредством доказательства (рассуждения)
2 Вида формулирования теоремы
Всегда можно из одного вида формулирования теоремы перейти в другой. Если теорема сформулирована в условной форме, то в ней должно быть ясно указан при каких условиях рассматривается в ней тот или иной объект (условие) и что в этом объекте утверждается (заключение теоремы).
Пример:
Теорема: В параллелограмме диагонали, пересекаясь, делятся пополам.
Если четырехугольник – параллелограмм, то…
Условие Р четырехугольник – параллелограмм, диагонали его пересекаются
Заключение G точка пересечения диагоналей делит каждую из них пополам.
Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т.е., приняв, что Р истинно, соответствии с правилами вывода показать, что G истинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно целом.
Доказательство включает в себя три основных элемента:
Тезис (Главная цель доказательства – установить истинность тезиса). Форма выражения тезиса суждение.
Аргументы (основание) доказательства – положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.
Демонстрация – логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.
При изучении теорем школьного курса математики учитель придерживается следующей последовательности:
Самое большое различие между дедуктивным и индуктивным рассуждением состоит в том, что дедуктивное рассуждение начинается с утверждения или гипотезы, а затем проверяет, верно ли это через наблюдение, где индуктивные рассуждения начинаются с наблюдений и отходят назад к обобщениям и теориям
Задача – понятие неопределяемое, и в самом широком смысле означает то, что требует исполнения решения. В каждой задаче имеется условие – то, что дано, и требование – то, что надо найти, доказать, обосновать. Решить задачу – это значит выполнить ее требования. Текст задачи иногда называют ее фабулой. История свидетельствует, что математика как наука возникла из решения задач, развивалась и развивается через решение задач.
Задачи на уроках математики решаются в основном фронтальным образом. Фронтальное решение задач -решение одной и той же задачи всеми учениками класса в одно и то же время. Организация фронтального решения задач может быть различной.
-
Понятия. Способы определения понятий. Требования к определению понятий.
Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.
Определить понятие – это значит дать способ, позволяющий отделить объекты, охватываемые данным понятием, от всех других объектов изучения в зависимости от присущих им существенных свойств. Таким образом, определение (лат. «definitio» – «определение») понятий – логическая операция, в процессе которой раскрывается содержание понятия.
Определение понятий – это логическая операция, с помощью которой указываются существенные (отличительные) свойства объекта изучения, достаточные для распознавания этого объекта, т.е. в процессе которой раскрывается содержание понятия либо устанавливается значение термина.
Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.
По способу раскрытия свойств определяемого понятия различают неявные и явные определения. К неявным определениям относятся невербальные определения, к явным - вербальные определения (лат. слово «verbalis» означает «словесный»).
Невербальное определение – это определение значения понятия путём непосредственной демонстрации предметов или указания контекста, в котором применяется то или иное понятие.
Невербальные определения понятий используются в начальном курсе математики, так как младшие школьники обладают преимущественно наглядным мышлением, и именно наглядные представления о математических понятиях играют для них основную роль в обучении математике.
Невербальные определения разделяются на остенсивные (лат. слово «ostendere» – «показывать») и контекстуальные определения.
Остенсивное определение – определение, в котором содержание нового понятия раскрывается путём демонстрации объектов (указания на объекты).
-
Анализ в обучении математике. Применение анализа при поиске решения задач и доказательстве теорем.
Анализ - логический прием, с помощью которого изучаемый предмет мысленно расчленяется на части, каждая из которых затем рассматривается отдельно. В случае необходимости эти части в свою очередь опять могут быть расчленены на другие части и т.д., следовательно процедура разложения целого на части производится до получения элементарных и уже известных предметов.
В мыслительной деятельности человека анализ и синтез, как два противоположных по ходу движения мысли рассуждения, дополняют друг друга. Если с помощью анализа определяются пути решения поставленного вопроса, то с помощью синтеза это решение осуществляется. Рассмотрим применение анализа и синтеза на конкретных примерах.
Используя анализ, сначала учащиеся должны разбить (мысленно, в худшем случае линейкой) эти фигуры на два треугольника и потом подобрать необходимые треугольники. Учитель при этом должен обратить внимание на то, что для ответа на поставленный вопрос сначала фигуры разбиваем на части, а потом их снова соединяем, т.е. делаем обратное действие.
При их использовании анализа и синтеза учителю рекомендуется на первый план выдвинуть процедуру разбиения на части (анализ) и затем объединения частей (синтез) предметов.
Анализ и синтез присутствуют во всех логических операциях. Очень широко они применяются при решении задач, когда ход рассуждений называют: "аналитический метод разбора" и "синтетический метод разбора".
-
Синтез в обучении математике.
В процессе умственной работы приходится делать и обратную мыслительную операцию: отдельные части или элементы, полученные при анализе, соединять в целое. Логический прием объединения отдельных элементов или частей в целое, обогащенное новыми знаниями, называется синтезом.
-
Математические предложения. Теоремы, их виды. Необходимые и достаточные условия. Доказательство теорем. Виды доказательств.
Познавая окружающий мир, человек устанавливает различные отношения: между объектами, между объектами и их свойствами. Взаимосвязи между объектами и свойствами выражаются с помощью предложений. Предложения могут быть сформулированы при помощи слов и записаны при помощи математических символов: «У квадрата все стороны равны»; «5 7».
Среди предложений выделяют высказывания и высказывательные формы (предикаты).
Рассмотрим теперь теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник - равнобедренный». Оно, как известно, истинное и поэтому является теоремой. Ее называют
теоремой, обратной данной.
Замечание. В том случае, если предложение, обратное данному, будет истинно, его называют теоремой, обратной данной.
Замечание. Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не А, то не В», которое называют противоположным данному.
Но не всегда это предложение является теоремой. Например, предложение, противоположное теореме «если четырехугольник является прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».
Замечание. В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Таким образом, если для теоремы А В сформулировать обратное или противоположное предложения, то их надо доказывать (и тогда их можно называть соответственно обратной и противоположной теоремами) или опровергать.
Замечание. Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не В, то не А», которое называют обратным противоположному.
Например, для теоремы «если четырехугольник является прямоугольником, то в нем диагонали равны» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он (четырехугольник) не является прямоугольником». Это, как известно, предложение истинное и, следовательно, является теоремой. Ее называют обратно противоположной данной.
Замечание. Для какой бы теоремы мы ни формулировали предложение обратное противоположному, оно всегда будет теоремой, потому имеется следующая равносильность (А В) (
Эту равносильность называют законом контрапозиции. Мы принимаем его без доказательства. Согласно этому закону,
Закон контрапозиции. Предложение, обратно противоположное какой-либо теореме, также является теоремой, и, значит, вместо данной теоремы можно доказывать теорему, обратно противоположную данной.
Необходимыми условиями правильности утверждения А называются такие условия, без соблюдения которых утверждение А заведомо не может быть верным, а достаточными условиями правильности утверждения А называются условия, при выполнении которых утверждение А заведомо верно.
-
Прямое доказательство -
Индукция -
От противного -
Контрапозиция -
Построение -
Исчерпывание вариантов -
Биекция (Биективное доказательство – это техника доказательства, при которой находится биективная функция f : A → B между двумя конечными множествами A и B или сохраняющая размер биективная функция между двумя комбинаторными классами, чем доказывается одинаковость числа элементов, |A| = |B|) -
Двойной счёт
-
Методика изучения теорем. Примеры.
Теорема – это мат - ое предложение, истинность которого устанавливается посредством доказательства (рассуждения)
2 Вида формулирования теоремы
-
Условная -
Категорическая
Всегда можно из одного вида формулирования теоремы перейти в другой. Если теорема сформулирована в условной форме, то в ней должно быть ясно указан при каких условиях рассматривается в ней тот или иной объект (условие) и что в этом объекте утверждается (заключение теоремы).
Пример:
Теорема: В параллелограмме диагонали, пересекаясь, делятся пополам.
Если четырехугольник – параллелограмм, то…
Условие Р четырехугольник – параллелограмм, диагонали его пересекаются
Заключение G точка пересечения диагоналей делит каждую из них пополам.
Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т.е., приняв, что Р истинно, соответствии с правилами вывода показать, что G истинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно целом.
Доказательство включает в себя три основных элемента:
Тезис (Главная цель доказательства – установить истинность тезиса). Форма выражения тезиса суждение.
Аргументы (основание) доказательства – положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов - суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.
Демонстрация – логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.
При изучении теорем школьного курса математики учитель придерживается следующей последовательности:
-
Постановка вопроса (создание проблемной ситуации) -
Обращение к опыту учащихся -
Высказывание предположения -
Поиск возможных путей решения -
Доказательство найденного факта -
Проведение доказательства в максимальной форме -
Установление зависимости доказанной теоремы от ранее известных.
-
Индукция и дедукция. Их использование на уроках математики.
Самое большое различие между дедуктивным и индуктивным рассуждением состоит в том, что дедуктивное рассуждение начинается с утверждения или гипотезы, а затем проверяет, верно ли это через наблюдение, где индуктивные рассуждения начинаются с наблюдений и отходят назад к обобщениям и теориям
-
Задачи в обучении математике. Функции задач в школьном курсе математики. Классификация школьных математических задач.
Задача – понятие неопределяемое, и в самом широком смысле означает то, что требует исполнения решения. В каждой задаче имеется условие – то, что дано, и требование – то, что надо найти, доказать, обосновать. Решить задачу – это значит выполнить ее требования. Текст задачи иногда называют ее фабулой. История свидетельствует, что математика как наука возникла из решения задач, развивалась и развивается через решение задач.
Задачи на уроках математики решаются в основном фронтальным образом. Фронтальное решение задач -решение одной и той же задачи всеми учениками класса в одно и то же время. Организация фронтального решения задач может быть различной.