Факультет экономики и финансов

Кафедра ______________________________________________________

Направление подготовки/Специальность ___________________________

Рейтинговая работа

по дисциплине___«Бухгалтерский учет и анализ 2»___

Задание/вариант № ___________________Ц______________________


Выполнена обучающимся _________________________

(№ группы, фамилия, имя, отчество)

Преподаватель ____________________________________________________

(фамилия, имя, отчество)

Москва – 2022 г
Задание 1
Используя ретроспективные данные за 6 лет, спрогнозируйте объем производства продукции на следующие 3 года при условии сохранения тенденций функционирования бизнеса.
Решение:

Таблица 1 - Исходные данные для трендового анализа

Период, г., x	2011	2012	2013	2014	2015		2016
Объём, шт., Y	78	83	87	91	95		99
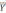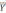= ΣYt / n = (78 + 83+87+91+95+99)/6 = 88,833						89

На основании представленной совокупностинаходим среднее значение ряда динамика. Для этого используем среднюю арифметическую,так как для оценки используется единичный ряд изменения показателей.

На рисунке 1 представлено изменение показателей и выявлена линия тренда.



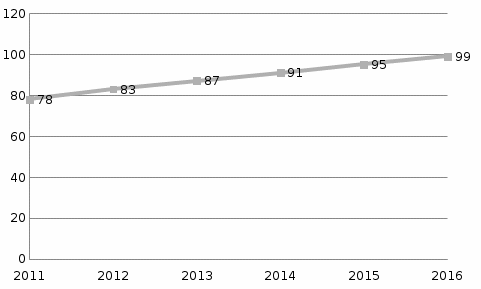
Рисунок 1 – Динамика выпуска продукции, штуках
Данный показатель говорит о том, что в среднем в течение 2011-2016гг. предприятие производило 88единиц продукции. Можно отметить, что объем производства увеличивается с каждым годом. Поэтому зависимость между факторным и результативным показателями носит прямолинейный характер. А для оценки используется уравнение парной регрессии:

---

Y_t= a + b*x

где а – свободный член уравнения при х = 0;

x – фактор, определяющий уровень изучаемого результативного показателя (независимый параметр);

b – коэффициент регрессии при факторном показателе; он характеризуют уровень влияния фактора на результативный показатель в абсолютном выражении.

Значение коэффициентов a и b найдем из системы уравнений, полученных по способу наименьших квадратов (x = t):



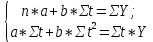
где n – число наблюдения;

t – независимый параметр;

Y – объём производства продукции.

Подставив полученные значения в систему уравнений, получим:



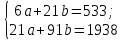
Умножим все члены первого уравнения на 21, а второго на 6. Затем проведем для сокращения системы и получим новую систему уравнений:



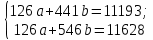
Из второго уравнения вычтем первое и определим показатели a и b:

546b-441b = 11628-11193

105b = 435

b = 435 / 105

b = 4,1



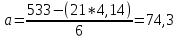
Уравнение связи для определения объёма производства в зависимости от периода времени при заданных данных имеет вид:

Y_x = 74,37+4,1*t.

Если в уравнение регрессии Y_x=74,3+4,1*t подставлять соответствующее значение t, то можно рассчитать прогнозируемое значение объёма производства (Y_x) для каждого ретроспективного года:
Y₂₀₁₁ =74,3+4,1* 1 = 78,8шт.

Y₂₀₁₂ =74,3+4,1* 2 = 82,6 шт.

Y₂₀₁₃ =74,3+4,1* 3 = 86,8 шт.

Y₂₀₁₄ =74,3+4,1* 4 = 90,9 шт.

Y₂₀₁₅ =74,3+4,1* 5 = 95,1шт.

Y₂₀₁₆ =74,3+4,1* 6 = 99,2шт.

Также делаем расчет и для прогнозных лет:
Y₇ = 74,3+4,1* 7 = 103,3 шт.

Y₈ = 74,3+4,1* 8 = 107,5 шт.

Y₉ = 74,3+4,1* 9 = 111,6 шт.

Значения Σt, ΣY, Σt², ΣtY рассчитаем на основании фактических исходных данных; результаты расчётов представим в таблице 2.
Таблица 2 – Расчёт показателей трендовой модели для прогноза объёма производства продукции

t	Y		Y*t	t2	Y2		Yt		Y-Yt	(Y-Yt)2
1	2		3	4	5		6		7	8
1	78		78	1	6084		78,48		-0,48	0,23
2	83		166	4	6889		82,62		0,38	0,15
3	87		261	9	7569		86,76		0,24	0,06
4	91		364	16	8281		90,90		0,10	0,01
5	95		475	25	9025		95,05		-0,05	0,00
6	99		594	36	9801		99,19		-0,19	0,04
Итого:
21	533		1938	91	47649		533		х	0,48
Среднее значение производства продукции = 533/ 6										88,8
Уравнение связи для определения прогнозного значения объёма производства Yx = 84,7+4,1*t.
Прогнозные значения объёма производства для последующих 3-х лет
7		84,7+4,1*7				103,3		Х
8		84,7+4,1*8				107,5		Х
9		84,7+4,1*9				111,6		Х
Среднеквадратическое отклонение:	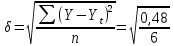									0,28
Коэффициент вариации: 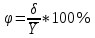. 0,28 / 88,8 *100%										0,32
Прогнозируемый диапазон изменения объёма производства для каждого квартала:
2017 год
от 103 шт. (103,3 – 0,28)										103
до 104 шт. (103,3+ 0,28)										104
2018 год
от 107 шт. (107,5 – 0,28)										107
до 108 шт. (107,5 + 0,28)										108
2019 год
от 111 шт. (111,6 – 0,28)										111
до 112 шт. (111,6 + 0,28)										112

---

Для оценки качества данных, определения диапазона изменения прогнозируемого объёма производства в каждый год необходимо рассчитать среднее квадратическое отклонение прогнозируемого показателя и коэффициент вариации.

Среднеквадратическое отклонение составило 0,28 шт. С учетом этого показателя определяем прогнозируемый диапазон изменения объема производства для каждого из трех лет, начиная с 2017 года.

Результаты расчетов показывают, что прогнозируемый диапазон объема производства составит:

для 2017 года – от 103 шт. до 104 шт.;

для 2018 года – от 107шт. до 108 шт.;

для 2019 года – от 111 шт. до 112шт.

В статистике принято, что, если коэффициент вариации

меньше 10%, то степень рассеивания данных считается незначительной,

от 10% до 20% - средней,

больше 20% и меньше или равно 33% - значительной,

значение коэффициента вариации не превышает 33%, то совокупность считается однородной,

если больше 33%, то – неоднородной.

Значение коэффициента вариации составило 0,32%, менее 10% степень рассеивания данных считается незначительной, низкая колеблемость анализируемого признака. Поэтому можно сделать вывод о точности прогноза. Производственный риск низкий, отклонение выработки продукции от рассчитанных данных не существенно.

Задание 2
Используя данные произвести факторный анализ следующих факторных детерминированных моделей.

1. Произвести расчет влияния факторов в четырёхфакторной мультипликативной модели ВП = ЧР * Д * П * ЧВ методом цепных постановок.

Таблица 3–Исходные данные анализа

Показатель	Условное обозначе- ние	2015г.	2016г.
Объём продукции, тыс. руб.	ВП	-	-
Среднесписочное число рабочих, чел.	ЧР	13	17
Количество отработанных дней одним рабочим за год, дн.	Д	256	260
Средняя продолжительность смены, ч.	П	8	8
Среднечасовая выработка одного рабочего, тыс. руб.	ЧВ	0,3	0,35

---

Решение:

Метод цепных подстановок основывается на том, что каждый фактор изменяется на последующее значение значение.

Таблица 4 - Расчёт влияния факторов в четырёхфакторной мультипликативной модели методом цепных подстановок

Показатель	Условное обозначе- ние	Т0	Т1	Изменение
				±		%
Объем продукции, тыс. руб.	ВП	7987,2	12376	4388,8		54,95
Среднесписочное число рабочих, чел.	ЧР	13	17	4		30,77
Количество отработанных дней одним рабочим за год, дн.	Д	256	260	4		1,56
Средняя продолжительность смены, ч.	П	8	8	0		0,00
Среднечасовая выработка одного рабочего, руб.	ЧВ	0,3	0,35	0,05		16,67
Общее изменение валового выпуска продукции: ΔВП=ВП1-ВП0
Влияние факторов на изменение валового выпуска продукции
ВП0 = ЧР0*Д0*П0*ЧВ0 13*256*8*0,30					7987,2
ВП усл1 = ЧР1*Д0*П0*ЧВ0 17*256*8*0,30					10444,8
ВП усл2 = ЧР1*Д1*П0*ЧВ0 17*260*8*0,30					10608
ВП усл3 = ЧР1*Д1*П1*ЧВ0 17*260*8*0,30					10608
ВП 1 = ЧР1*Д1*П1*ЧВ1 17*260*8*0,35					12376
Изменение объёма продукции за счёт:
Изменения количества рабочих (ΔВПчр): ВП усл1 - ВП0					2457,6
Изменения количества отработанных дней одним рабочим за год (ΔВПд): ВП усл2 – ВП усл1					163,2
Изменения средней продолжительности смены (ΔВПп): ВП усл3 – ВП усл2					0
Изменения среднечасовой выработки одним рабочим (ΔВПчв): ВП 1 – ВП усл3					1768
Баланс факторов ∑ΔВПi					4388,8

---

При изменении численности с 13 человек до 17 человек получаем значение условного объема 1 1044,08 тыс. руб. Отклонение объема составило 2457,6 тыс. руб. При изменении количества дней с 256 до 160 отработанных в среднем одним работником получаем условный объемом выпуска продукции 2 - 10608 тыс. руб. Отклонение между вторым условным объемом и первым условным объем - 163,2 тыс. руб. Изменения рабочей смены нет, поэтому третий условный объем составляет 10608 тыс. руб., отклонение между объемам 0. При изменении средней выработки с 0,30 тыс. руб. на человека до 0,35 тыс. руб. получаем отчетное значение 12376 тыс. руб., так как больше факторов нет. Изменение отчетного объема и третьего условного объема 1768 тыс. руб. Путем сложения всех факторов получаем, что изменение объема составило 4388,8 тыс. руб. Наибольший рост за счет 2457,6 тыс. руб. за счет роста численности сотрудников.
2. Произвести расчет влияния факторов в мультипликативной четырёхфакторной модели ВП = ЧР * Д * П * ЧВ методом абсолютных разниц.

Метод абсолютных разниц в мультипликативную модель подставляются абсолютное изменение фактораслева на право.

Таблица 5 - Расчёт влияния факторов методом абсолютных разниц в мультпликативной модели

Показатель	Условное обозначе- ние	Т0	Т1	Изменение
				±		%
Объём продукции, тыс. руб.	ВП	7987,2	12376	4388,8		54,95
Среднесписочное число рабочих, чел.	ЧР	13	17	4		30,77
Количество отработанных дней одним рабочим за год, дн.	Д	256	260	4		1,56
Средняя продолжительность смены, ч.	П	8	8	0		0,00
Среднечасовая выработка одного рабочего, руб.	ЧВ	0,3	0,35	0,05		16,67
Общее изменение валового выпуска продукции: ΔВП=ВП1-ВП0
Влияние факторов на изменение объёма продукции
Изменение численности рабочих 4 * 256*8*0,30					2457,6
Изменение количества отработанных дней одним рабочим 17 * 4 *8 * 0,30					163,2
Изменение средней продолжительности смены 17* 260 * 0 * 0,30					0
Изменение среднечасовой выработки 17*260*8*0,05					1768
Баланс отклонений 2457,6+163,2+1768					4388,8

---

Смотрите также файлы

• Вопрос Метод фокусгруппы.docx

• Практика 2 Физическая культура.docx

• утверждаю согласовано.docx

• Практическая работа 1 Выполнил(а) (фио полностью, должность и место работы) Тема Особенности содержания обновленных фгос ооо, фгос соо.docx

• Лабораторная работа 1 по дисциплине (учебному курсу) Физика. Механика. Молекулярная физика.docx